Development leading to Bohr’s model of atom, class 11

In the past, when scientists studied how radiations interact with matter, they learned a lot about the structure of atoms and molecules. Neils Bohr used these findings to make Rutherford’s model better. There were two significant developments that played an essential role in the formulation of Bohr’s model of atom: They were:

1. Electromagnetic radiation has a dual character, behaving like both waves and particles.
2. Experimental observations about atomic spectra were also significant in shaping his model.

In this article, we will briefly discuss the development that lead to Bohr’s model of atom. So let’s get started…

Wave Nature of Electromagnetic Radiation

In the mid-nineteenth century, physicists studied the absorption and emission of radiation by heated objects, known as thermal radiation. They wanted to understand what thermal radiation consists of and found that it is composed of electromagnetic waves of different frequencies or wavelengths.

This concept was not known at the time. The active study of thermal radiation laws took place in the 1850s. In the early 1870s, James Clerk Maxwell developed the theory of electromagnetic waves and their emission by accelerating charged particles, later confirmed by Heinrich Hertz through experiments.

James Maxwell explained the interaction between charged bodies and the behavior of electrical and magnetic fields on a macroscopic level. He proposed that when an electrically charged particle moves under acceleration, it produces alternating electrical and magnetic fields, which are transmitted as waves known as electromagnetic waves or electromagnetic radiation.

Read Also:

• Maxwell’s equations class 12: integral form, differential form, applications, and explanation
• Displacement current class 12: definition, modification, formula, and properties
• Electromagnetic waves class 12: definition, equation, graphical representation, and applications
• Mathematical representation of electromagnetic waves, class 12
• Maxwell’s prediction of electromagnetic waves, class 12

The idea of light as a form of radiation has been known since ancient times, with speculation about its nature dating back to earlier periods. In the past, it was believed that light consisted of particles (corpuscles), but in the 19th century, the wave nature of light was established.

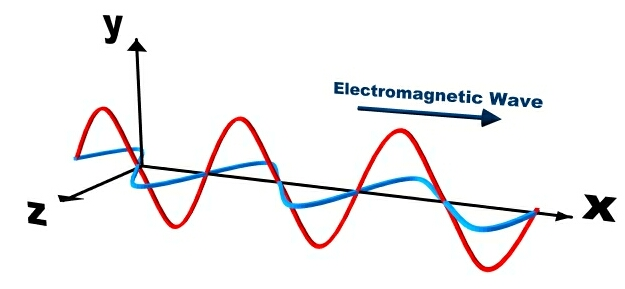
Maxwell was the first to discover that light waves are linked to oscillating electric and magnetic fields. Although these electromagnetic wave motions are complex in nature. Here, we will focus on some basic properties of electromagnetic wave motion.

Properties of electromagnetic wave motion

Some basic properties of electromagnetic wave motion are:

• Oscillating electric and magnetic fields: These waves consist of oscillating electric and magnetic fields that are perpendicular to each other and to the direction of wave propagation.
• Transverse waves: They are transverse waves, meaning the oscillations are perpendicular to the direction of the wave’s motion.
• Can travel through a vacuum: Electromagnetic waves do not require a medium to propagate. They have the ability to travel across a vacuum.
• Spectrum: The electromagnetic spectrum includes a wide range of waves, from radio waves with long wavelengths and low frequencies to gamma rays with short wavelengths and high frequencies.

Read Also:

• Difference between isobars and isotopes (Tabular form)
• Isobars and Isotopes: definition, examples, and differences, class 11
• Atomic number and atomic mass class 11
• Rutherford gold foil experiment class 11
• Drawbacks of Rutherford model of atom class 11

Properties of electromagnetic radiation

Here are some basic properties of electromagnetic waves:

1. Wave nature: Electromagnetic radiation is a form of energy that travels in the form of waves through space.
2. Electric and magnetic fields: These waves consist of oscillating electric and magnetic fields that are perpendicular to each other and to the direction of wave propagation.
3. Speed of light: Electromagnetic waves travel at the speed of light, approximately 299,792 kilometers per second (km/s) in a vacuum.
4. Transverse waves: They are transverse waves, meaning the oscillations are perpendicular to the direction of the wave’s motion.
5. Wavelength and frequency: Electromagnetic waves have various wavelengths and frequencies. Wavelength ($\lambda$) is the distance between successive wave crests, and frequency ($\nu$) is the number of wave cycles per second. The relation between the speed of light, wavelength, and frequency is given as $c=\nu\lambda$.
6. Wavenumber: The number of wavelengths per unit length is referred to as the wavenumber. Its units are m^-1 which is the inverse of wavelength. It is denoted by $\bar{v}$.
7. Spectrum: The electromagnetic spectrum includes a wide range of waves, from radio waves with long wavelengths and low frequencies to gamma rays with short wavelengths and high frequencies.
8. Interaction with matter: Electromagnetic waves can be absorbed, reflected, or transmitted when they interact with matter. This interaction gives rise to various phenomena, such as the colors of objects and the behavior of light in lenses and prisms.
9. Energy transmission: Electromagnetic waves carry energy from one place to another, and they are essential for various technologies, including radio and television communication, microwaves, and visible light used in everyday life.

Particle Nature of Electromagnetic Radiation

Some phenomena like diffraction and interference can be explained by the wave nature of electromagnetic radiation. However, there were certain observations that couldn’t be explained by the 19th-century electromagnetic theory (known as classical physics). These observations include: 1). Emission of radiation from hot objects (black-body radiation): When objects are heated, they emit light and heat. The classical theory couldn’t fully explain how this emission happened. 2). Photoelectric effect: When light strikes a metal surface, it can knock out electrons from the metal. The classical theory couldn’t explain why this happened and how the energy of the light affected the number of electrons emitted. 3). Variation of heat capacity of solids with temperature: The classical theory couldn’t fully explain how the heat capacity of solids changed as the temperature increased. 4). Line spectra of atoms, especially hydrogen: When elements are heated or excited, they emit light at specific colors (frequencies), creating line spectra. The classical theory couldn’t explain why each element’s line spectrum was unique and why hydrogen, in particular, had a distinctive pattern. These unexplained phenomena led to the development of a new theory called “quantum mechanics,” which was based on Max Planck’s Quantum Theory. Quantum mechanics successfully addressed these issues and became the foundation for modern physics

In addition to behaving like waves, electromagnetic radiation also shows particle-like behavior. This might sound a bit strange because we often think of particles as tiny solid objects, but in the world of physics, particles can sometimes act more like tiny packets of energy.

The particle nature of electromagnetic radiation is described using something called “photons.” Think of photons as tiny, weightless balls of energy that travel through space at the speed of light. When light is emitted or absorbed, it does so in discrete units called photons.

Now, here’s a simple way to imagine this: Imagine you have a stream of water flowing out of a hose. Instead of being a continuous stream, the water comes out in tiny, individual droplets. Each droplet is like a photon—a packet of water energy in this case.

Similarly, when you shine a flashlight, it emits light in the form of many tiny packets of energy called photons. These photons carry the energy of the light and travel through space until they interact with something, like our eyes or a surface. When they interact, they can be absorbed, reflected, or transmitted, causing different effects, such as heating an object or creating a sensation of sight.

So, the particle nature of electromagnetic radiation means that light and other forms of electromagnetic waves can behave like both continuous waves and tiny packets of energy (photons), depending on how they are observed or interact with matter. This concept is a fundamental part of understanding the behavior of light and how it interacts with the world around us.

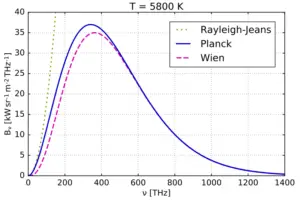
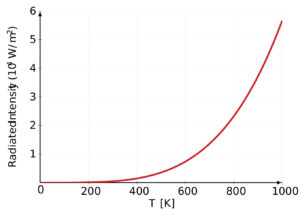
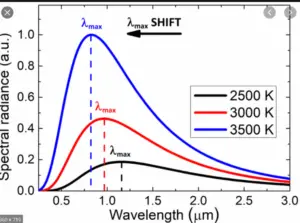
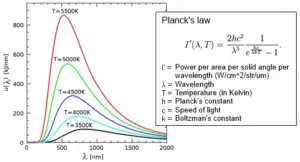
Planck’s Quantum Theory and Explanation for Black-Body Radiation

Read Also:

• Rutherford atomic model: postulates, observations, and limitations, class 11
• Thomson model of atom: postulates, drawbacks, & significance, class 11
• Cathode Tube Ray Experiment class 11: working, procedure, observation, and conclusion
• Discovery of Electron class 11: chemistry, NCERT
• Discovery of proton class 11: chemistry NCERT

Planck’s Quantum Theory

In the late 1800s, scientists were puzzled by the behavior of light and heat emitted by objects when they are heated up. Classical physics couldn’t fully explain these observations. Then, in 1900, Max Planck proposed his revolutionary idea that energy is emitted or absorbed by matter in discrete units or “packets” called “quanta” or “photons.” This means that energy is not continuously flowing, but rather it comes in specific amounts.

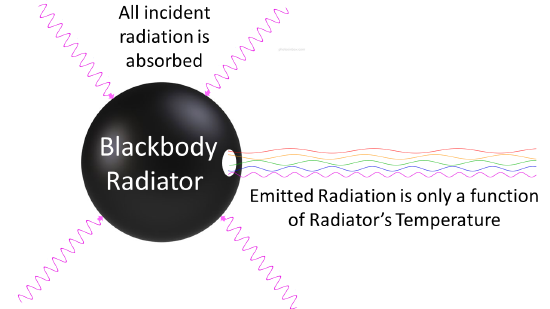
An explanation for Black-Body Radiation

Imagine you have a perfectly black object, like a black-painted box. When you heat this object, it starts to emit light and heat. This emission of light and heat is what we call “black-body radiation.” Classical physics couldn’t fully explain why this radiation behaved the way it did.

Planck’s breakthrough was to suggest that the energy of the radiation emitted by this black object (and all objects) is not continuous but comes in these tiny, discrete packets of energy, the “photons.” The energy of each photon depends on the frequency of the light it carries. Higher-frequency light has more energy per photon than lower-frequency light.

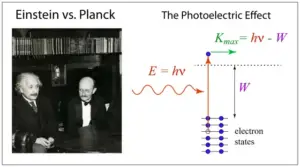
Planck’s theory provided a formula that related the energy of each photon to the frequency of the radiation. The formula is $E = h\nu$, where “E” is the energy of a photon, “h” is Planck’s constant (a very small number whose value is $6.626\times10^{–34} J s$), and “$\nu$” is the frequency of the radiation. This equation shows that the energy of a photon is directly proportional to its frequency.

By using his theory and this formula, Planck could accurately explain the distribution of light and heat emitted by a heated black object (black-body radiation), which classical physics had failed to do. This marked the birth of quantum mechanics, a new way of understanding the behavior of matter and energy at the smallest scales.

Planck’s Quantum Theory revolutionized physics and laid the foundation for modern quantum mechanics, which is now an essential part of our understanding of the universe at the atomic and subatomic levels.

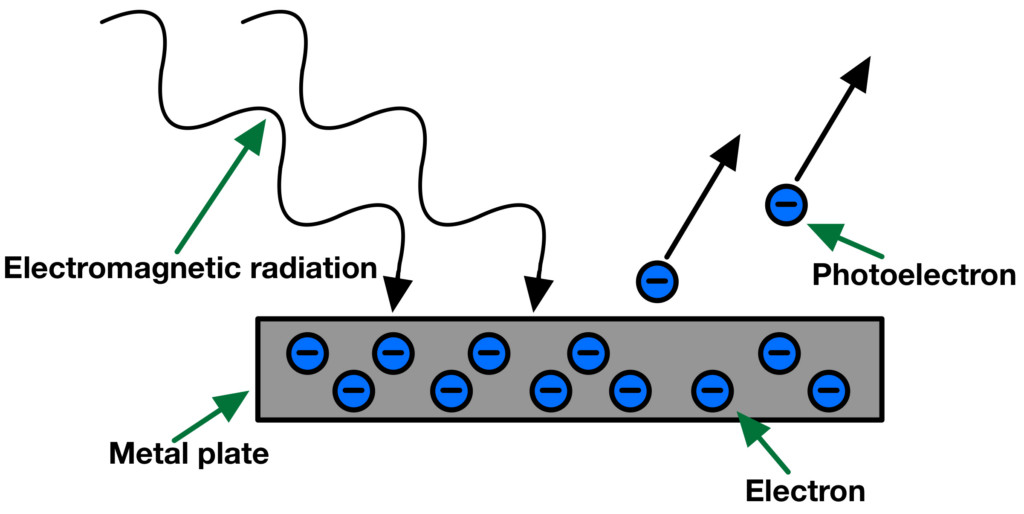
Explanation for the photoelectric effect

The photoelectric effect is a phenomenon where certain materials, typically metals, emit electrons when light (photons) of sufficient energy shines on their surface. This effect was first observed by German physicist Heinrich Hertz in 1887, and its detailed explanation was provided by Albert Einstein in 1905.

Key Observations

Here are the key observations of the photoelectric effect:

1. Instantaneous emission: When light of the appropriate frequency (or energy) strikes the metal surface, electrons are emitted immediately. There is no delay; it happens almost instantly.
2. Threshold frequency: Each metal has a specific minimum frequency of light below which no electrons are emitted, regardless of the light’s intensity. This minimum frequency is known as the threshold frequency.
3. Intensity-Independence: The number of electrons emitted depends on the intensity (brightness) of the light. However, the kinetic energy of the emitted electrons (their speed) is determined by the frequency (energy) of the light and remains constant, regardless of the light’s intensity.

Explanation

Albert Einstein’s explanation of the photoelectric effect was groundbreaking and required a shift from classical physics to the emerging field of quantum mechanics. Here’s a step-by-step explanation:

1. Photon Model of Light: Einstein proposed that light consists of tiny packets of energy called “photons.” Each photon carries a specific amount of energy, which is directly proportional to its frequency. High-frequency light has more energy per photon than low-frequency light.
2. Interaction with Electrons: When light (photons) shines on the metal surface, it interacts with the electrons in the metal. For an electron to be emitted, it must absorb one photon with enough energy to overcome the attractive forces holding it in the metal.
3. Threshold Frequency: The threshold frequency is the minimum frequency of light required to provide each electron with enough energy to escape the metal’s surface. Light with frequencies below the threshold frequency cannot supply enough energy for emission, regardless of its intensity.
4. Energy Conservation: Einstein showed that the energy of the photon ($E = h\nu$, where h is Planck’s constant and $\nu$ is the frequency) is entirely transferred to the electron during the photoelectric effect. If the photon’s energy ($h\nu$) is greater than the work function (the minimum energy needed to remove an electron from the metal), the excess energy becomes the kinetic energy of the emitted electron. $$E_{\text{photon}}​=\text{Work Function}+\text{Kinetic Energy of Electron}$$ $$h\nu = h\nu_0 +\frac{1}{2}m_e v^2$$
5. Instantaneous Emission and Conservation of Momentum: The photoelectric effect occurs instantaneously because, at the quantum level, energy and momentum are conserved. Electrons absorb a single photon and gain enough energy to break free from the metal almost instantly.

Significance of photoelectric effect

Einstein’s explanation of the photoelectric effect was a pivotal moment in the development of quantum mechanics. It provided strong evidence for the particle-like behavior of light and paved the way for our understanding of photons, quantum energy states, and the wave-particle duality of matter and light. The photoelectric effect also has practical applications in various technologies, such as photovoltaic cells (solar panels) and photoelectric sensors.

Dual Behavior Of Electromagnetic Radiation

The dual behavior of electromagnetic radiation refers to the fact that light and other forms of electromagnetic waves exhibit characteristics of both waves and particles. This duality was a revolutionary discovery in physics and lies at the heart of quantum mechanics.

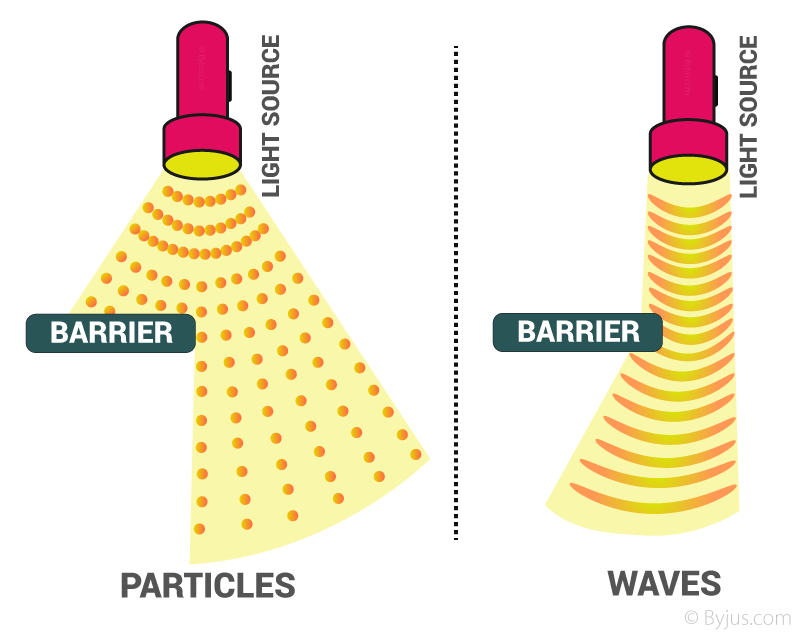
Wave-like Behavior

When we observe electromagnetic radiation as waves, it behaves in ways typical of waves:

1. Interference: Electromagnetic waves can interfere constructively (adding up) or destructively (canceling out) when they overlap, just like water waves.
2. Diffraction: Electromagnetic waves can bend and spread out when passing through small openings or around obstacles, similar to how waves bend around corners.
3. Wavelength and Frequency: Electromagnetic waves have different wavelengths and frequencies, which determine their colors (in the case of visible light) or properties like radio and microwave frequencies.

Particle-like Behavior

However, the dual nature of electromagnetic radiation also manifests as particle-like behavior:

1. Photoelectric Effect: When light shines on certain materials, it can knock out electrons from the material’s surface. This phenomenon cannot be explained by classical wave theory but can be understood using the concept of photons (particles of light).
2. Quantized Energy: Electromagnetic radiation (including light) comes in discrete energy packets called photons. The energy of a photon is directly proportional to its frequency, as described by Planck’s Quantum Theory.

Wave-Particle Duality

The duality of electromagnetic radiation implies that it doesn’t neatly fit into either the category of classical waves or classical particles. Instead, it displays characteristics of both, depending on the context and how it is observed or measured. This wave-particle duality is not limited to light; it is a fundamental feature of matter and energy at the quantum level.

Wave-particle duality was first proposed by Louis de Broglie and later confirmed through various experiments, such as the famous double-slit experiment, which demonstrated that light and other particles can create interference patterns like waves.

The discovery of wave-particle duality challenged classical physics and led to the development of quantum mechanics—a branch of physics that successfully describes the behavior of matter and energy at the atomic and subatomic scales. Quantum mechanics has since become an essential framework for understanding the fundamental nature of the universe.

Evidence for the quantized Electronic Energy Levels: Atomic spectra

The speed of light changes depending on the substance it passes through. So, when light moves from one material to another, it bends or changes direction. When we pass white light through a prism, it splits into different colors because each color has a different wavelength. The shorter the wavelength, the more the light bends.

When white light passes through a prism, it forms a beautiful colored band called a spectrum. This spectrum ranges from red (with the longest wavelength) to violet (with the shortest wavelength). The spectrum contains all the colors of the rainbow, merging smoothly from one color to the next. This kind of spectrum is called a continuous spectrum.

The visible spectrum we see ranges from violet to red. However, remember that visible light is just a small part of a larger group of electromagnetic radiation. This radiation interacts with matter (like atoms and molecules) in different ways. When matter absorbs energy from the radiation, its atoms and molecules become excited and move to a higher energy state. But these higher energy states are unstable, so to become stable again, they release energy by emitting radiation in various regions of the electromagnetic spectrum.

That’s why we see different types of radiation, like ultraviolet, infrared, and more, depending on the specific energy changes that happen when electromagnetic radiation interacts with matter. The colorful spectrum we see when light passes through a prism is just one example of how light and matter interact in fascinating ways.

Emission and Absorption Spectra

Emission and absorption spectra are two important concepts in the study of light and how it interacts with matter. Let’s explore it.

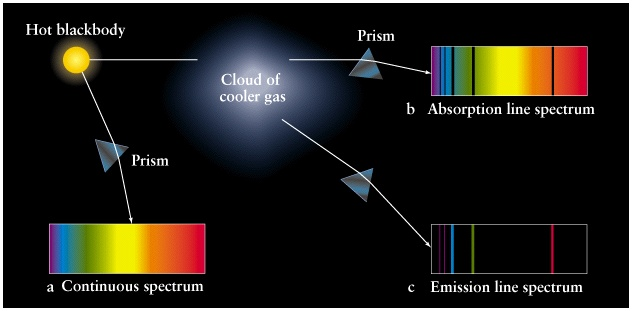
Emission Spectrum

An emission spectrum is produced when a substance emits light after being excited or energized. When energy is supplied to atoms or molecules (for example, by heating or passing an electric current through a gas), their electrons become excited and move to higher energy levels. These higher energy levels are unstable, and the electrons eventually return to their original, lower energy levels.

When the electrons return to their lower energy levels, they release the excess energy they gained as photons of light. Each electron releases a photon with a specific amount of energy, which corresponds to a particular color or wavelength of light. The collection of all these emitted photons creates the emission spectrum, which consists of distinct colored lines or bands.

The emission spectrum is unique to each element or substance. It acts like a fingerprint, helping scientists identify elements present in stars, gases, and other objects based on the colors they emit.

Absorption Spectrum

On the other hand, an absorption spectrum is created when light passes through a substance, and certain wavelengths are absorbed by the material. When light encounters atoms or molecules in the substance, some of its photons can be absorbed if their energy matches the energy required to move an electron to a higher energy level.

As the light passes through the substance, specific colors or wavelengths are “missing” from the transmitted light because those wavelengths were absorbed. The resulting spectrum shows dark lines or bands at these specific missing wavelengths, creating an absorption spectrum.

Just like an emission spectrum, the absorption spectrum is also unique to each element or substance. Scientists can use absorption spectra to identify the presence of elements in distant stars or to analyze the composition of various materials.

Relationship between Emission and Absorption Spectra

Interestingly, emission and absorption spectra are related. The colors or wavelengths that are emitted in the emission spectrum correspond precisely to the wavelengths that are absorbed in the absorption spectrum. The absorption spectrum acts as a “negative image” of the emission spectrum, showing the specific colors that were taken out (absorbed) from the initial light.

Emission and absorption spectra are crucial tools for understanding the behavior of light and matter and have practical applications in fields like astronomy, chemistry, and spectroscopy.

Read Also:

• Rutherford atomic model: postulates, observations, and limitations, class 11
• Thomson model of atom: postulates, drawbacks, & significance, class 11
• Cathode Tube Ray Experiment class 11: working, procedure, observation, and conclusion
• Discovery of Electron class 11: chemistry, NCERT
• Discovery of proton class 11: chemistry NCERT
• Discovery of Neutron class 11: history, properties, observations, and Conclusions
• Millikan oil drop experiment class 11: history, apparatus, procedure, observation

Line Spectrum of Hydrogen

The line spectrum of hydrogen refers to the unique pattern of colored lines produced when light passes through hydrogen gas or when hydrogen gas is excited, emitting light. This phenomenon played a crucial role in the development of quantum mechanics and was instrumental in understanding the behavior of atoms and their energy levels.

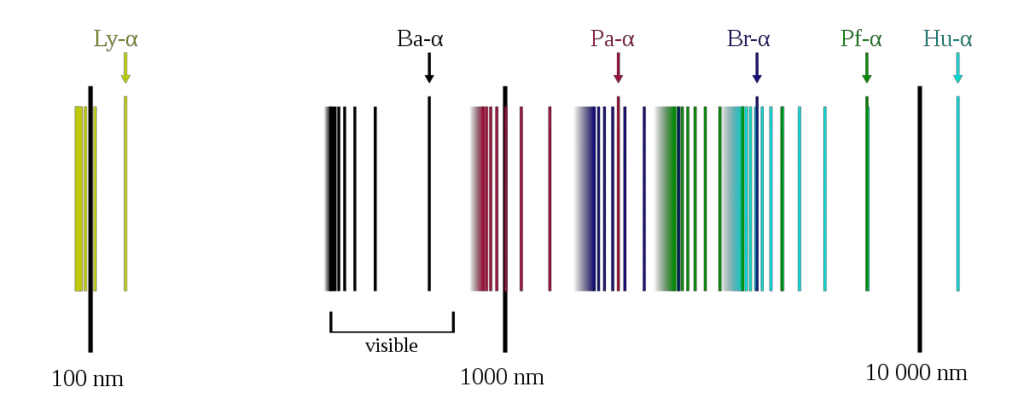
Observation

When scientists observed the light emitted by hydrogen gas under specific conditions, they noticed that the light wasn’t a continuous range of colors like a rainbow. Instead, they observed only distinct colored lines, separated by dark spaces.

Explanation

The line spectrum of hydrogen is a result of the behavior of electrons within hydrogen atoms. Hydrogen atoms consist of a single proton in the nucleus and one electron orbiting around it. When energy is supplied to hydrogen gas (e.g., by passing an electric current through it or heating it), some of the electrons in the atoms become excited and jump to higher energy levels or orbits.

Emission of Light

As these excited electrons return to their lower energy levels, they release the excess energy in the form of photons (light). Each electron releases a photon with a specific amount of energy corresponding to the energy difference between the higher and lower energy levels.

Distinct Energy Levels

In hydrogen, the energy levels that electrons can occupy are quantized, meaning they can only exist in certain discrete energy states. These energy levels are represented by whole numbers, with the lowest energy level called the ground state (n=1) and higher energy levels labeled as n=2, n=3, and so on.

Spectral Lines

Each colored line in the hydrogen line spectrum corresponds to the transition of an electron from a higher energy level (e.g., n=2, n=3) to a lower energy level (n=1). Each line is associated with a specific wavelength (or color) of light, and these wavelengths are determined by the energy differences between the energy levels involved in the electron transitions.

Significance

The line spectrum of hydrogen was a major puzzle for classical physics because it couldn’t be explained using traditional wave theories. It was only when scientists like Niels Bohr applied quantum theory that they successfully explained the hydrogen line spectrum and the quantized nature of energy levels in atoms. This work eventually led to the development of quantum mechanics, a fundamental theory describing the behavior of matter and energy at the atomic and subatomic scales. The hydrogen line spectrum remains one of the most iconic examples of quantum phenomena and continues to be studied extensively in modern physics.

Solved examples

1. Calculate (a) wavenumber and (b) frequency of yellow radiation having wavelength 5800 Å. Solution: (a) Calculation of wavenumber $(\bar{v})$ $$ \begin{aligned} \lambda=5800Å & =5800 \times 10^{-8} \mathrm{~cm} \\ & =5800 \times 10^{-10} \mathrm{~m} \end{aligned} $$ $$ \begin{aligned} \bar{v}=\frac{1}{\lambda} & =\frac{1}{5800 \times 10^{-10} \mathrm{~m}} \\ & =1.724 \times 10^6 \mathrm{~m}^{-1} \\ & =1.724 \times 10^4 \mathrm{~cm}^{-1} \end{aligned} $$ (b) Calculation of the frequency $(v)$ $$ \bar{v}=\frac{\mathrm{c}}{\lambda}=\frac{3 \times 10^8 \mathrm{~m} \mathrm{~s}^{-1}}{5800 \times 10^{-10} \mathrm{~m}}=5.172 \times 10^{14} \mathrm{~s}^{-1} $$

2. The Vividh Bharati station of All India Radio, Delhi, broadcasts on a frequency of $1,368 \mathrm{kHz}$ (kilohertz). Calculate the wavelength of the electromagnetic radiation emitted by the transmitter. Which part of the electromagnetic spectrum does it belong to? Solution: The wavelength, $\lambda$, is equal to $\mathrm{c} / v$, where $\mathrm{c}$ is the speed of electromagnetic radiation in a vacuum and $v$ is the frequency. Substituting the given values, we have $$ \begin{aligned} & \lambda=\frac{c}{v} \\ & =\frac{3.00 \times 10^8 \mathrm{~m} \mathrm{~s}^{-1}}{1368 \mathrm{kHz}} \\ & =\frac{3.00 \times 10^8 \mathrm{~m} \mathrm{~s}^{-1}}{1368 \times 10^3 \mathrm{~s}^{-1}} \\ & =219.3 \mathrm{~m} \end{aligned} $$ This is a characteristic radio wave wavelength.

3. Calculate the energy of one mole of photons of radiation whose frequency is $5 \times 10^{14}$ $\mathrm{Hz}$. Solution: Energy $(E)$ of one photon is given by the expression $$ \begin{aligned} & E=h v \\ & h=6.626 \times 10^{-34} \mathrm{~J} \mathrm{~s} \\ & V=5 \times 10^{14} \mathrm{~s}^{-1} \text { (given) } \\ & E=\left(6.626 \times 10^{-34} \mathrm{~J} \mathrm{~s}\right) \times\left(5 \times 10^{14} \mathrm{~s}^{-1}\right) \\ & =3.313 \times 10^{-19} \mathrm{~J} \end{aligned} $$ Energy of one mole of photons $$ \begin{aligned} & =\left(3.313 \times 10^{-19} \mathrm{~J}\right) \times\left(6.022 \times 10^{23} \mathrm{~mol}^{-1}\right) \\ & =199.51 \mathrm{~kJ} \mathrm{~mol} \end{aligned} $$

4. A 100-watt bulb emits monochromatic light of wavelength $400 \mathrm{~nm}$. Calculate the number of photons emitted per second by the bulb. Solution: $$ \begin{aligned} \text { Power of the bulb } & =100 \mathrm{watt} \\ & =100 \mathrm{~J} \mathrm{~s}^{-1} \end{aligned} $$ Energy of one photon $E=h v=h \mathrm{c} / \lambda$ $$ \begin{aligned} & =\frac{6.626 \times 10^{-34} \mathrm{~J} \mathrm{~s} \times 3 \times 10^8 \mathrm{~m} \mathrm{~s}^{-1}}{400 \times 10^{-9} \mathrm{~m}} \\ & =4.969 \times 10^{-19} \mathrm{~J} \end{aligned} $$ Number of photons emitted $$ \frac{100 \mathrm{~J} \mathrm{~s}^{-1}}{4.969 \times 10^{-19} \mathrm{~J}}=2.012 \times 10^{20} \mathrm{~s}^{-1} $$

5. The threshold frequency $v_0$ for a metal is $7.0 \times 10^{14} \mathrm{~s}^{-1}$. Calculate the kinetic energy of an electron emitted when radiation of frequency $v=1.0 \times 10^{15} \mathrm{~s}^{-1}$ hits the metal. Solution: According to Einstein’s equation $$ \begin{aligned} & \text { Kinetic energy }=1 / 2 m_{\mathrm{e}} v^2=h\left(v-v_0\right) \\ & =\left(6.626 \times 10^{-34} \mathrm{~J} \mathrm{~s}\right)\left(1.0 \times 10^{15} \mathrm{~s}^{-1}-7.0\times 10^{14} \mathrm{~s}^{-1}\right) \\ & =\left(6.626 \times 10^{-34} \mathrm{~J} \mathrm{~s}\right)\left(10.0 \times 10^{14} \mathrm{~s}^{-1}-7.0\times 10^{14} \mathrm{~s}^{-1}\right) \\ & =\left(6.626 \times 10^{-34} \mathrm{~J} \mathrm{~s}\right) \times\left(3.0 \times 10^{14} \mathrm{~s}^{-1}\right) \\ & =1.988 \times 10^{-19} \mathrm{~J} \\ & \end{aligned} $$

Stay tuned with Laws Of Nature for more useful and interesting content.