The Rayleigh-Jeans Law, also known as the Rayleigh-Jeans Formula or Rayleigh-Jeans Radiation Law, is a mathematical expression that describes the spectral distribution of energy radiated by blackbody radiation at thermal equilibrium.
It was formulated independently by Lord Rayleigh (John William Strutt) and Sir James Jeans in the late 19th century. However, it is important to note that the Rayleigh-Jeans Law is only valid at relatively low temperatures and long wavelengths and is superseded by the Planck radiation law for higher temperatures and shorter wavelengths.
The Rayleigh-Jeans Law provides an approximation of the spectral radiance (intensity per unit wavelength) of blackbody radiation as a function of temperature (T) and wavelength (λ).
In this short article, we will discuss Raleigh-Jeans Law in detail, so let’s get started…
Rayleigh-Jeans Law statement
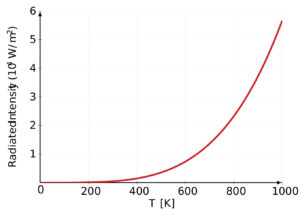
Rayleigh-Jeans law states that the spectral radiance (or energy density) of black body radiation is directly proportional to the temperature, and is inversely proportional to the fourth power of the wavelength.
Mathematically, the Rayleigh-Jeans law is expressed as:
$$B_{\lambda}(T) = \frac{2ck_B T}{\lambda^4}$$
Where:
- Bλ(T) is the spectral radiance (energy density) at wavelength λ and temperature T.
- c is the speed of light.
- kB is the Boltzmann constant.
- T is the temperature in Kelvin.
- λ is the wavelength of the radiation.
In terms of frequency, Rayleigh-Jeans Law is given as:
$$B_{\nu}(T) = \frac{2{\nu}^2k_B T}{c^2}$$
Derivation of Rayleigh-Jeans Law
To derive the Rayleigh-Jeans Law from scratch, we’ll start with some basic principles of classical physics and statistical mechanics. We’ll consider a cavity with blackbody radiation in thermal equilibrium at temperature T. We want to find the spectral radiance $(B_{\lambda}(T))$ at a given wavelength $(\lambda)$.
- Energy Density per Unit Wavelength (Classical Physics): First, we consider the energy density per unit wavelength, $(u_\lambda)$, which is the energy contained in a certain wavelength range per unit volume. This can be expressed as:
$$u_\lambda = \frac{E}{V \Delta\lambda}$$
Where:
- $(u_\lambda)$ is the energy density per unit wavelength.
- (E) is the total energy inside the cavity.
- (V) is the volume of the cavity.
- $(\Delta\lambda)$ is the wavelength interval.
- Counting States (Statistical Mechanics): In statistical mechanics, we consider the density of states in phase space. For electromagnetic waves, this means considering the number of different modes with wavelengths in the range $(\lambda)$ to $(\lambda + \Delta\lambda)$. The density of states $(g(\lambda))$ is proportional to $(\lambda^2)$ (this is a result of 3D space and is a geometric consideration).
$$g(\lambda) \propto \lambda^2$$
Maxwell-Boltzmann Distribution:
In statistical mechanics, the energy distribution of modes follows the Maxwell-Boltzmann distribution. The average energy of each mode can be calculated as:
$$E_{\lambda} = k_B T$$
Where:
- $(E_{\lambda})$ is the average energy of a mode.
- $(k_B)$ is the Boltzmann constant.
- (T) is the temperature.
- Total Energy Inside the Cavity: The total energy inside the cavity is the sum of the energies of all the modes. We integrate over all wavelengths to get this total energy: $$E = \int_0^\infty E_{\lambda} \cdot g(\lambda) \cdot \Delta\lambda$$
- Substituting the expressions for $(E_{\lambda})$ and $(g(\lambda))$ we derived earlier: $$E = \int_0^\infty k_B T \cdot (\text{constant}) \cdot \lambda^2 \cdot \Delta\lambda$$ $$E = k_B T \cdot \int_0^\infty \lambda^2 \cdot \Delta\lambda$$
- Energy Density per Unit Wavelength (Revisited): Now we can express the energy density per unit wavelength $(u_\lambda)$ using the total energy (E) we calculated:
$$u_\lambda = \frac{E}{V \Delta\lambda} = \frac{k_B T \cdot \int_0^\infty \lambda^2 \cdot \Delta\lambda}{V \Delta\lambda}$$
$$u_\lambda = \frac{k_B T}{V} \cdot \int_0^\infty \lambda^2 \, d\lambda$$
Now we have the expression for $(u_\lambda)$ in terms of temperature and volume.
Spectral Radiance $((B_{\lambda}(T)))$:
Spectral radiance $(B_{\lambda}(T))$ is defined as the power per unit area per unit solid angle per unit wavelength. We can relate $(u_\lambda)$ to $(B_{\lambda}(T))$ using the speed of light, (c), which relates power to energy:
$$B_{\lambda}(T) = \frac{c}{4} u_\lambda$$
$$B_{\lambda}(T) = \frac{c}{4} \cdot \frac{k_B T}{V} \cdot \int_0^\infty \lambda^2 \, d\lambda$$
$$B_{\lambda}(T) = \frac{2ck_B T}{\lambda^4}$$
This is the Rayleigh-Jeans Law for spectral radiance, derived from classical physics and statistical mechanics, and it describes the energy radiated per unit area, per unit solid angle, and unit wavelength at a given temperature (T).
Read Also:
- Rutherford atomic model: postulates, observations, and limitations, class 11
- Thomson model of atom: postulates, drawbacks, & significance, class 11
- Cathode Tube Ray Experiment class 11: working, procedure, observation, and conclusion
- Discovery of Electron class 11: chemistry, NCERT
- Discovery of proton class 11: chemistry NCERT
- Wave nature of electromagnetic radiation, class 11
Rayleigh-Jeans Law vs Planck Law
The Rayleigh-Jeans Law predicts that as temperature increases, spectral radiance also increases. However, it fails to accurately describe the behavior of blackbody radiation at high temperatures and short wavelengths.
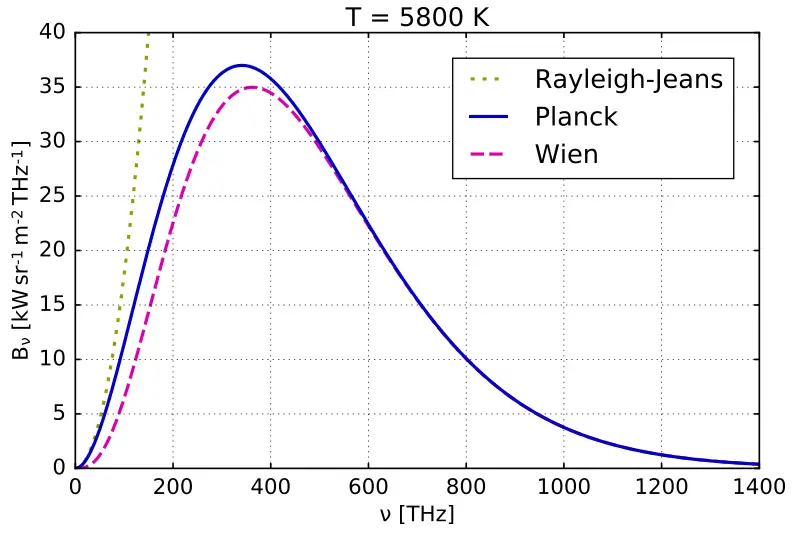
The Rayleigh-Jeans law accurately predicts experimental results when it comes to long wavelengths (low frequencies), but it significantly disagrees when it comes to short wavelengths (high frequencies). This inconsistency between observations and the predictions of classical physics is famously known as the ultraviolet catastrophe. Planck’s law, which provides the correct radiation for all frequencies, includes the Rayleigh-Jeans law as its low-frequency limit.
In the early 20th century, Max Planck developed a more accurate theory of blackbody radiation, known as Planck’s Law, which successfully explained the observed spectral distribution of energy and played a significant role in the development of quantum mechanics.
Planck’s Law, rather than the Rayleigh-Jeans Law, is used to describe blackbody radiation over a wide range of temperatures and wavelengths. Planck’s Law takes into account the quantization of energy levels and is consistent with experimental observations, making it a fundamental concept in modern physics and the foundation for quantum mechanics.
Rayleigh-Jeans Law comparison to Planck law
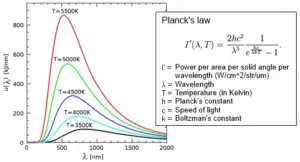
In 1900, Max Planck empirically obtained an expression for black-body radiation expressed in terms of wavelength $\lambda=c / v$ (Planck’s law):
$$
B_\lambda(T)=\frac{2 h c^2}{\lambda^5} \frac{1}{e^{\frac{h c}{\lambda k_{\mathrm{B}} T}}-1},
$$
where $h$ is the Planck constant, and $k_{\mathrm{B}}$ is the Boltzmann constant. Planck’s law does not suffer from an ultraviolet catastrophe and agrees well with the experimental data, but its full significance (which ultimately led to quantum theory) was only appreciated several years later. Since
$$
e^x=1+x+\frac{x^2}{2 !}+\frac{x^3}{3 !}+\cdots,
$$
then in the limit of high temperatures or long wavelengths, the term in the exponential becomes small, and the exponential is well approximated with the Taylor polynomial’s first-order term:
$$
e^{\frac{h c}{\lambda k_{\mathrm{B}} T}} \approx 1+\frac{h c}{\lambda k_{\mathrm{B}} T} .
$$
So
$$
\frac{1}{e^{\frac{h c}{\lambda k_{\mathrm{B}} T}}-1} \approx \frac{1}{\frac{h c}{\lambda k_{\mathrm{B}} T}}=\frac{\lambda k_{\mathrm{B}} T}{h c} .
$$
This results in Planck’s blackbody formula reducing to
$$
B_\lambda(T)=\frac{2 c k_{\mathrm{B}} T}{\lambda^4},
$$
which is identical to the classically derived Rayleigh-Jeans expression.
The same argument can be applied to the blackbody radiation expressed in terms of frequency $v=c / \lambda$. In the limit of small frequencies, that is $h \nu \ll k_{\mathrm{B}} T$
| $$ B_\nu(T)=\frac{2 h \nu^3}{c^2} \frac{1}{e^{\frac{h \nu}{k_{\mathrm{B}} T}}-1} \approx \frac{2 h \nu^3}{c^2} \cdot \frac{k_{\mathrm{B}} T}{h \nu}=\frac{2 \nu^2 k_{\mathrm{B}} T}{c^2} . $$ |
This last expression is the Rayleigh-Jeans law in the limit of small frequencies.
Read Also:
- Black body radiation class 11: A complete guide
- Planck’s Quantum Theory class 11: A Comprehensive Guide
- Particle nature of electromagnetic radiation, class 11
- Exploring the Bohr Atomic Model: A Comprehensive Guide
Limitations of Rayleigh-Jeans Law
The Rayleigh-Jeans Law, which describes the spectral radiance of blackbody radiation, was developed based on classical physics and statistical mechanics. While it provides a reasonable approximation for longer wavelengths, lower frequencies, and higher temperatures, it has limitations, especially at shorter wavelengths and lower temperatures. Some main limitations of the Rayleigh-Jeans Law are:
- Ultraviolet Catastrophe: The Rayleigh-Jeans Law predicts that the energy radiated by a blackbody diverges as the wavelength approaches zero, leading to an infinite energy density at short wavelengths. This issue is known as the “ultraviolet catastrophe” and was a significant problem in classical physics.
- Incompatibility with Quantum Mechanics: The Rayleigh-Jeans Law was developed before the advent of quantum mechanics. In reality, the quantization of energy levels for electromagnetic radiation, as described by Planck’s blackbody radiation formula and later quantum theory, plays a crucial role in accurately describing the behavior of blackbody radiation.
- Failure at Low Temperatures: At low temperatures, the Rayleigh-Jeans Law significantly underestimates the energy radiated by black bodies. It fails to describe the observed behavior of objects that radiate very little energy compared to what the law predicts at those temperatures.
- Inapplicability to Short Wavelengths: The Rayleigh-Jeans Law is not suitable for describing the behavior of blackbody radiation at short wavelengths (e.g., visible light, ultraviolet, and X-rays) because it overestimates the radiated energy.
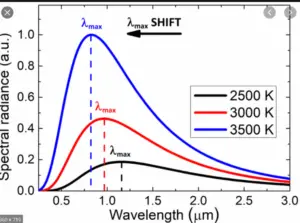
- Violates the Wien Displacement Law: The Rayleigh-Jeans Law does not follow the Wien Displacement Law, which states that the wavelength at which the spectral radiance is maximum is inversely proportional to the temperature of the blackbody. The Rayleigh-Jeans Law predicts a constant spectral radiance at all wavelengths, which is not observed experimentally.
- Lack of Predictive Accuracy: The Rayleigh-Jeans Law does not accurately predict the observed behavior of blackbody radiation across the entire electromagnetic spectrum. It was an empirical formula that worked well for some ranges of temperature and wavelength but failed in other cases.
Conclusion
In conclusion, the Rayleigh-Jeans law provides a classical description of the spectral radiance of black body radiation based on classical physics principles and assumptions. It predicts that the spectral radiance is directly proportional to the temperature and frequency of the radiation and inversely proportional to the square of the wavelength.
However, the Rayleigh-Jeans law fails to accurately predict the observed behavior of black body radiation at shorter wavelengths, known as the “ultraviolet catastrophe.” This discrepancy highlighted the limitations of classical physics in describing the behavior of electromagnetic waves and led to the development of quantum mechanics.
Despite its limitations, the Rayleigh-Jeans law played a significant role in the historical understanding of black body radiation and served as a stepping stone towards the formulation of more accurate theories, such as Planck’s law, which successfully explained the distribution of black body radiation across all wavelengths.
Stay tuned with Laws Of Nature for more useful and interesting content.
References: