In this short article, we will derive a relationship between focal length and radius of curvature. So, let’s get started…
Relation between focal length and radius of curvature
Relation between ƒ and R: Consider a ray parallel to the principal axis, incident at point B of a spherical mirror (concave or convex) of a small aperture. After reflection from the mirror, this ray converges to point F (in the case of a concave mirror) or appears to diverge from point F (in the case of a convex mirror), obeying the laws of reflection. Thus, F is the focus of the mirror, C is the centre of curvature, CP is the radius of curvature, and BC is a normal mirror at point B.
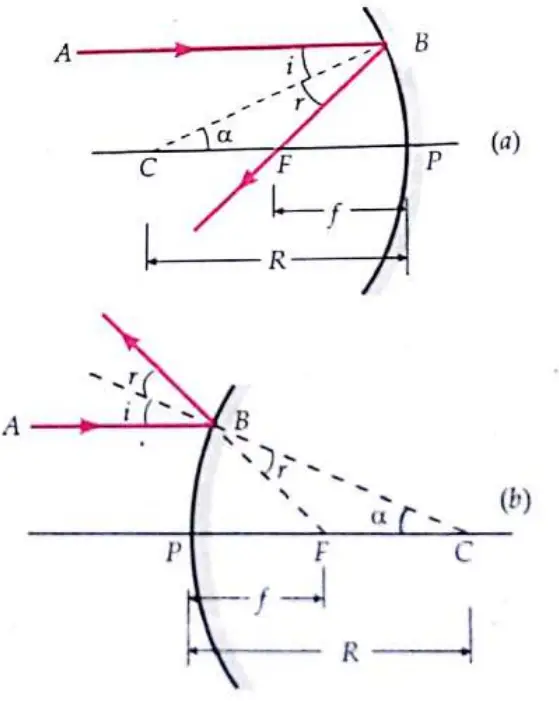
According to the law of reflection,
$$
\angle i=\angle r
$$
As $A B$ is parallel to $P C$,
$$
\begin{array}{ll}
\therefore \text { In } \triangle B F C, & \angle \alpha=\angle i \\
\text { Hence } & \angle r=\angle \alpha \\
\text { For a mirror of } & C F=F B
\end{array}
$$
For a mirror with a small aperture,
$$
F B \simeq F P \quad \therefore \quad C F \simeq F P
$$
Hence
$$
C P=C F+F P=F P+F P=2 F P
$$
or
$$
R=2 f \text { or } f=\frac{R}{2}
$$
or $$\text{Focal length}=\frac{1}{2} \times \text{Radius of curvature}$$
or $$ \text{Radius of curvature} = 2 \times \text{Focal length}$$
So, the relationship between focal length and radius of curvature is that the radius of curvature is two times the focal length.
Read More:
- Behaviour of light at the interface of two media
- Cartesian sign convention for spherical mirrors
- Optics: definition, types, and applications, class 12
- Simple microscope Class 12, Definition, Magnification, working, Parts And Uses
- Reflection of light class 12: definition and types
- Spherical mirrors: definition, types, and terminologies
Stay tuned with Laws Of Nature for more useful and interesting content.