Wien’s displacement law: statement, formula derivation, & examples

The Wien’s Displacement Law, formulated by the German physicist Wilhelm Wien in 1893, is a fundamental principle in the field of thermal radiation and blackbody radiation. This law describes the relationship between the temperature of an ideal blackbody (a theoretical object that absorbs all incident radiation and emits radiation at all wavelengths) and the wavelength at which it emits the maximum amount of radiation.

In this article, we will discuss Wien’s displacement law, its statement, and will derive its formula, so let’s begin.

Wien’s displacement law: statement

Wien’s Displacement Law states that the wavelength at which the emission of radiation from a blackbody spectrum is maximized is inversely proportional to the absolute temperature of the blackbody. Mathematically, it can be expressed as:

$$\lambda_{\text{max}} = \frac{b}{T}$$

Where:

• $\lambda_{\text{max}}$ is the wavelength at which the blackbody emits the most radiation (peak wavelength).
• T is the absolute temperature of the blackbody in Kelvin.
• The constant in the equation is known as Wien’s displacement constant, denoted by the symbol “b.”

Wien’s displacement constant, “b,” is approximately equal to $2.898 \times 10^{-3}$ meters per Kelvin $(m·K^{-1})$.

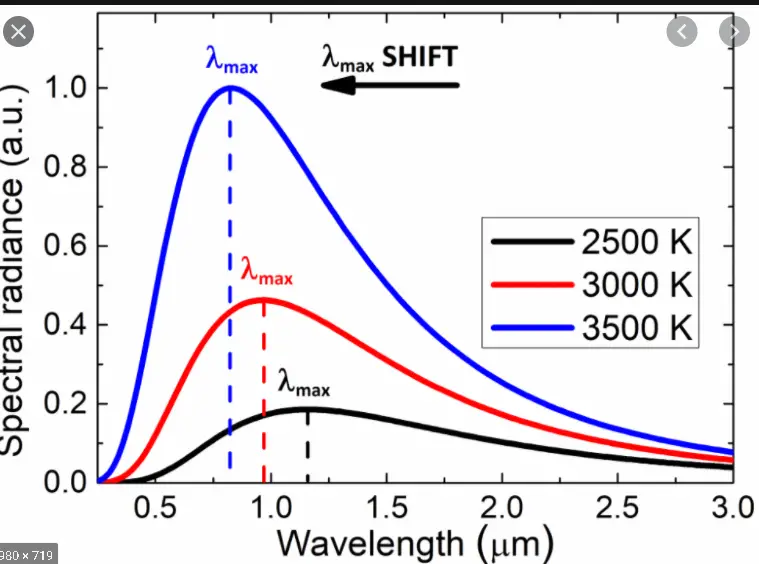
In simple terms, this law tells us that as the temperature of a blackbody increases, the peak of its radiation spectrum shifts toward shorter wavelengths (e.g., from red to blue). Conversely, as the temperature decreases, the peak shifts toward longer wavelengths (e.g., from blue to red). This relationship is fundamental to understanding how the color or dominant wavelength of thermal radiation emitted by objects changes with temperature.

Key points to note about the Wien Displacement Law

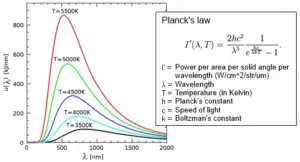
1. As the temperature of a blackbody increases, the wavelength at which it emits the most radiation $\lambda_{\text{max}}$ becomes shorter (shifts toward the blue end of the electromagnetic spectrum).
2. Conversely, as the temperature decreases, the peak wavelength becomes longer (shifting toward the red end of the spectrum).
3. This law is consistent with our everyday observations. For example, objects like stars with very high temperatures appear bluish because they emit most of their radiation at shorter wavelengths (e.g., in the visible and ultraviolet parts of the spectrum). Cooler objects, like red-hot metal or the Earth’s surface, emit most of their radiation at longer wavelengths, making them appear reddish or even infrared to our eyes.
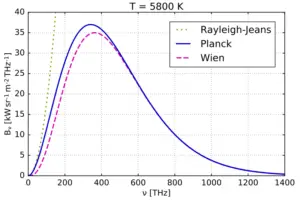
4. The Wien Displacement Law is a direct consequence of the Planck radiation law, which describes the spectral distribution of radiation emitted by a blackbody at different wavelengths at a given temperature.

Wien’s displacement law formula derivation

To derive Wien’s Displacement Law formula, we can start with the Planck radiation law, which describes the spectral distribution of radiation emitted by a blackbody at a given wavelength and temperature. The formula for Planck’s radiation law is given by:

$$
u_\lambda(\lambda, T)=\frac{2 h c^2}{\lambda^5} \frac{1}{e^{h c / \lambda k T}-1} .
$$
Differentiating $u(\lambda, T)$ with respect to $\lambda$ and setting the derivative equal to zero gives:

which can be simplified to give:
$$
\frac{h c}{\lambda k T} \frac{e^{h c / \lambda k T}}{e^{h c / \lambda k T}-1}-5=0 .
$$
By defining:
$$
x \equiv \frac{h c}{\lambda k T}
$$
the equation becomes one in the single variable $x$ :
$$
\frac{x e^x}{e^x-1}-5=0 .
$$
which is equivalent to:
$$
x=5\left(1-e^{-x}\right) .
$$
This equation is solved by
$$
x=5+W_0\left(-5 e^{-5}\right)
$$
where $W_0$ is the principal branch of the Lambert $W$ function, and gives $x=4.965114231744276303 \ldots . .$ Solving for the wavelength $\lambda$ in millimeters, and using kelvins for the temperature yields:

Read Also:

• Rutherford atomic model: postulates, observations, and limitations, class 11
• Thomson model of atom: postulates, drawbacks, & significance, class 11
• Cathode Tube Ray Experiment class 11: working, procedure, observation, and conclusion
• Discovery of Electron class 11: chemistry, NCERT
• Discovery of proton class 11: chemistry NCERT
• Wave nature of electromagnetic radiation, class 11

Examples of Wien’s displacement law

Wien’s Displacement Law is a fundamental principle that helps explain various real-life phenomena related to the emission of electromagnetic radiation by objects of different temperatures. Here are some real-life examples where Wien’s Displacement Law can be observed:

1. Incandescent Light Bulbs: When an incandescent light bulb is turned on, it heats up and begins to emit visible light. As it gets hotter, the color of the emitted light changes from reddish to white and then to bluish-white. This change in color temperature corresponds to the shifting of the peak wavelength of the emitted light, as predicted by Wien’s Displacement Law.
2. Stellar Colors: The color of stars in the night sky depends on their surface temperatures. Hotter stars, like blue giants, appear bluish-white, while cooler stars, like red giants, appear reddish. This variation in color is due to the different peak wavelengths of radiation emitted by stars, as described by Wien’s Displacement Law.
3. Thermal Imaging: In thermal imaging cameras, Wien’s Displacement Law is used to determine the temperature of objects based on the infrared radiation they emit. Hotter objects emit shorter-wavelength infrared radiation, which corresponds to higher temperatures, while cooler objects emit longer-wavelength infrared radiation, indicating lower temperatures.
4. Astrophysics: Wien’s Displacement Law is crucial for determining the temperatures of celestial bodies, such as stars and galaxies, by analyzing their spectral emissions. By examining the peak wavelengths in their spectra, astronomers can estimate the temperatures of these objects.
5. Climate Science: Wien’s Displacement Law is also relevant in climate science. The earth’s surface emits thermal radiation, and its temperature affects the wavelength distribution of this radiation. This understanding is essential for modeling Earth’s energy balance and predicting the effects of climate change.
6. Cooking: When heating a metal object, such as a piece of iron or steel, in a fire or on a stovetop, the color of the metal changes as it gets hotter. Initially, it may appear red, then turn orange, yellow, and eventually white as it gets hotter. This color change follows the predictions of Wien’s Displacement Law.
7. Candle Flames: The color of a candle flame depends on the temperature of the burning gases. The inner part of a candle flame, where combustion is most complete and temperatures are higher, appears bluish-white, while the outer, cooler part appears yellow or orange, demonstrating the temperature-dependent color changes consistent with Wien’s Displacement Law.

Frequently Asked Questions (FAQs)