Stefan-Boltzmann law: statement, constant & formula derivation

The Stefan-Boltzmann Law, also known as Stefan’s law, is a fundamental law in physics that describes how the intensity of thermal radiation emitted by a matter is related to its temperature. This law is named after two pioneering scientists: Josef Stefan, who empirically established the relationship, and Ludwig Boltzmann, who provided a theoretical derivation.

In this article, we will discuss the basics of the Stefan-Boltzmann law and its statement, and we will derive the formula for it. So, let’s begin…

What is the Stefan-Boltzmann law?

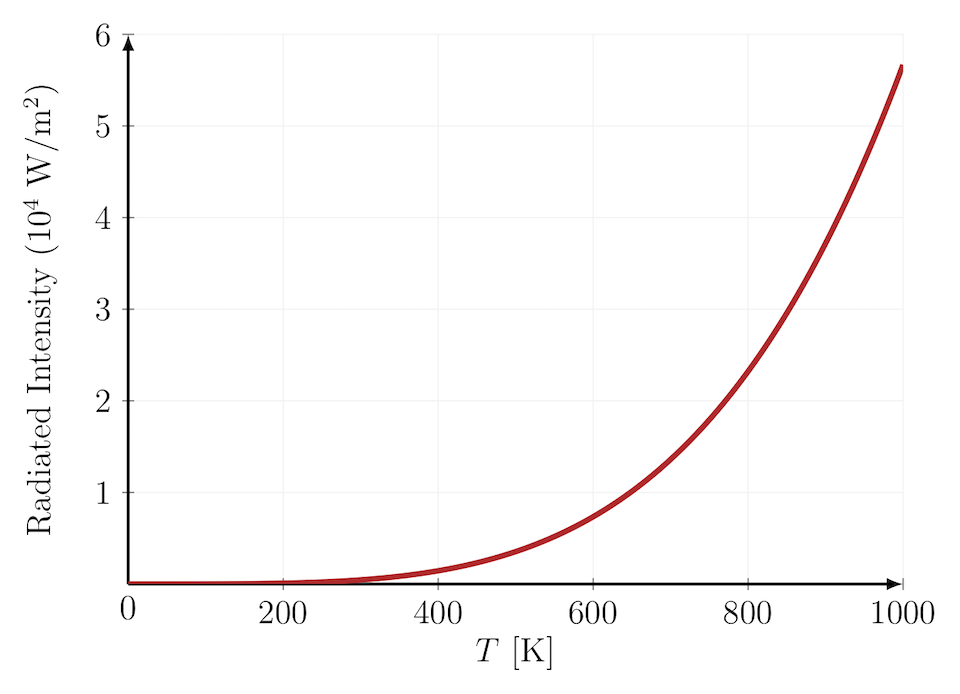
Stefan-Boltzmann law is a fundamental law in physics that relates a black body’s total amount of energy radiated per unit surface area to its temperature. The law states that the power radiated (P) by a black body is directly proportional to the fourth power of its absolute temperature (T).

Stefan-Boltzmann law: statement

The Stefan-Boltzmann law states that the total energy radiated per unit surface area per unit time (also known as radiant exitance) by an ideal absorber or emitter, such as a black body, is directly proportional to the fourth power of the black body’s temperature, ‘T’. This law is mathematically expressed as:

$$E = \sigma T^4$$

Where:

• (E) represents the radiant exitance (energy emitted per unit area per unit time).
• $(\sigma)$ is the Stefan-Boltzmann constant, a fundamental physical constant that has a specific numerical value approximately equal to $\sigma \approx 5.67 \times 10^{-8} \, \text{W m}^{-2} \text{K}^{-4} $
• (T) is the absolute temperature of the black body in Kelvin.

In the general case:

In the general case, the formula for the Stefan-Boltzmann law that includes emissivity ($\varepsilon$) is as follows:

$$E = \varepsilon \sigma T^4$$

In this formula:

• (E) represents the radiant exitance, the total energy radiated per unit surface area per unit time (in watts per square meter, W/m²).
• $(\varepsilon)$ is the emissivity of the object, which is a dimensionless coefficient that describes how effectively the object emits radiation compared to an ideal black body (where (\varepsilon = 1) for a perfect black body and ($\varepsilon$
• $(\sigma)$ is the Stefan–Boltzmann constant with a value of approximately $5.67 \times 10^{-8}$ W/(m²·K⁴).
• (T) is the absolute temperature of the object in Kelvin.

This formula takes into account the emissivity of the object, which indicates how efficiently it emits radiation compared to an ideal black body. For a perfect black body, $(\varepsilon)$ equals 1, but for real objects, it can be less than 1 to account for the differences in radiative efficiency.

Stefan-Boltzmann constant

The Stefan-Boltzmann constant, denoted as (\sigma), is a fundamental constant in physics that appears in the Stefan-Boltzmann law. It relates the total radiant energy emitted per unit surface area by a blackbody to its absolute temperature. The formula for the Stefan-Boltzmann constant is:

$$
\sigma = \frac{2\pi^5k^4}{15h^3c^2}
$$

Where:

• $(\sigma)$ (sigma) is the Stefan-Boltzmann constant.
• $(\pi)$ (pi) is the mathematical constant pi, approximately equal to 3.14159.
• (k) is the Boltzmann constant, approximately equal to $(1.380649 \times 10^{-23}) J/K$ (joules per kelvin).
• (h) is the Planck constant, approximately equal to $(6.62607015 \times 10^{-34}) J·s$ (joule-seconds).
• (c) is the speed of light in a vacuum, approximately equal to 299,792,458 meters per second.

As of the 2019 redefinition of SI base units, which establishes exact fixed values for $k, h$, and $c$, the Stefan-Boltzmann constant is exactly:

Thus,
$$
\sigma=5.670374419 \ldots \times 10^{-8} \mathrm{~W} \mathrm{~m}^{-2} \mathrm{~K}^{-4} .
$$
Prior to this, the value of $\sigma$ was calculated from the measured value of the gas constant.

$$ \sigma=\left[\frac{2 \pi^5\left(1.380649 \times 10^{-23}\right)^4}{15\left(2.99792458 \times 10^8\right)^2\left(6.62607015 \times 10^{-34}\right)^3}\right] \frac{\mathrm{W}}{\mathrm{m}^2 \cdot \mathrm{K}^4} $$

Now, let’s create a table showing the value of the Stefan-Boltzmann constant in different systems of units:

System of Units	Value of Stefan-Boltzmann Constant ($\sigma$)
SI (International System of Units)	$(5.67 \times 10^{-8})$ W/(m²·K⁴)
CGS (Centimeter-Gram-Second)	$(5.67 \times 10^{-5})$ erg/(cm²·s·K⁴)
Imperial (British Thermal Units)	$(1.71 \times 10^{-9})$ BTU/(hr·ft²·°R⁴)
Thermochemisrty	$1.170937\times10^{-7}$cal⋅cm−2⋅day−1⋅K−4

These are the most commonly used units for the Stefan-Boltzmann constant in various systems. In SI units, it is measured in watts per square meter per kelvin to match the units of the Stefan-Boltzmann law. In the CGS system, it is measured in ergs per square centimeter per second per kelvin, and in the Imperial system, it is measured in British Thermal Units (BTU) per hour per square foot per degree Rankine to match the respective unit systems.

Derivation of Stefan Boltzmann Law formula

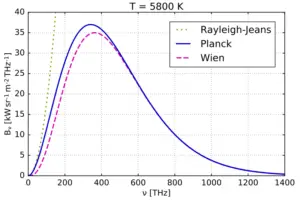
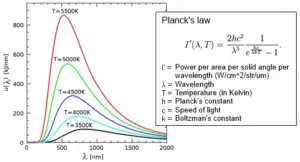
The Stefan-Boltzmann law formula can be derived from Planck’s law by integrating Planck’s law over all wavelengths and considering the total power radiated by a black body. Here’s a step-by-step derivation:

Step 1: Start with Planck’s law:
$$
B(\lambda, T) = \frac{{2hc^2}}{{\lambda^5}} \cdot \frac{1}{{e^{\frac{{hc}}{{\lambda k T}}} – 1}}
$$
where:

• (B(\lambda, T)) is the spectral radiance (power per unit area per unit wavelength) at a given wavelength (\lambda) and temperature (T).
• (h) is Planck’s constant.
• (c) is the speed of light, and
• (k) is Boltzmann’s constant.

Step 2: The total power radiated by a black body is obtained by integrating the spectral radiance over all wavelengths. Let’s denote it as (P(T)):
$$
P(T) = \int_{0}^{\infty} B(\lambda, T) \cdot \pi \cdot R^2 \cdot d\lambda
$$
where:

• (R) is the radius of the black body.
• $(d\lambda)$ represents a small change in wavelength, and
• $(\pi \cdot R^2)$ is the surface area of the black body.

Step 3: Simplify the integral by substituting variables. Let $(x = \frac{{hc}}{{\lambda k T}})$. Notice that $(\frac{{dx}}{{d\lambda}} = -\frac{{hc}}{{\lambda^2 k T}})$. Rearrange the variables to solve for $(d\lambda)$:
$$
d\lambda = -\frac{{\lambda^2 k T}}{{hc}} \cdot dx
$$
Substituting this back into the integral, we get:

$$P(T) = \pi \cdot R^2 \int_{0}^{\infty} \frac{{2hc^2}}{{\lambda^5}} \cdot \frac{1}{{e^x – 1}} \cdot \left(-\frac{{\lambda^2 k T}}{{hc}} \cdot dx\right)$$

Step 4: Simplify the constants in the integral:
$$
P(T) = -\frac{{2\pi k^4 R^2}}{{c^2h^3}} T^4 \int_{0}^{\infty} \frac{{x^3}}{{e^x – 1}} dx
$$

Step 5: The integral on the right is standard and goes by many names: it is a particular case of a Bose–Einstein integral, the polylogarithm, or the Riemann zeta function. The value of the integral is $\Gamma (4)\zeta (4) =\frac{\pi^4}{15}$ (where $\Gamma(s)$ is the Gamma function), giving the result that, for a perfect blackbody surface:
$$
\Gamma (4)\zeta (4) = \int_{0}^{\infty} \frac{{x^3}}{{e^x – 1}} dx = \frac{{\pi^4}}{{15}}
$$

Step 6: Substitute the value of the integral back into the equation.
$$
P(T) = -\frac{{2\pi k^4 R^2}}{{c^2h^3}} T^4 \cdot(\Gamma (4)\zeta (4))
$$
Simplifying further gives:
$$
P(T) = \frac{{2\pi^5 k^4 R^2}}{{15c^2h^3}} T^4
$$

Step 7: Recognize that $\displaystyle\left(\frac{{2\pi^5 k^4}}{{15c^2h^3}}\right)$ is a constant, denoted as $(\sigma)$, known as the Stefan-Boltzmann constant:
$$
\sigma = \frac{{2\pi^5k^4}}{{15c^2h^3}}
$$

Step 8: Therefore, the final form of the Stefan-Boltzmann law is obtained:
$$
P(T) = \sigma \cdot T^4
$$

And that’s the derived Stefan-Boltzmann law from Planck’s law!

Read Also:

• Rutherford atomic model: postulates, observations, and limitations, class 11
• Thomson model of atom: postulates, drawbacks, & significance, class 11
• Cathode Tube Ray Experiment class 11: working, procedure, observation, and conclusion
• Discovery of Electron class 11: chemistry, NCERT
• Discovery of proton class 11: chemistry NCERT
• Wave nature of electromagnetic radiation, class 11
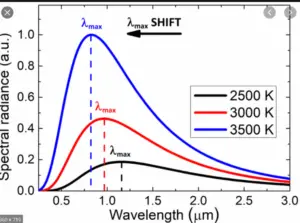
• Wien’s displacement law: statement, formula derivation, & examples

Applications of Stefan-Boltzmann law

The Stefan-Boltzmann law has various important applications in physics, astronomy, engineering, and other fields due to its role in describing how the radiant energy emitted by an object is related to its temperature. Here are some key applications:

Astronomy:

• Stellar Luminosity: Astronomers use the Stefan-Boltzmann law to estimate the luminosity (total energy output) of stars by measuring the flux of radiation received on Earth and knowing the star’s distance. This is essential for classifying and understanding stars.

Climate Science:

• Earth’s Energy Balance: The Stefan-Boltzmann law is used to study the Earth’s energy balance, particularly in climate science. It helps model the radiative heat exchange between the Earth’s surface, atmosphere, and outer space, influencing climate models.

Engineering and Thermodynamics:

• Heat Transfer: Engineers and scientists use the law to analyze and design systems involving heat transfer. It’s crucial to understand how various objects, such as engines or electronic devices, dissipate heat.

Material Science:

• Infrared Thermography: Infrared cameras use the Stefan-Boltzmann law to convert the thermal radiation emitted by objects into temperature measurements. This is valuable for detecting defects in materials, monitoring industrial processes, and conducting research.

Space Exploration:

• Spacecraft Thermal Design: Engineers apply the law to design thermal protection systems for spacecraft. It helps calculate the amount of heat radiated away from spacecraft and ensures they can withstand extreme temperature variations in space.

Medical Imaging:

• Medical Thermography: Infrared imaging in medical applications relies on the Stefan-Boltzmann law to convert thermal radiation from the human body into temperature maps. This is used for diagnosing conditions and monitoring patient health.

Energy Efficiency:

• Energy-Efficient Building Design: Architects and engineers use the law to optimize the design of energy-efficient buildings. Understanding how heat is radiated and absorbed by building materials helps reduce energy consumption.

Environmental Monitoring:

• Environmental Remote Sensing: The law is applied in remote sensing techniques, such as measuring the temperature of Earth’s surfaces from satellites. This data is used for environmental monitoring, agriculture, and land-use planning.

Laboratory Research:

• Material Properties: Scientists use the Stefan-Boltzmann law in laboratory experiments to study the thermal properties of materials, including emissivity (the efficiency of an object to emit thermal radiation).

Nuclear Reactors:

• Nuclear Reactor Design: In the design and safety analysis of nuclear reactors, understanding the heat generation and removal processes is critical. The Stefan-Boltzmann law is used to calculate heat transfer rates.

These applications highlight the wide-ranging significance of the Stefan-Boltzmann law in various scientific, technological, and industrial fields, where the law’s relationship between temperature and radiative energy is fundamental for analysis and design.

Frequently Asked Questions (FAQs)