Black Body Radiation Class 11: A Complete Guide

Inside Story

Introduction

Black body radiation is the electromagnetic radiation emitted by an idealized object called a black body. A black body is an object that absorbs all radiation and doesn’t reflect or transmit any of it. Consequently, it appears completely black when its temperature is consistent. Black body radiation is a fundamental idea in physics and is essential for understanding numerous phenomena, such as star behavior, the generation of thermal radiation, and the advancement of quantum mechanics.

In this article, we will discuss the concept of black-body radiation, its definition, characteristics, supporting laws, applications, and how it give rise to quantum mechanics in detail. So let’s get started…

What is a black body?

Black body definition: A black body is an idealized object in physics that absorbs all incident electromagnetic radiation, regardless of wavelength or frequency, without reflecting or transmitting any of it. When a black body is in thermal equilibrium with its surroundings, it emits radiation, known as black body radiation, in a characteristic manner.

In theory, a black body is a perfect absorber and emitter of radiation. It absorbs all radiation that falls upon it, converting it into internal energy. Simultaneously, it emits radiation across a broad range of wavelengths. The distribution of this radiation depends solely on the temperature of the black body and follows a specific pattern known as the Planck radiation law.

Black body radiation: definition, equation, formula, class 11 — Black-body radiation, source: Chemistry LibreTexts

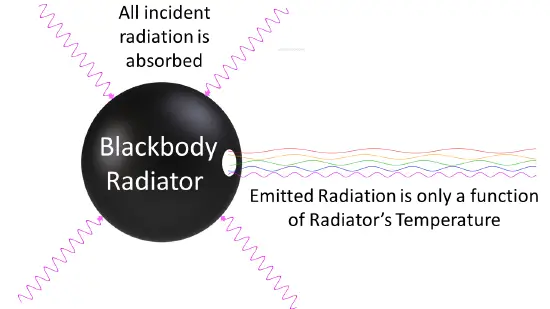
The concept of a black body is often used as a theoretical construct to analyze and understand the behavior of real objects that approximate their properties. While true black bodies do not exist in nature, some objects, such as a small hole in a cavity or a hollow sphere, can closely approximate the behavior of a black body over specific ranges of wavelengths and under certain conditions.

Read Also

Characteristics of black body radiation

Black body radiation exhibits several distinctive characteristics. Here are some important characteristics of black body radiation:

Continuous Spectrum: Black body radiation emits radiation over a continuous range of wavelengths, covering the entire electromagnetic spectrum. This means it produces radiation at all frequencies, from radio waves to gamma rays.
Temperature Dependence: The intensity and distribution of black body radiation depend solely on the temperature of the black body. As the temperature increases, the intensity of the radiation increases, and the peak wavelength shifts to shorter wavelengths. This relationship is described by Planck’s law.
Thermal Equilibrium: Black body radiation is emitted when a black body is in thermal equilibrium with its surroundings. In this state, the rate of energy absorbed by the black body from incident radiation is equal to the rate of energy it emits.
Absorption and Emission: A black body absorbs all incident radiation that falls upon it, with none of it being reflected or transmitted. It then re-emits this energy as black body radiation. The absorption and emission processes are balanced at thermal equilibrium.
Universality: Black body radiation is considered universal because its properties are independent of the material or composition of the object. The radiation emitted by a black body is solely determined by its temperature, making it a fundamental concept in physics.
Planck Distribution: The spectral distribution of black body radiation follows a specific pattern described by Planck’s law. The law states that the intensity of radiation at different wavelengths is determined by the temperature of the black body, with the peak intensity occurring at a specific wavelength related to the temperature.

Energy Quantization: The study of black body radiation played a crucial role in the development of quantum mechanics. Max Planck introduced the concept of quantized energy levels to explain the observed properties of black body radiation. This breakthrough paved the way for significant advancements in our understanding of the microscopic world, enabling us to gain deeper insight into the workings of the universe.

Idealized vs. real-world black bodies

When discussing black bodies, it is important to distinguish between idealized black bodies and real-world black bodies. Here’s a comparison of their characteristics:

Idealized Black Bodies:

Perfect Absorption: Idealized black bodies are assumed to absorb all incident radiation that falls upon them, regardless of wavelength or frequency. They do not reflect or transmit radiation.
Perfect Emission: Idealized black bodies emit radiation across the entire electromagnetic spectrum in a continuous manner, following the Planck radiation law. The emitted radiation is solely determined by the temperature of the black body.
Universality: The properties of idealized black bodies are independent of their material composition. This means that all idealized black bodies at the same temperature would emit the same radiation spectrum.
Infinite Conductivity: Idealized black bodies are assumed to have infinite conductivity, meaning that they can instantly distribute any absorbed energy uniformly throughout their entire volume.

Real-World Black Bodies:

Imperfect Absorption: Real-world black bodies, such as objects in everyday life, do not perfectly absorb all incident radiation. They may reflect or transmit a portion of the incident radiation, resulting in a deviation from ideal black body behavior.
Deviations in Emission: Real-world black bodies may deviate from the idealized black body radiation spectrum due to various factors, such as impurities, surface roughness, and quantum mechanical effects. These deviations can lead to modifications in the emitted radiation spectrum.
Material Dependence: Real-world black bodies exhibit material dependence, meaning that different materials will have different absorption and emission characteristics. The properties of real black bodies are influenced by factors such as the material’s conductivity and optical properties.

Finite Conductivity: Real-world black bodies have finite conductivity, which means that they may have limitations in distributing absorbed energy uniformly throughout their volume. This can result in localized temperature variations and deviations from ideal black body behavior.

It is important to note that while real-world black bodies may not exhibit perfect behavior, scientists can approximate idealized black body behavior using specific objects or setups that come close to the theoretical concept. These approximations help in practical applications and scientific studies involving black body radiation.

Read Also

AC circuit containing resistor and inductor in series

The experimental observations in black body radiation

Experimental observations of black body radiation played an important role in the development of quantum mechanics and the understanding of this phenomenon. Here are some key experimental observations related to black body radiation:

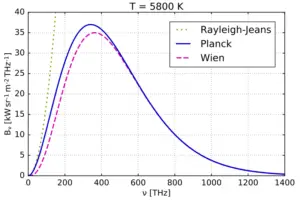
Planck’s Law: In 1900, Max Planck proposed a mathematical expression to describe the spectral distribution of black body radiation. His law successfully matched experimental data, known as Planck’s law or Planck’s radiation law. It accurately described the intensity of radiation emitted at different wavelengths by a black body at a given temperature.

Wien’s Displacement Law: In 1893, Wilhelm Wien discovered an empirical relationship between the wavelength at which the spectral intensity of black body radiation is maximum and the temperature of the black body. According to Wien’s displacement law, the product of the maximum wavelength $(λ_{max})$ and the temperature (T) of the black body is a constant known as Wien’s displacement constant (denoted by the symbol ‘b’).
Stefan-Boltzmann Law: The Stefan-Boltzmann law, derived from experimental measurements, establishes the relationship between the total power radiated by a black body and its temperature. This law states that the total power radiated per unit surface area is proportional to the fourth power of the absolute temperature of the black body. Experimental measurements confirmed the validity of this law.
Ultraviolet Catastrophe: Before the development of quantum mechanics, classical physics predicted an infinite amount of energy being emitted at high frequencies in black body radiation, known as the ultraviolet catastrophe. However, experimental observations showed that the intensity of radiation decreased at higher frequencies, contradicting classical predictions and leading to the development of quantum mechanics.

Black Body Radiation Spectra: Experimental measurements of black body radiation spectra confirmed the existence of a continuous distribution of wavelengths emitted by a black body at a given temperature. The shape of the spectra matched the predictions of Planck’s law and provided empirical evidence supporting the quantization of energy in the form of discrete energy packets, or quanta.

These experimental observations were important in the development of quantum mechanics and the understanding of the quantized nature of energy and the behavior of electromagnetic radiation. They highlighted the discrepancies between classical physics and the observed behavior of black body radiation, leading to the development of a new theoretical framework that became the foundation of modern physics.

The Planck Radiation Law

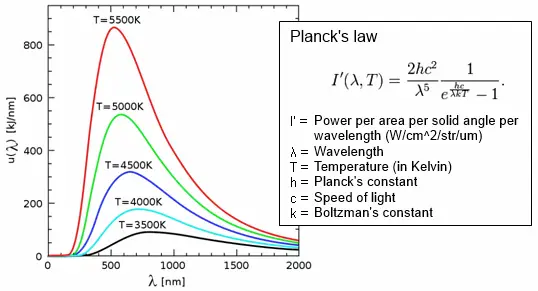
The Planck radiation law, also known as Planck’s law, describes the spectral distribution of electromagnetic radiation emitted by a black body in thermal equilibrium. It was formulated by the German physicist Max Planck in 1900 and played a pivotal role in the development of quantum mechanics.

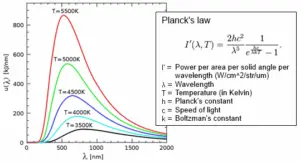
Planck radiation law statement: The Planck radiation law states that the spectral radiance, or the amount of radiation emitted per unit area, per unit solid angle, and per unit wavelength, by a black body at a given temperature, is proportional to the wavelength raised to the power of minus five, multiplied by the reciprocal of the exponential function of the ratio of the wavelength and the product of the temperature and a fundamental constant called Planck’s constant (h), and the speed of light (c).

Mathematically, Planck’s law is expressed as:

$$B(\lambda, T) = \frac{2hc^2}{\lambda^5} \cdot \frac{1}{e^{\frac{hc}{\lambda kT}} – 1}$$

where:
B(λ, T) is the spectral radiance of the black body at a given wavelength λ and temperature T,
h is Planck’s constant (approximately 6.626 x 10^-34 Joule-seconds),
c is the speed of light (approximately 3 x 10^8 meters per second),
k is the Boltzmann constant (approximately 1.38 x 10^-23 Joules per Kelvin),
λ is the wavelength of the emitted radiation.

The Planck radiation law describes the intensity and distribution of black body radiation emitted at different wavelengths at a given temperature. At higher temperatures, the intensity of radiation increases, and the peak of the distribution shifts to shorter wavelengths, indicating a shift towards higher-energy photons. As the temperature approaches absolute zero, the radiation intensity decreases, and the peak shifts towards longer wavelengths.

image 3 Black body radiation — As temperatures increase, the intensity of radiation increases, Source: Bodkin Design & Engineering

The Planck radiation law not only provides an accurate description of black body radiation but also plays a crucial role in the development of quantum mechanics. Planck introduced the concept of energy quantization to explain the observed behavior of black body radiation, marking a significant departure from classical physics and paving the way for the development of quantum theory.

Read Also:

Wien’s Displacement Law

Wien’s displacement law, named after the German physicist Wilhelm Wien, is a fundamental relationship that describes the relationship between the wavelength at which the peak intensity of black body radiation occurs and the temperature of the black body. It is a consequence of Planck’s law of black body radiation.

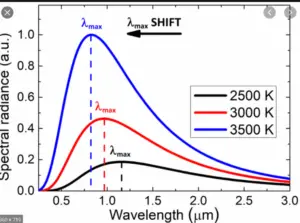
Wien’s displacement law statement: Wien’s displacement law states that the wavelength $(λ_{max})$ at which the peak intensity of radiation occurs is inversely proportional to the temperature $(T)$ of the black body. Mathematically, it can be expressed as:

$$\lambda_{\text{max}} = \frac{b}{T}$$

where:
$λ_{max}$ is the wavelength at which the peak intensity occurs,
T is the temperature of the black body,
b is Wien’s displacement constant, which has a value of approximately $2.898 \times 10^{-3}$ meters per Kelvin.

According to the law, as the temperature of a black body increases, the peak of the radiation spectrum shifts to shorter wavelengths. This means that higher temperatures correspond to higher-energy photons. Conversely, as the temperature decreases, the peak shifts to longer wavelengths, indicating lower-energy photons.

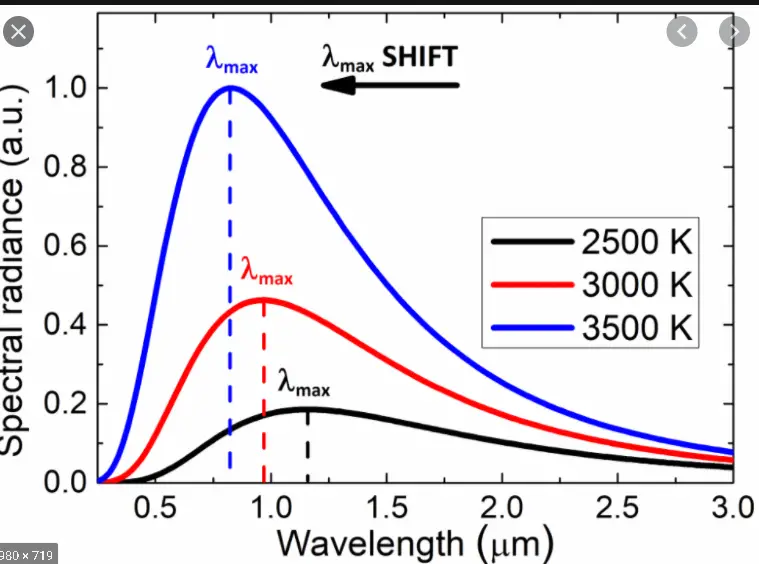
Wien’s displacement law provides a quantitative relationship between the peak wavelength and temperature of black body radiation, allowing scientists to determine the temperature of a black body based on its observed spectral peak. It is an important tool in various fields of physics, such as astrophysics, where the temperature of celestial objects can be estimated by analyzing their radiation spectra.

Stefan-Boltzmann Law

The Stefan-Boltzmann law, named after physicists Josef Stefan and Ludwig Boltzmann, describes the relationship between the total radiant energy emitted by a perfect black body and its temperature. It is a fundamental principle in thermodynamics and plays a crucial role in understanding black body radiation and energy transfer.

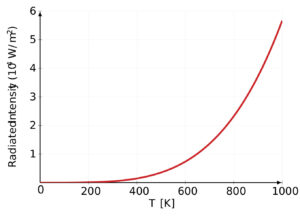
Stefan-Boltzmann law statement: The Stefan-Boltzmann law states that the total power radiated per unit surface area (P) by a perfect black body is directly proportional to the fourth power of its absolute temperature (T). Mathematically, it can be expressed as:

$$P = \sigma \cdot A \cdot T^4$$

where:

P is the total power radiated per unit surface area (in watts per square meter, W/m²),
σ (sigma) is the Stefan-Boltzmann constant, approximately equal to 5.67 × 10^(-8) W/(m²·K⁴),

A is the surface area of the black body, and
T is its absolute temperature measured in Kelvin (K).

According to the Stefan-Boltzmann law, as the temperature of a black body increases, the total power it radiates per unit area increases rapidly. The law quantifies the relationship between temperature and the amount of radiation emitted, emphasizing that hotter objects radiate significantly more energy than cooler objects.

The Stefan-Boltzmann law has numerous applications in astrophysics, including the study of stars, as well as engineering and energy-related fields. It provides insights into the behavior of thermal radiation and facilitates calculations related to energy transfer, heating, and cooling.

Black Body Radiation and Quantum Mechanics

Black body radiation is a phenomenon in which an object at a uniform temperature emits electromagnetic radiation across a wide range of wavelengths. It was initially studied in the late 19th century and played a significant role in the development of quantum mechanics in the early 20th century.

Classically, based on classical physics, the theory of black body radiation predicted that the intensity of radiation emitted by a black body would increase indefinitely as the frequency of the radiation increased, which is known as the ultraviolet catastrophe. This prediction contradicted experimental observations, leading to the need for a new theoretical framework.

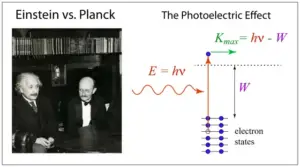
Quantum mechanics, developed by physicists such as Max Planck and Albert Einstein, was introduced to explain the observed behavior of black body radiation. Planck proposed that the energy emitted by the black body is quantized, meaning it can only take on certain discrete values rather than being continuous. He introduced the concept of energy packets, or “quanta,” and derived an expression for the energy of each quantum, which depends on the frequency of the radiation.

Planck’s Quantum Theory class 11: A Comprehensive Guide — Max Planck (energy emitted by the black body is quantized) and Einstein (the energy of each photon is directly proportional to its frequency, and the proportionality constant is Planck’s constant (h)) both contributed to the development of quantum mechanics, Source: Galileo Unbound

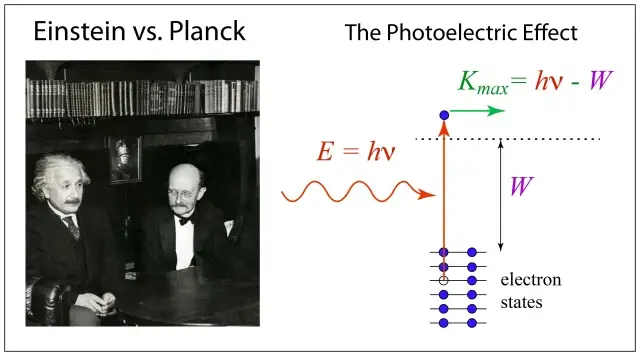
Einstein further contributed to the understanding of black body radiation by proposing the concept of the photon. He suggested that electromagnetic radiation behaves as both particles (photons) and waves. According to Einstein, the energy of each photon is directly proportional to its frequency, and the proportionality constant is Planck’s constant (h). This idea revolutionized our understanding of light and laid the groundwork for the development of quantum mechanics.

The quantization of energy and the concept of photons in black body radiation played a crucial role in the development of quantum mechanics. It challenged classical physics and led to a paradigm shift in our understanding of the behavior of matter and energy at the microscopic level. The principles and mathematical formalism of quantum mechanics have since been applied to various areas of physics, ranging from atomic and molecular physics to solid-state physics and particle physics.

Modern applications of black body radiation

Black body radiation and its principles have various modern applications across scientific and technological fields. Here are some applications of black body radiation:

Astrophysics and Cosmology: Black body radiation is extensively used in the study of stars, galaxies, and the cosmic microwave background radiation. It helps determine the temperature and composition of celestial objects and provides insights into the early universe.
Thermal Imaging: Black body radiation principles are applied in thermal imaging technology. Infrared cameras detect and measure the radiation emitted by objects to create images that depict variations in temperature. This technology has applications in medical diagnostics, building inspections, military surveillance, and more.
Climate Science: The study of black body radiation is crucial for understanding Earth’s energy balance and climate. It helps in modeling and predicting the radiative properties of greenhouse gases, such as carbon dioxide, and their impact on global warming.
Lighting and Energy Efficiency: The principles of black body radiation are utilized in designing efficient lighting sources. Incandescent light bulbs, for example, operate by heating a filament to high temperatures, causing it to emit visible light. By understanding the spectral distribution of the emitted light, lighting technologies can be optimized for energy efficiency and color rendering.
Radiation Therapy: In medical applications, black body radiation principles are employed in radiation therapy for cancer treatment. High-energy photons are used to target and destroy cancer cells based on their interactions with tissue and the principles of energy transfer.
Solar Energy: Black body radiation concepts are relevant to the design of solar panels and solar thermal systems. Understanding the radiation emitted by the Sun and the absorption properties of materials helps optimize the efficiency of solar energy conversion.
Materials Science: The understanding of black body radiation contributes to the field of materials science, particularly in areas such as thermal engineering, heat transfer, and the development of advanced materials for high-temperature applications.

These are only a few examples of how we use black body radiation principles in modern applications. The knowledge and mathematical models we’ve developed from studying black body radiation are still being used in many different scientific and technological fields.

Read Also

Frequently Asked Questions (FAQs)

What is black body radiation in simple terms?

Black body radiation is the heat or light that an object emits because it’s hot. Think of it as the glow you see when you heat a piece of metal until it turns red or when a toaster element becomes red-hot.

Why is it called “black body” radiation?

It’s called “black body” because it’s like a perfect absorber; it soaks up all the heat and doesn’t reflect any light. It looks completely black, even though it’s emitting heat.

How does temperature affect black body radiation?

When something gets hotter, it gives off more intense and brighter heat or light. So, the hotter a black body is, the more intense and colorful its radiation becomes.

Can you see black body radiation in everyday life?

Yes, you can! When you see a red or orange glow from something hot, like a stovetop coil or a piece of metal being heated, that’s black body radiation. It’s all around us in various forms, especially when things get really hot.

What is the significance of the ultraviolet catastrophe in black body radiation?

The ultraviolet catastrophe refers to the incorrect prediction of classical physics that the intensity of black body radiation would increase indefinitely at higher frequencies. The experimental observations contradicted this prediction and led to the realization that classical physics couldn’t explain the behavior of black body radiation, ultimately necessitating the development of quantum mechanics.