Alternating current (AC) is a type of electrical current that periodically reverses its direction, unlike direct current (DC), which only flows in one direction.
We’ve read about electrical circuits that contain a resistor connected across an AC power source, an inductor connected across an AC source, a capacitor connected across an AC source, or a combination of two or all three components connected across an AC source. We know that in the device as a resistance, the current through the resistor is in phase with the voltage source.
But the current lags behind or leads the source voltage to a specific value for devices like inductors or capacitors. This phasor theory relates current and voltage in the latter case. In this section, we will learn to the representation of AC current and voltage by phasor diagram in detail, so let’s get started…
Representation of AC current and voltage by phasor diagram
What is phasor?
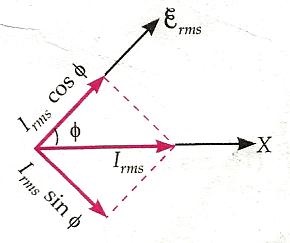
A phasor is a vector used to represent a sine function. It rotates around the origin with the angular velocity ω. The vertical component of the phasors represents the sinusoidally varying magnitudes for a given equation, such as v and i.
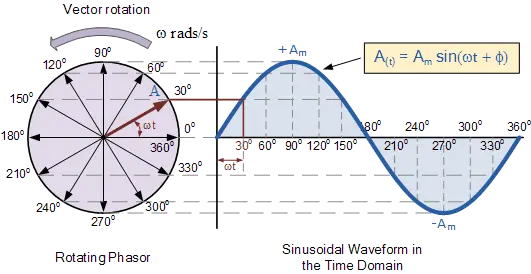
Here the magnitude of the phasor represents the peak value of the voltage and current. From the figure shown above, we can see the relationship between a phasor and the sinusoidal representation of the function with respect to time.
The projection of the phasor onto the vertical axis represents the value of the quantity. For example, in the case of a vector current or phasor, the projection of the phasor onto the vertical axis, given by $v_m\sin\omega t$ and $i_m\sin\omega t$ respectively, gives the value of the current or voltage at that instant.
Read Also
- Phasor and phasor diagram class 12
- Expression for the RMS value of an alternating EMF
- Alternating current class 12 – amplitude, time period, frequency
It is easy to see from the phasor diagram that one of the two quantities is in the same phase. For example, if for a given circuit the phasors for voltage and current are in the same direction in all cases, then the phase angle between voltage and current is zero.
Watch this video for more reference.
Frequently Asked Questions – FAQs
What is a phasor representing current and voltage in phasor form?
Phasor Representation AC is a rotating vector which is a scaled line whose length reflects an AC quantity with both magnitude (“peak amplitude”) and direction (“phase”) that is “frozen” at a specific point in time
How phasor is represented?
A phasor representation is represented as a complex number that is functional in a sinusoidal manner. The time-invariant parameters are amplitude (A), initial phase (θ), and angular velocity (ω). This representation is based upon the concept known as analytic representation
What is meant by a phasor?
In physics and engineering, a phasor (a portmanteau of phase vector) is a complex number representing a sinusoidal function whose amplitude (A), angular frequency (ω), and initial phase (θ) are time-invariant.
Why do we use phasors?
Phasors are rotating vectors having the length equal to the peak value of oscillations, and the angular speed equal to the angular frequency of the oscillations. They are helpful in depicting the phase relationships between two or more oscillations. They are also a useful tool to add/subtract oscillations
What is phasor analysis?
Phasor analysis is a technique to find the steady-state response when the system input is a sinusoid. That is, phasor analysis is a sinusoidal analysis. Phasor analysis is a powerful technique with which to find the steady-state portion of the complete response. Phasor analysis does not find the transient response.
Stay tuned with Laws Of Nature for more useful and interesting content.