In this article, we will discuss alternating current class 12, its amplitude, time period, and frequency, so let’s get started…
What is an alternating current?
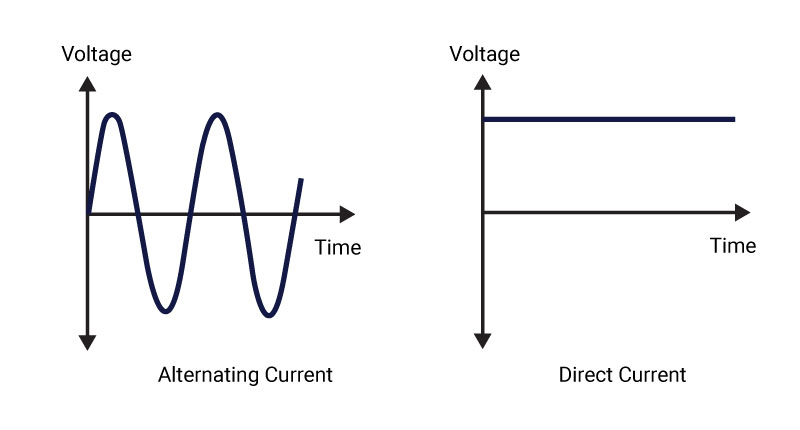
Alternating current (AC) definition: An alternating current (AC) is an electric current that periodically reverses its direction and continuously changes its magnitude over time, unlike a direct current (DC), which flows in only one direction.
Alternating current is the way electrical power is delivered to businesses and homes and in the form of electrical energy that consumers typically use when they plug kitchen appliances, televisions, fans, and electric lights into a wall outlet. A common DC source is a battery cell in a flashlight.
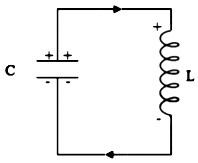
We know that when a coil is rotated in an external magnetic field, an alternating emf is induced in it, which is given by the relation $$\mathcal{E}=\mathcal{E}_0\sin\omega t$$ Suppose this emf is applied to the circuit of resistance $R$, then by the Ohm’s Law, the current in the circuit will be $$I=\frac{\mathcal{E}}{R}=\frac{\mathcal{E}_0}{R}\sin\omega t$$ Or $$I=I_0\sin\omega t$$Thus, current in the circuit varies sinusoidally with time and is called alternating current.
Here, $I$ is the instantaneous value of AC at any instant of $t$, and $\displaystyle{I_0=\frac{\mathcal{E_0}}{R}}$ is the peak or maximum value of AC, and it is called the current amplitude.
Read Also
AC generator – working principles, construction, parts, and induced EMF
Amplitude of an alternating current
The maximum value attend by an alternating current in either direction is called its amplitude or peak value. It is denoted by $I_0$. The formula of amplitude of alternating current is given below: $$\displaystyle{I_0=\frac{\mathcal{E_0}}{R}}$$
Time period of an alternating current
The time taken by an alternating current to complete one cycle of its variations is called its time period and denoted by $T$.
This time is equal to the time taken by the coil to complete one rotation in a magnetic field. As the angular velocity of the coil is $\omega$ and its angular displacement in one complete cycle are $2\pi$, so the time period is given as below:
| $$\displaystyle\text{Time period}=\frac{\text{Angular displacement in a complete cycle}}{\text{Angulat velocity}}$$ Or $$T=\frac{2\pi}{\omega}$$ |
Frequency of an alternating current
The number of cycles completed per second by an alternating current is called its frequency, and it is denoted by $f$.
The frequency of an alternating current is the same as the frequency of the rotation of the coil in an external magnetic field. Thus, $$f=\frac{1}{T}=\frac{\omega}{2\pi}$$ So an alternating current can be expressed as
| $$I=I_0\sin\omega t=I_0\sin 2\pi ft = I_0\sin\frac{2\pi}{T}t$$ |
The figure above shows the variations of alternating current with time $t$. It rises from zero to the maximum in one direction and then falls to zero, again it rises from zero to the maximum in the negative direction, and falls to zero. This way it completed one complete cycle.
Read Also
Methods of producing induced emf Class 12
The alternating current that supply to our houses has the frequency of 50 cps or 50 Hz.
As the alternating current is positive in the first half cycle and equally negative in the second half cycle, its mean value over a complete cycle is zero. Its mathematical proof is given below.
Average value of AC over a complete cycle
The average value of AC over one complete cycle. The alternating current at any instant $t$ is given by $$ I=I_{0} \sin \omega t $$ Assuming the current remains constant for a small time $d t$, then the amount of charge that flows through the circuit in small time $d t$ will be $$ d q=I d t=I_{0} \sin \omega t. d t $$ The total charge that flows through the circuit in one complete cycle of AC.
| $$ \begin{aligned} q &=\int d q=\int_{0}^{T} I_{0} \sin \omega t d t \\ &=I_{0}\left[\frac{-\cos \omega t}{\omega}\right]_{0}^{T}=-\frac{I_{0}}{2 \pi / T}\left[\cos \frac{2 \pi}{T} t\right]_{0}^{T} \\ &=-\frac{I_{0} T}{2 \pi}[\cos 2 \pi-\cos 0]=-\frac{I_{0} T}{2 \pi}[1-1]=0 \end{aligned} $$ |
The average value of a.c. over one complete cycle of a.c., $$ I_{a v}=\frac{q}{T}=\mathbf{0} $$ Thus the average value of a.c. over a complete cycle of a.c. is zero.
Stay tuned with Laws Of Nature for more useful and interesting content.