Power factor class 12 – definition, and formula

In this article, we will discuss the Power factor class 12 – definition, and formula. So let’s get started…

Understanding power factor using Beer Mug Analogy

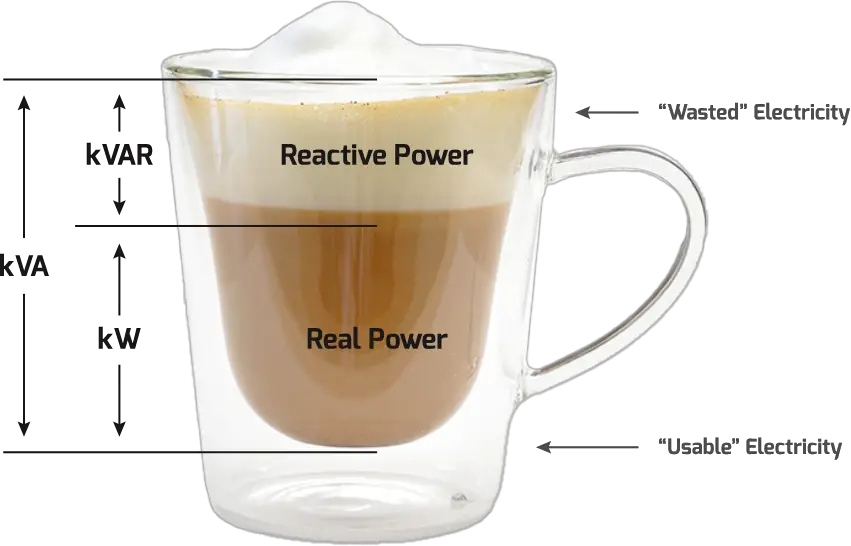
Let’s say, you are in the park with your friends, and its a summer time. Your friends decided to order a mug of cold beer, and they ordered. When they started pouring into the glass. You must have seen that there is some foam on the upper part of the glass, and real drinkable beer is in the lower part of the glass. We will use this beer glass for understanding the power factor of the electrical system.

To understand the power factor in an electrical system, we must first understand some basic terms used in an electrical system, which are detailed below.

• kW: Work power (also called real power, active power, or active power). Power):- It is the power that actually powers the device and does useful work.
• kVAR – Reactive Power:- It is the power required by the magnetic device (transformer, induction motor, and relay) to create the magnetizing flux.
• kVA – Apparent Power:- It is the “Vector Sum” of KVAR and KW.

Don’t get confused with these terms, Let”s understand them with the beer mug analogy.

• The thirst-quenching part of their beer is represented by KW. This is usable energy.
• Some foam will come along with your beer. (And that foam just won’t quench your thirst.) That foam is represented by KVAR. This part is wasted energy.
• The total volume of your mug, KVA, is the sum of KW (the beer) and KVAR (the foam).

So we have some basic concepts of the beer mug analogy. Now we’re ready to learn about power factor:

From the beer glass mug analogy, the power factor is given as:

Power Factor (Cos Φ) is the ratio of Working Power (True Power) to Apparent Power. $$PF = \frac{KW}{KVA}$$

\begin{aligned}\cos\phi=PF &= \frac{KW}{(KW + KVAR)}\\ \cos\phi &= \frac{\text{Beer}}{(\text{Beer} +\text{Foam})}\end{aligned}

So, for a given KVA:

• The more foam you have (higher KVAR percentage), the lower the ratio of KW (beer) to KVA (beer plus foam). Therefore, the power factor is all the lower.
• The less foam you have (the lower the KVAR percentage), the higher your KW (beer) to KVA (beer plus foam) ratio.
• The closer your foam (or KVAR) gets to zero, the closer your power factor gets to 1.

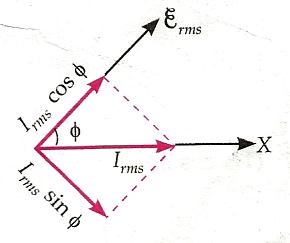
Power Triangle

A triangle that illustrates the relationship between KW, KVA, KVAR, and Power Factor is called a power triangle.

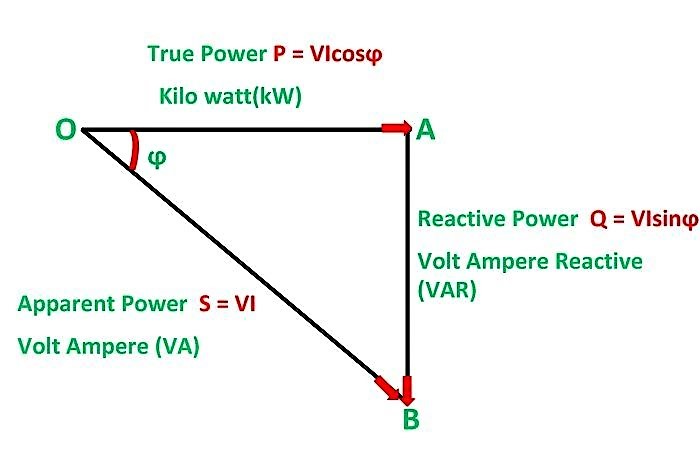
If each component of the current, which is the active component (Icosϕ) or the reactive component (Isinϕ), is multiplied by the voltage V, a power triangle is obtained, shown in the figure above:

• The power actually consumed or used in an AC circuit is called real power, real power, or active power. It is measured in kilowatts (kW) or MW.
• The power that flows from one side to the other means that it moves in both directions in the circuit or acts back on it, it is called reactive power. Reactive power is measured in kilovolt-amperes reactive (kVAR) or MVAR.
• The product of the root means square (RMS) of voltage and current is called apparent power. This power is measured in KVA or MVA.

The next point shows the relationship between the following quantities and is explained using the power triangle graph shown above

What is Power Factor?

The average power of an AC the circuit is given by
$$P_{a v}=\varepsilon_{r m s} \cdot I_{r m s} \cos \phi$$
Average power

$$\text{Average power}= \text{Virtual emf} \times \text{Virtual current} \times \cos \phi$$

The product $\varepsilon_{rms}. I_{r m s}$ does not give the actual power and is called apparent power. It gives actual or true power only when multiplied by factor $\cos \phi$. The factor $\cos \phi$ is called the power factor of an a.c. circuit.

$$\therefore \text{True power} = \text{Apparent power} \times \text{power factor}$$

Read Also

• Sharpness of Resonance: Q-Factor in LCR circuit, class 12
• Power in an AC circuit: definition, and formula derivation
• Choke coil – principle, working, and construction, class 12
• Resonance condition in a series LCR circuit
• AC voltage applied to a series LCR circuit

Power factor definition

Power factor definition: Power factor may be defined as the ratio of the true power to the apparent power of an a.c. circuit. $$\text{Power factor}=\frac{\text{True power}}{\text{Apparent power}}$$

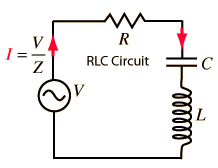
Its value varies from 0 to 1. The power factor of a series $L C R$-the circuit is given by
$$\cos \phi=\frac{R}{Z}=\frac{R}{\sqrt{R^2+(\omega L-1 / \omega C)^2}}$$

Where:

• R = Resistance in Ohms (Ω)
• Z = Impedance (Resistance in AC circuits i.e. X_L, X_C, and R known as Inductive reactance, capacitive reactance, and resistance respectively) in Ohms (Ω)
• Cosθ = Power factor

The ratio between Resistance and Impedance in AC Circuit is known as Power Factor.

For a purely inductive or capacitive circuit, $\phi=90^{\circ}$

$\therefore$ Power factor $=\cos 90^{\circ}=0$.
Thus the power factor assumes the minimum value for a purely inductive or capacitive circuit.

For a purely resistive circuit, $\phi=0^{\circ}$.
$\therefore$ Power factor $=\cos 0^{\circ}=1$.

Thus the power factor assumes the maximum value for a purely resistive circuit.

Read Also

• AC circuit containing an inductor only
• AC circuit containing resistor only, class 12
• Representation of AC current and voltage by phasor diagram
• AC circuit containing resistor and inductor in series

Power factor calculator

Frequently Asked Questions – FAQs

Stay tuned with Laws Of Nature for more useful interesting content.