In this article, we will discuss the Power of an AC circuit: definition, and formula derivation, so let’s get started…
Power in an AC circuit
Power in an AC circuit definition: The rate at which electric energy is consumed in an electric circuit is called its power.
In a DC circuit, power is given by the product of voltage and current. But in an AC circuit, both voltage $\varepsilon$ and current $I$ vary sinusoidally with time and are generally not in phase: So for an AC circuit, we define instantaneous power as the product of the instantaneous voltage and instantaneous current.
Suppose in an a.c. circuit, the voltage, and current at any instant are given by
$$\varepsilon=\varepsilon_0 \sin \omega t \text { and } I=I_0 \sin (\omega t-\phi)$$
where $\phi$ is the phase angle by which the voltage $\varepsilon$ leads the current $I$.
Read Also
Power in an AC circuit derivation
The instantaneous power is given by
$$\begin{aligned}
P=& \varepsilon_I=\varepsilon_0 I_0 \sin \omega t \cdot \sin (\omega t-\phi) \\
=& \frac{\varepsilon_0 I_0}{2}[2 \sin \omega t \cdot \sin (\omega t-\phi)] \\
=& \frac{\varepsilon_0 I_0}{2}[\cos \phi-\cos (2 \omega t-\phi)] \\
[\because 2 \sin A \sin B&=\cos (A-B)-\cos (A+B)]
\end{aligned}$$
Average power dissipated per cycle
$$=\text { Average of } \frac{\varepsilon_0 I_0}{2}[\cos \phi-\cos (2 \omega t-\phi)] \text {. }$$
The second cosine term $[\cos (2 \omega t-\phi)]$ is time-dependent. Its average over a cycle is zero.
$$\therefore \quad P_{a v}=\frac{\varepsilon_0 I_0}{2} \cos \phi$$
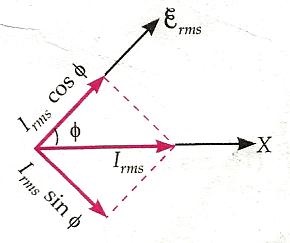
or$$P_{a v}=\frac{\varepsilon_0}{\sqrt{2}} \cdot \frac{I_0}{\sqrt{2}} \cdot \cos \phi$$or$$P_{a v}=\varepsilon_{r m s} I_{r m s} \cos \phi=\varepsilon_{r m s} I_{r m s} \cdot \frac{R}{Z}$$
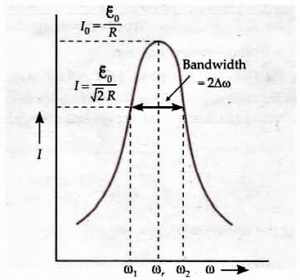
| Special Cases 1). Pure resistive circuit. Here the voltage and current are in same phase, i.e., $\phi=0$ and $\cos \phi=1$. $$\therefore \quad P_{a v}=\varepsilon_{r m s} \cdot I_{r m s} \times 1=\varepsilon_{r m s} \cdot I_{r m s}=\frac{\varepsilon_{r m s}^2}{R}$$ 2). Pure inductive circuit. Here the voltage leads the current in phase by $\frac{\pi}{2}$, i.e., $\phi=\frac{\pi}{2}$. $$\therefore \quad P_{a v}=\varepsilon_{r m s} . I_{r m s} \cos \frac{\pi}{2}=0$$ Thus the average power consumed in an inductive circuit over a complete cycle is zero. 3). Pure capacitive circuit. Here the voltage lags behind the current in phase by $\frac{\pi}{2}$, i.e., $\phi=-\frac{\pi}{2}$. $$\therefore \quad P_{a v}=\varepsilon_{r m s} \cdot I_{r m s} \cos \left(-\frac{\pi}{2}\right)=0$$Thus the average power consumed in a capacitive circuit over a complete cycle is also zero. 4). Series LCR-circuit. For a series LCR-circuit, $P_{a v}=\varepsilon_{r m s} I_{r m s} \cos \phi$, where $\phi=\tan ^{-1} \frac{X_L-X_C}{R}$. Sometimes, $\phi$ may have a non-zero value for series LR-, LC and LCR-circuits. So power is consumed in such circuits, but only in the resistor $R$. 5). The power dissipated at resonance in the LCR circuit. At resonance, $X_L=X_C$, and $\phi=0$. So $\cos \phi=1$, and $P_{a v}=\varepsilon_{r m s} I_{\text {rms }}$. At resonance, maximum power is dissipated in the circuit (through $R$). |
Read Also
- AC circuit containing an inductor only
- AC circuit containing resistor only, class 12
- Representation of AC current and voltage by phasor diagram
- AC circuit containing resistor and inductor in series
Stay tuned with Laws Of Nature for more useful interesting content.