Sharpness of Resonance: Q-Factor in LCR circuit, class 12

In this article, we will discuss the sharpness of resonance: Q-factor in LCR circuits. So let’s get started…

What is resonance?

We can understand the sharpness of a resonance better by understanding the term resonance. Resonance describes the phenomenon of increasing amplitude that occurs when the frequency of an applied periodic force is at or near the natural frequency of the system on which it acts.

The frequency at which resonance occurs is called resonant frequency. At the resonant frequency, the amplitude of the system is relatively maximum. The Q factor is used to define the sharpness of the resonance.

Read Also

• Resonance condition in a series LCR circuit

The sharpness of resonance

The time depletion of an oscillating wave is called resonance sharpness. It is related to the decrease in energy that occurs in an oscillating system. It is mainly determined by the Q-factor The sharpness of the resonance depends mainly on two factors. These are

• Amplitude
• Damping

Amplitude: It is defined as the height of a wave moving with a uniform motion. The amplitude varies inversely with the sharpness of the resonance. The higher the amplitude, the less sharp the resonance. The smaller the amplitude, the sharper the resonance.

Damping: It is defined as the effect where the amplitude of the wave decreases over time. It can be both artificial and natural. The damping is directly related to the sharpness of the resonance. Increasing the damping leads to an increase in the sharpness of the resonance and vice versa.

Q-Factor

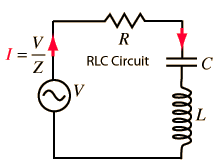
The below figure shows the variation of current amplitude $I_0$ in a series LCR-circuit with angular frequency $\omega$, for three different values of $R$. The current amplitude has a peak at the resonant frequency $\omega_r=\frac{1}{\sqrt{L C}}$ and falls to zero in either direction.

The resonant frequency is independent of $R$, but the sharpness of the peak depends on $R$. The peak is higher for smaller values of $R$. Thus the resonance is sharp for small $R$ and flat for large $R$. The sharpness of resonance is measured by a coefficient called the quality or Q-factor of the circuit.

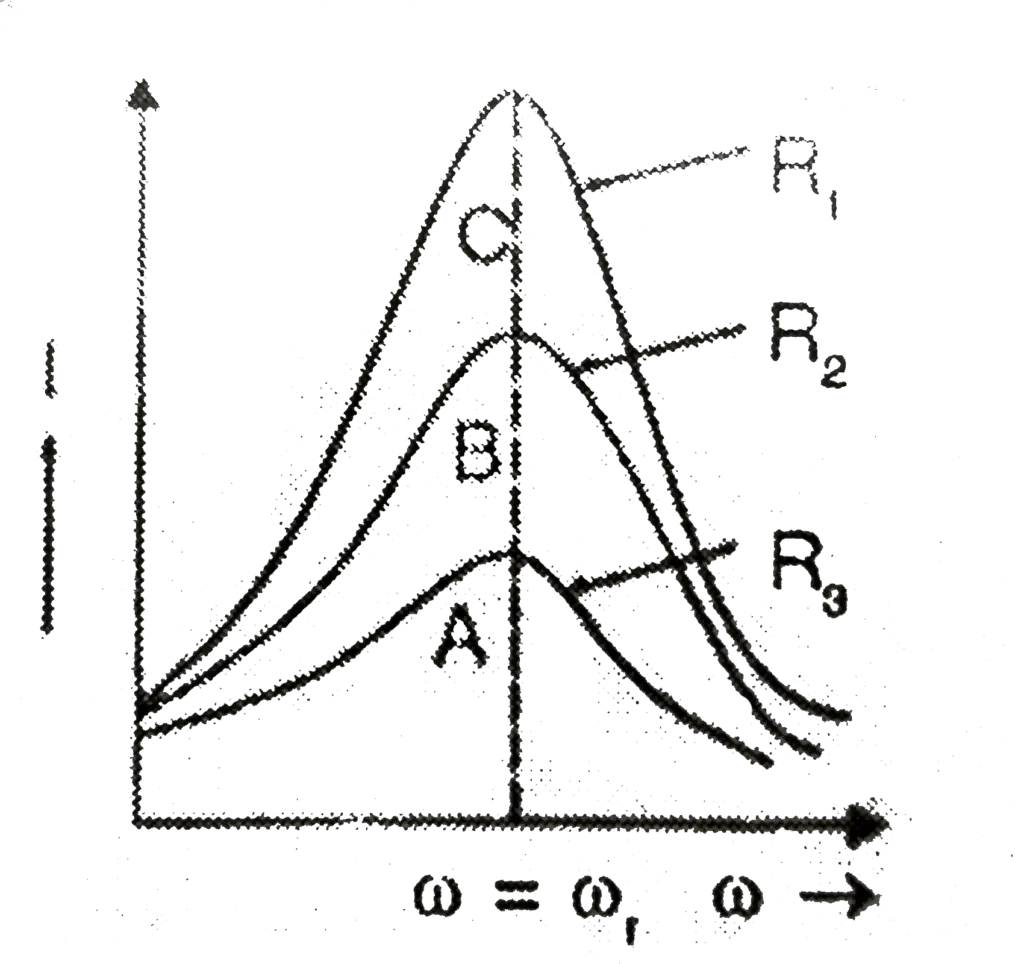
Q-Factor definition

Q-Factor definition: The Q-factor of a series resonant circuit is defined as the ratio of the resonant frequency to the difference in two frequencies taken on both sides of the resonant frequency such that at each frequency, the current amplitude becomes $\frac{1}{\sqrt{2}}$ times the value at a resonant frequency.

Mathematically, the $Q$-factor can be expressed as

where $\omega_1$ and $\omega_2$ are the frequencies at which the current falls to $\frac{1}{\sqrt{2}}$ times its resonant value, as shown in below figure, and we have used$$\omega_1=\omega_r-\Delta \omega ; \quad \omega_2=\omega_r+\Delta \omega$$

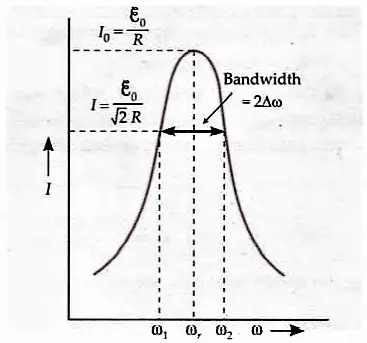
The frequency range $\omega_2-\omega_1=2 \Delta \omega$ is called bandwidth. The larger the value of $Q$-factor, the smaller the value of $2 \Delta \omega$ or the bandwidth, and the sharper the peak in the current. $Q$-factor is a dimensionless quantity.

Read Also

• Representation of AC current and voltage by phasor diagram
• AC circuit containing resistor and inductor in series
• AC voltage applied to a series LCR circuit

Derive an expression for $Q$-factor

Clearly at $\omega_r$, the impedance is equal to $R$, while at $\omega_1$ and $\omega_2$ its value is $\sqrt{2} R$.
$$\therefore \quad Z=\sqrt{R^2+\left(\omega L-\frac{1}{\omega C}\right)^2}=\sqrt{2} R$$
or $\quad R^2+\left(\omega L-\frac{1}{\omega C}\right)^2=2 R^2$ or $\omega L-\frac{1}{\omega C}=\pm R$

We can write$$\begin{aligned}&\omega_1 L-\frac{1}{\omega_1 C}=-R \qquad ….(1)\\
&\omega_2 L-\frac{1}{\omega_2 C}=+R\qquad ….(2)\end{aligned}$$Adding (1) and (2), we get$$
\left(\omega_1+\omega_2\right) L-\frac{1}{C}\left(\frac{\omega_1+\omega_2}{\omega_1 \omega_2}\right)=0$$or$$\omega_1 \omega_2=\frac{1}{L C}$$Subtracting (1) from (2), we get $$\left(\omega_2-\omega_1\right) L+\frac{1}{C}\left(\frac{\omega_2-\omega_1}{\omega_1 \omega_2}\right)=2 R$$or$$\left(\omega_2-\omega_1\right)\left(L+\frac{1}{C \omega_1 \omega_2}\right)=2 R$$or$$\left(\omega_2-\omega_1\right)(L+L)=2 R\left[\because \omega_1 \omega_2=\frac{1}{L C}\right]$$ or \begin{aligned}\omega_2-\omega_1 &=\frac{R}{L} \\
\therefore \quad Q=\frac{\omega_r}{2 \Delta \omega}&=\frac{\omega_r}{\omega_1-\omega_2}=\frac{\omega_r L}{R}\qquad …. (3)\end{aligned}

The above equation can also be written as

Thus the Q-factor of a series LCR circuit may also be defined as the ratio of the voltage drop across the inductance (or capacitance) at resonance to the applied voltage.

As $\quad \omega_r=\frac{1}{\sqrt{L C}}$
$\omega_r^2=\frac{1}{L C} \quad$ or $\quad \omega_r L=\frac{1}{\omega_r C}$
Using the above relations, we get
$$Q=\frac{1}{\omega_r C R}=\frac{1}{R} \sqrt{\frac{L}{C}}$$

From equation (3), we see that if $Q$-factor is large i.e. if $R$ is low or Lis large, the bandwidth $2 \Delta \omega$ is small. This means that the resonance is sharp or the series resonant circuit is more selective.

Tuning of a radio receiver

The tuning circuit of a radio or TV is an example of a $L C R$ resonant circuit. Signals are transmitted by different stations at different frequencies. These frequencies are picked up by the antenna and corresponding to these frequencies, a number of voltages appear across the series LCR-circuit.

But maximum current flows through the circuit for that a.c. voltage which has frequency equal to $f_r=\frac{1}{2 \pi \sqrt{L C}}$. If the Q-value of the circuit is large, the signal of the other station will be very weak. By changing the value of the adjustable capacitor $C$, the signal from the desired station can be tuned in.

Frequently Asked Questions – FAQs

Stay tuned with Laws Of Nature for more useful and interesting content.