This article will discuss the Wattless current class 12, so let’s get started…
Wattless current
Wattless current: The current in a.c. the circuit is said to be wattless if the average power consumed in the circuit is zero. The average power of an a.c. the circuit is given by
$$P_{a v}=\varepsilon_{r m s} I_{r m s} \cos \phi$$
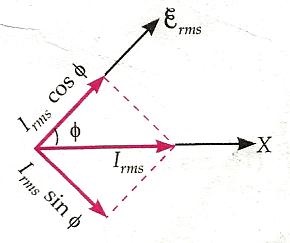
The above figure shows the phase angle $\phi$ between $\varepsilon_{r m s}$ and $I_{r m s}$. The current $I_{r m s}$ can be resolved into two components:
(a) Component $I_{r m s} \cos \phi$ along $\varepsilon_{r m s}$. As the phase angle between $I_{r m s} \cos \phi$ and $\varepsilon_{r m s}$ is zero, therefore $$P_{a v}=\varepsilon_{r m s}\left(I_{r m s} \cos \phi\right) \cos 0=\varepsilon_{r m s} I_{r m s} \cos \phi$$
(b) Component $I_{r m s} \sin\phi$ normal to $\varepsilon_{r m s}$. As the phase angle between $I_{r m s} \sin \phi$ and $\varepsilon_{r m s}$ is $\frac{\pi}{2}$, therefore
$$
P_{a v}=\varepsilon_{r m s}\left(I_{r m s} \sin \phi\right) \cdot \cos \frac{\pi}{2}=0
$$
We call the component $I_{r m s} \sin \phi$ as the idle or wattless current because it does not consume any power in a.c. circuit. This happens in a purely inductive or capacitive circuit in which the voltage and current differ by a phase angle of $\frac{\pi}{2}$, i.e., $\phi=\pm \frac{\pi}{2}$, so that
$$
P_{a v}=\varepsilon_{r m s} I_{r m s} \cos (\pm \pi / 2)=0
$$
Thus the current in the circuit has no power. It flows sometimes along the voltage and sometimes against the voltage so that the net work done per cycle is zero. For example, when the secondary of a transformer is open, the current in the primary is almost wattless.
Read Also
- Sharpness of Resonance: Q-Factor in LCR circuit, class 12
- Power in an AC circuit: definition, and formula derivation
- Choke coil – principle, working, and construction, class 12
- Resonance condition in a series LCR circuit
- AC voltage applied to a series LCR circuit
Stay tuned with Laws Of Nature for more useful interesting content.