Resonance condition in a series LCR circuit

In this article, we will discuss the resonance condition in a series LCR circuit, so let’s get started…

What is resonance? A simple explanation

Before moving on to the topic of resonance conditions in series LCR circuits. It is necessary for us that we understood the term “resonance“. So what is resonance?

Let’s take the example of swing to understand the phenomenon of resonance. Whenever a person is swinging on a swing, then he is swinging with a system’s frequency called natural frequency.

Actually, everything in this universe is vibrating (oscillating) with its base frequency without any driving force, this base or system’s frequency is called the natural frequency. More formal, natural frequency can be defined as:

Natural frequency definition: Natural frequency, also known as eigenfrequency, is the frequency at which a system tends to oscillate in the absence of any driving force.

Now come on to the example of the swing, if anyone pushes the person from behind (as normally does) if the frequency of his pushes matches the swing’s natural frequency, then the person on the swing goes to a very high altitude. Swing amplitude becomes very high. The phenomenon of high amplitude that happened with the swing after pushing it from behind is called resonance.

Resonance definition: Resonance describes the phenomenon of increasing amplitude that occurs when the frequency of an applied periodic force is at or near the natural frequency of the system on which it acts.

When an oscillating force is applied at one resonant frequency of a dynamic system, the system vibrates with a greater amplitude than when the same force is applied at other non-resonant frequencies.

Now let’s talk about the resonance condition in a series LCR circuit.

Read Also

• AC circuit containing an inductor only
• AC circuit containing resistor only, class 12

Resonance condition in a series LCR circuit

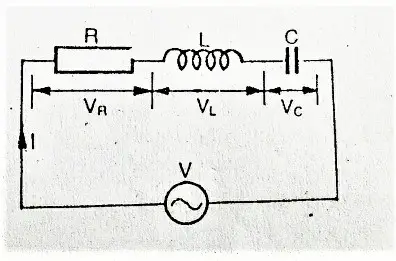
Resonance occurs when the value of the inductive and capacitive reactances have the same magnitude but a phase difference of 180°. In other words, the point at which X_L = X_C occurs is called the resonant frequency point (ƒ_r) of the circuit, and since we are considering a series RLC circuit, this resonant frequency creates a series resonance.

In this state, they cancel each other out. The state at which they cancel out each other is known as the resonant state of a series LCR circuit. Therefore the circuit is called an LCR resonant circuit.

Behavior of inductor and capacitor over varying frequency

The value of an inductor’s inductive reactance increases linearly as the frequency across it increases. Therefore, inductive reactance is positive and directly proportional to frequency (X_L ∝ ƒ). The same is true for the capacitive reactance formula above but in reverse.

If the frequency or capacitance is increased, the total capacitive reactance would decrease. As the frequency approaches infinity, the reactance of the capacitors would drop to almost zero, allowing the circuit element to act as a perfect 0Ω conductor.

However, as the frequency approaches zero, the reactance of the capacitors would quickly increase to infinity, causing them to act as a very large resistance and becoming more of an open circuit condition. This means that the capacitive reactance is “inversely proportional” to the frequency for any given capacitance value.

The values ​​of these resistances depend on the frequency of the supply. At higher frequencies, X_L is high and at lower frequencies, X_C is high. So there must be a frequency point where the value of X_L is the same as the value of X_C.

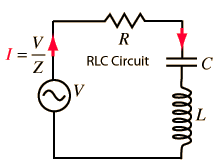
Derivation for resonant frequency in series LCR circuit

The resonance condition of a series $LCR$-circuit: A series LCR-circuit is said to be in the resonance condition when the current through it has its maximum value. The current amplitude $I_0$ for a series LCR circuit is given by
$$
I_0=\frac{E_0}{\sqrt{R^2+\left(\omega L-\frac{1}{\omega C}\right)^2}}
$$
Clearly, $l_0$ becomes zero both for $\omega \rightarrow 0$ and $\omega \rightarrow \infty$. The value of $I_0$ is maximum when
$$
\omega L-\frac{1}{\omega C}=0 \quad \text { or } \quad \omega=\frac{1}{\sqrt{L C}}
$$
Then, the impedance, $Z=\sqrt{R^2+\left(\omega L-\frac{1}{\omega C}\right)^2}=R$
Clearly, the impedance is minimum. The circuit is purely resistive. The current and voltage are in the same phase and the current in the circuit is maximum This condition of the LCR circuit is called the resonant condition. The frequency at which the current amplitude $I_0$ attains a peak value is called the resonant frequency of the $L C R$-circuit and is denoted by $f_{\text {. }}$.
Thus, $$\omega_r=2 \pi f_r=\frac{1}{\sqrt{L C}} \; \text{or}\; f_r=\frac{1}{2 \pi \sqrt{L C}}$$. The current amplitude at resonant frequency will be
$$
l_0=\frac{\mathcal{E}_0}{R} .
$$

Characteristics of a series resonant circuit

Characteristics of the series resonant circuit:

1. Resonance occurs in a series of LCR-circuit when
   $$
   X_L=X_C \text {. }
   $$
2. Resonant frequency, $$f_r=\frac{1}{2 \pi \sqrt{L C}}$$.
3. The impedance is minimum and purely resistive.
4. The current has a maximum value of $\left(\varepsilon_0 / R\right)$ at resonant condition.
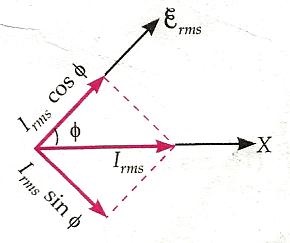
5. The power dissipated in the circuit is maximum and is equal to $\varepsilon_{r m s}^2 / R$.
6. The current is in phase with the voltage or the power factor is unity $(\cos \phi=1$ when $\phi=0$ ).
7. Series resonance can occur at all values of resistance $R$.
8. The voltage across $R$ is equal to the applied emf.
9. The voltages across $L$ and $C$ are equal and have a phase difference of $180^{\circ}$ and so their resultant is zero.
10. The voltages across $L$ and $C$ are very high as compared to the applied voltage. Hence a series $L C R$-the circuit is used to obtain a large magnification of a.c. voltage.
11. The series resonant circuit is also called an acceptor circuit. When a number of frequencies are fed to it, it accepts only one frequency $f_r$ and rejects the other frequencies. The current is the maximum for this frequency.

Read Also

• Representation of AC current and voltage by phasor diagram
• AC circuit containing resistor and inductor in series
• AC voltage applied to a series LCR circuit

Frequently Asked Questions – FAQs

Stay tuned with Laws Of Nature for more useful and interesting content.