In this article, we will discuss the concepts of LC Oscillation class 12, so let’s get started…
What is LC Oscillation?
LC Oscillation Definition: A constant amplitude and frequency are produced when a charged capacitor discharges through a non-resistive inductor. These oscillations are known as LC oscillations.
A qualitative explanation for the production of LC Oscillations
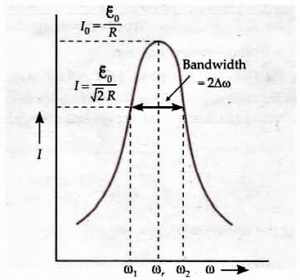
Figure (a) depicts a capacitor connected to an ideal inductor with an initial charge of $q_0$, and $\displaystyle{ U_=\frac {1}{2} \frac{q_0^2}{C}}$ is the electrical energy stored in the charged capacitor. Because there is no current in the circuit, the energy stored in the inductor’s magnetic field is zero.
When the circuit is closed Fig. (b), the capacitor begins to discharge through the inductor, resulting in a current $I$. The magnetic field around the inductor increases as the current $I$ increases. A portion of the capacitor’s electric energy is stored in the inductor as magnetic energy, $\displaystyle{ U_=\frac {1}{2} L I^2}$.
Later Fig. (c), the capacitor is fully discharged, and the potential difference across its plates is zero. The energy stored in the magnetic field is $\displaystyle{\frac{1}{2} L I_0^2}$ when the current reaches its maximum value $I_0$. As a result, the capacitor’s entire electrostatic energy has been converted into the inductor’s magnetic field energy.
When the capacitor is fully discharged, the magnetic flux connected to the inductor decreases, inducing a current in the same direction (Lenz’s law) as the earlier current, as shown in Fig. (d), Thus, the current continues, albeit with decreasing magnitude, and charges the capacitor in the opposite direction.
The inductor’s magnetic energy begins to transform into the capacitor’s electrostatic energy. This procedure is repeated until the capacitor is fully charged (Fig. (e). However, it is charged with the opposite polarity as in its initial state Fig. (a). Thus, the entire energy is stored as $\displaystyle{\frac{1}{2} \frac{q_0^2}{C}}$ in the capacitor’s electric field.
The capacitor begins to discharge again, sending current in opposite direction Fig. (f). The energy is once again transferred to the magnetic field of the inductor. Thus the process repeats in the opposite direction Fig. (g) and (h). The circuit eventually returns to the initial state Fig. (a).
As a result, the system’s energy is constantly bouncing back and forth between the electric field of the capacitor and the magnetic field of the inductor. This causes electrical oscillations with a fixed frequency $f_0$. These are known as LC oscillations. If there is no energy loss, the amplitude of the oscillation remains constant, as illustrated in the figure below. These oscillations are known as undamped oscillations.
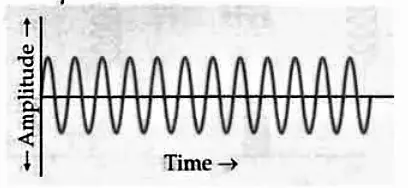
However, the LC oscillations are usually dampened due to the following reasons :
- Every inductor has some level of resistance. This results in energy loss as heat. The amplitude of oscillations continues to decrease, and the oscillations eventually die out.
- Even if the resistance were zero, the system’s total energy would not be constant. It escapes in the form of electromagnetic waves. Indeed, radio and television transmitters rely on such radiation to function.
Mathematical treatment of LC oscillations
Mathematical treatment of LC-oscillations: As shown in Figure below, suppose a capacitor of capacitance $C$, initially charged to $q_{0^{\prime}}$, be connected to an inductor of inductance $L$. As the circuit is closed, the charge on the capacitor begins to decrease, giving rise to a current in the circuit.
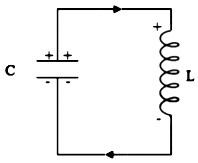
As $q$ decreases, $I$ increases, so $\displaystyle I=-\frac{dq}{dt}$
Induced emf across the inductor at any instant is given as $\displaystyle\mathcal{E}=-L\frac{dI}{dt}$
Potential difference across the capacitor at that instant $\displaystyle=\frac{q}{C}$
According to Kirchhoff’s loop rule,
$$\quad-L \frac{d I}{d t}+\frac{q}{C}=0$$
or
| $$\quad+L \frac{d^2 q}{d t^2}+\frac{q}{C}=0 \quad\left[\because I=-\frac{d q}{d t}, \frac{d I}{d t}=-\frac{d^2 q}{d t^2}\right]$$ |
| \begin{aligned} \text{or}\qquad \frac{d^2 q}{d t^2}+\frac{1}{L C} q&=0\\ \text{or}\qquad\frac{d^2 q}{d t^2}+\omega_0^2 q&=0\end{aligned} where $\displaystyle\omega_0=\frac{1}{\sqrt{L C}}$. This is a linear differential equation of second order. It has a general solution of the form: \begin{aligned} q & =A \cos \omega_0 t+B \sin \omega_0 t \\ \text { At } t=0, \quad q & =q_{0^{\prime}}, \text { so } \\ q_0 & =A \cos 0+B \sin 0 \\ \text{or}\quad A & =q_0 \end{aligned} \begin{aligned} \text{Also}, \quad \frac{d q}{d t}&=-\omega_0 A \sin \omega_0 t+\omega_0 B \cos \omega_0 t\\ \text{At t=0}, \quad q&=q_0\; \text{(maximum)}\; \text{and so}\; \frac{d q}{d t}=0\\ \therefore \quad 0&=-\omega_0 A \sin 0+\omega_0 B \cos 0\\ \text{or}\qquad B&=0\\ \text{Hence} \quad q&=q_0 \cos \omega_0 t\\ \text{and} \quad I&=-\frac{d q}{d t}=\omega_0 q_0 \sin \omega_0 t \end{aligned} Thus the charge on the capacitor plates oscillates simple harmonically with time with angular frequency. $$\omega_0=\frac{1}{\sqrt{L C}}$$Frequency of oscillation, $\displaystyle f_0=\frac{\omega_0}{2 \pi}=\frac{1}{2 \pi \sqrt{L C}}$. |
Conservation of energy in LC oscillations
Conservation of Energy In Lc-Oscillations. Just as the sum of potential and kinetic energies remains constant in SHM, the sum of energies stored in the capacitor and inductor remains constant during LC oscillations. At any instant, the electrostatic energy stored in the capacitor is
$$
U_E=\frac{1}{2} \cdot \frac{q^2}{C}
$$
The magnetic energy stored in the inductor at any instant is
$$
U_B=\frac{1}{2} L I^2
$$
If there is no (resistive) loss of energy, then the total energy of the LC circuit at any instant will be
$$
U=U_E+U_B=\frac{1}{2} \cdot \frac{q^2}{C}+\frac{1}{2} L I^2
$$
But $\displaystyle q=q_0 \cos \omega_0 t$ and $I\displaystyle=-\frac{d q}{d t}=\omega q_0 \sin \omega_0 t$
| $\begin{aligned} \therefore U &=\frac{1}{2 C} \cdot q_0^2 \cos ^2 \omega_0 t+\frac{1}{2} L \omega_0^2 q_0^2 \sin ^2 \omega_0 t \\ &=\frac{1}{2 C} \cdot q_0^2 \cos ^2 \omega_0 t+\frac{1}{2} L \frac{1}{L C} q_0^2 \sin ^2 \omega_0 t \\ &=\frac{1}{2} \cdot \frac{q_0^2}{C}\left[\cos ^2 \omega_0 t+\sin ^2 \omega_0 t\right]=\frac{1}{2} \cdot \frac{q_0^2}{C} \\ &=\frac{1}{2} C V_0^2=\text { Initial energy, as expected } \end{aligned}$ |
Read Also
- Sharpness of Resonance: Q-Factor in LCR circuit, class 12
- Power in an AC circuit: definition, and formula derivation
- Choke coil – principle, working, and construction, class 12
- Resonance condition in a series LCR circuit
- Wattless current class 12
- Expression for energy and average power stored in an inductor
Mechanical Analogy for LC oscillations
The LC oscillations are similar to the oscillations of the mass-spring system. In the $L C$-system, the energy alternates between electrostatic and magnetic forms while in the mass-spring system, it alternates between potential and kinetic forms. The capacitor acts like a spring while the inductor acts like an inertial mass. The charge corresponds to displacement and the current corresponds to velocity.
The displacement $x$ of oscillating mass satisfies the differential equation :
$$
\frac{d^2 x}{d t^2}+\omega_0^2 x=0 \text {, where } \omega_0=\sqrt{\frac{k}{m}}
$$
The charge $q$ of the capacitor satisfies a similar equation :
$$
\frac{d^2 q}{d t^2}+\omega_0^2 q=0 \text {, where } \omega_0=\frac{1}{\sqrt{L C}}
$$
Clearly, $x$ corresponds to $q$.
For a mechanical system,
$$
F=m \frac{d v}{d t}=m \frac{d^2 x}{d t^2}
$$
For an electrical system,
$$
\varepsilon=-L \frac{d I}{d t}=-L \frac{d^2 q}{d t^2}
$$
On comparing the above two equations, we see that $L$ is analogous to mass $m$ i.e., $L$ is a measure of resistance to change in current.
Again, in case of $L C$ system, $$\omega_0=\frac{1}{\sqrt{L C}}$$ In case of mass-spring system, $$\omega_0=\sqrt{\frac{k}{m}}$$ Obviously, $\frac{1}{C}$ is analogous to $k$. The force constant $k$ is the force required to produce unit displacement while $\frac{1}{C}\left(=\frac{V}{q}\right)$ is the potential difference required to store a unit charge.
Analogies between mechanical and electrical quantities

Frequently Asked Questions – FAQs
Define an inductor.
An inductor is a passive component that stores magnetic energy when power is applied to it.
What is a capacitor?
A capacitor is a two-terminal device that can store energy in the form of an electric charge.
What is an LC circuit?
An LC circuit is a type of electric circuit that is made up of an inductor which is expressed by the letter L, and a capacitor, represented by the letter C.
Why does an LC circuit produce oscillation?
Magnetic energy is converted into electrical energy and vice versa. Oscillations are produced as a result of this change.
Why is it called an LC circuit?
An LC circuit is a type of electric circuit composed of an inductor (represented by the letter L) and a capacitor (represented by the letter C). Both are connected in a single circuit here. An LC circuit is also known as a tank circuit, resonant circuit, or tuned circuit.
Stay tuned with Laws Of Nature for more useful interesting content.