Uncertainty In Measurement Chemistry, Class 11 NCERT

While studying chemistry, we often have to deal with experimental data and theoretical calculations. There are significant ways to be comfortable with the numbers and confidently present the data as quickly as possible. In this article, we will discuss uncertainty in measurements chemistry class 11 in detail, so let’s get started…

Uncertainty in measurement chemistry, class 11 NCERT

Inside Story

Scientific notation

Because chemistry is the study of atoms and molecules, which have tiny masses and exist in extremely large numbers, a chemist must deal with numbers of up to 602,200,000,000,000,000,000,000 molecules of 2g hydrogen gas or as small as 0.0000000000000000000000000000000166 g mass of an H atom. Similarly, other constants such as Planck’s constant, the speed of light, particle charges, etc. contain numbers in the order of magnitude mentioned above.

It might seem like fun for a moment to write or count numbers with so many zeros, but it presents a real challenge to perform simple mathematical operations like addition, subtraction, multiplication, or division of such numbers. You can enter any two numbers of the above type and try any of the operations that you want to take on as a challenge and you will really appreciate the difficulty of dealing with such numbers.

This problem is solved by using scientific notation for such numbers, that is, exponential notation, in which any number can be represented in the form of $N\times 10^n$, where $n$ is an exponent that has positive or negative values, and $N$ is a number (called the digit term) ranging from 1,000 to 9.999…. Therefore we can write 232.508 as $2.32508 \times 10^2$ in scientific notation. Note that when writing, the decimal had to be shifted two places to the left, as did the exponent (2) of 10 in scientific notation.

Likewise, 0.00016 can be written as $6\times 10^{–4}$. Here the decimal point is to be shifted four places to the right and (-4) is the exponent in scientific notation. When performing mathematical operations with numbers expressed in scientific notation, the following points should be kept in mind.

Multiplication and division

Below are two operations that follow the same rules which are there for exponential numbers, i.e.

$$ \begin{aligned} \left(5.6 \times 10^{5}\right) \times\left(6.9 \times 10^{8}\right) &=(5.6 \times 6.9)\left(10^{5+8}\right) \\ &=(5.6 \times 6.9) \times 10^{13} \\ &=38.64 \times 10^{13} \\ &=3.864 \times 10^{14} \\ \left(9.8 \times 10^{-2}\right) \times\left(2.5 \times 10^{-6}\right) &=(9.8 \times 2.5)\left(10^{-2+(-6)}\right) \\ &=(9.8 \times 2.5)\left(10^{-2-6}\right) \\ &=24.50 \times 10^{-8} \\ &=2.450 \times 10^{-7} \\ \frac{2.7 \times 10^{-3}}{5.5 \times 10^{4}}=(2.7 \div 5.5)\left(10^{-3-4}\right)=& 0.4909 \times 10^{-7} \\ =& 4.909 \times 10^{-8} \end{aligned}$$

Read Also

Addition and subtraction

For these two operations, first, the numbers are written in such a way that they have the same exponent. After that, the coefficients (digit terms) are added or subtracted as the case may be. Thus, for adding $6.65 \times 10^{4}$ and $8.95 \times 10^{3}$, the exponent is made the same for both the numbers. Thus, we get $(6.65 \times 10^4) + (0.895 × 10^4)$ Then, these numbers can be added as follows $(6.65 + 0.895) \times 10^4 = 7.545 × 10^4$ Similarly, the subtraction of two numbers can be done as shown below: \begin{aligned}(2.5 & \times 10^{–2} ) – (4.8 \times 10^{–3})\\
&= (2.5 \times 10^{–2}) – (0.48 \times 10^{–2})\\
&= (2.5 – 0.48) \times 10^{–2} \\&= 2.02 \times 10^{–2}
\end{aligned}

Significant figures

Any experimental measurement involves some uncertainty due to the limitations of the measurement instrument and the skill of the person making the measurement. For example, the mass of an object is determined using a platform scale and is 9.4g. When measuring the mass of this object on an analytical balance gives a mass of 9.4213g.

The mass determined with an analytical balance is slightly larger than the mass determined with a platform scale. Therefore, digit 4 after the decimal point in the platform scale measurement is uncertain. Uncertainties in experimental or calculated values are indicated by specifying the number of significant numbers. Significant numbers are significant digits that are known with certainty plus one that is estimated or uncertain.

The uncertainty is given by writing the definite digits and the last uncertain digit. So if we write a result as 11.2 ml, we say that 11 is true and 2 is uncertain, and the uncertainty would be $\pm 1$ in the last digit. Unless otherwise stated, an uncertainty of $\pm 1$ in the last digit is always understood.

Rules for determining significant figures

There are specific rules for determining the number of significant digits. These are listed below:

All non-zero digits are significant. For example, at 285 cm there are three significant digits and at 0.25 mL there are two significant digits.

Zeros before the first non-zero digit are not significant. This zero indicates the position of the decimal point. Therefore 0.03 has one significant digit and 0.0052 has two significant digits.
Zeros between two non-zero digits are significant. Therefore, 2.005 has four significant digits.
Zeros appear at the end or to the right of a number significant as long as they are to the right of the decimal point. For example, 200g has three significant digits. But, otherwise, trailing zeros are not significant if there is no decimal point. For example, 100 has only one significant digit, but 100. has three significant digits and 100.0 has four significant digits. Such numbers are better presented in scientific notation. We can express the number 100 as $1\times 10^2$ for one significant figure, $1.0\times 10^2$ for two significant, and $1.00\times 10^2$ for three significant figures.
Counting the number of objects, for example, 2 balls or 20 toffees, has infinite significant digits because they are exact numbers that can be represented by writing an infinite number of zeros after setting a decimal i.e., 2 = 2.000000… or 20 = 20.000000…

For numbers in scientific notation, all digits are significant, e.g $4.01 \times 10^2$ has three significant digits, and $8.256 \times 10^{-3}$ has four significant digits. However, one always wants the results to be precise and accurate, precision and precision are often mentioned when we talk about measurements.

Precision and accuracy

Precision refers to the closeness of multiple measurements for the same quantity.

Accuracy is the agreement of a given value with the true value of the result.

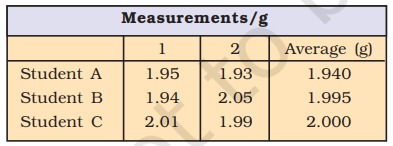
Example: The true value of a result is 2.00g and student “A” takes two measurements and reports the results as 1.95g and 1.93g.

These values are accurate as they are close, but not exact. Another student “B” repeats the experiment and gets 1.94g and 2.05g as the result of two measurements. These observations are neither precise nor exact. If the third student “C” repeats these measurements and reports 2.01g and 1.99g as the result, these values are precise and accurate.

Data to illustrate precise and accuracy

Addition and subtraction of significant figures

In addition to significant figures, the result cannot have more digits to the right of the decimal point than any of the original numbers $$\begin{array}12.11\\18.0\\1.012\\\hline{31.122}\end{array}$$ Here 18.0 has only one decimal place and the result only has to be specified up to one decimal place, i.e. 31.1

Multiplication and division of significant figures

These operations require the result to be given with no more significant digits than the measurement with fewer significant digits. 5×1.25 = 3.125, Since 2.5 has two significant digits, the result cannot have more than two significant digits therefore 3.1, Although the result is constrained to the required number of significant digits, as in the previous mathematical operation, the following points must be considered rounding Numbers.

If the rightmost digit to be omitted is more than 5, the last number is increased by one. For example 1.386. If we have to remove 6, we have to round it to 1.39.
If the rightmost digit to remove is less than that 5, the previous number does not change. For example 4.334, if 4 is to be removed then the result is rounded 4.33.
If the rightmost digit to be omitted is 5, then the last number is not changed if it is an even number but increased by one if it is an odd number. For example, if we want to round 6.35 by removing 5, we need to increase 3 to 4, which is 6.4 the result. However, if 6.25 is to be rounded, it is rounded to 6.2.

Dimensional Analysis

When calculating, it is often necessary to convert units from one system to another. The method used to do this is called the factor label method or the unit factor method or dimensional analysis. This is shown below.

Example:
A piece of metal is 3 inches (represented by in)
long. What is its length in cm?
Solution
We know that $1 in = 2.54 cm$
From this equivalence, we can write
$$\frac{1\;in}{2.54\;cm}=1=\frac{2.54\;cm}{1\;in}$$
Thus,
$\displaystyle{\frac{1\;in}{2.54\;cm}
\;\text{equals 1 and }
\frac{2.54\;cm}{1\;in}}$
also equals 1. Both of these are called unit factors. If some number is multiplied by these unit factors (i.e., 1), it will not be affected otherwise. Say, the 3 in given above is multiplied by the unit factor. So,
$\displaystyle{3\;in = 3\;in \times \frac{2.54\;cm}{1\;in}=3\times 2.54\;cm=7.62\;cm}$
Now, the unit factor by which multiplication is to be done is that unit factor $(\frac{2.54\;cm}{1\;in} \text{in the above case})$ the above case) which gives the desired units i.e., the numerator should have that part which is required in the desired result. It should also be noted in the above example that units can be handled just like other numerical parts. It can be canceled, divided, multiplied, squared, etc. Let us study one more example.

Example
A jug contains $2L$ of milk. Calculate the volume
of the milk in $m^3$.
Solution
Since $1L = 1000 \;{cm}^3$, and $1m=100\;cm$, which gives $$\frac{1\;m}{100\;cm}=1=\frac{100\;cm}{1\;m}$$ To get $m^3$ from the above unit factors, the first unit factors is taken and it is cubed. $$\left(\frac{1\;m}{100\;cm}\right)^3=\frac{1\;m^3}{10^6\;{cm}^3}=(1)^3=1$$ Now $2L=2\times 1000\;{cm}^3$. The above is multiplied by the unit factor. $$2\times 1000\;{cm}^3\times\frac{1\;m^3}{10^6\;{cm}^3}=\frac{2\;m^3}{10^3}=2\times 10^{-3}\;m^3$$

Example
How many seconds are there in 2 days?
Solution
Here, we know 1 day =24 hours (h) $$\text{or}\quad \frac{1\;\text{day}}{24\;h}=1=\frac{24\;h}{1\;\text{day}}$$ In fact, $1h=60\;\text{min}$. $$\text{or}\quad \frac{1\;h}{60\;\text{min}}=1=\frac{60\;\text{min}}{1\;h}$$ So, for converting 2days to seconds. The unit factors can be multiplied in series in one step as follows. $$2\;\text{days}\times \frac{24\;h}{1\;\text{day}}\times \frac{60\;\text{min}}{1\;h}\times \frac{60\;s}{1\;\text{min}}$$ \begin{aligned}&=2\times 24\times 60\times60\;s\\ &=172800\;s\end{aligned}

Stay tuned with Laws Of Nature for more useful and interesting content.

Was this article helpful?

YesNo