The Planck radiation law, also known as Planck’s law, describes the spectral distribution of electromagnetic radiation emitted by a black body in thermal equilibrium. It was formulated by the German physicist Max Planck in 1900 and played a pivotal role in developing quantum mechanics.
This short article will discuss the basics of Planck’s radiation law and derive its formula. So let’s get started…
Planck’s radiation law definition
Planck’s radiation law definition: It is a fundamental principle in physics that describes the spectral distribution of electromagnetic radiation emitted by a black body in thermal equilibrium, when there is no net flow of matter and energy.
Read Also:
- Black body radiation class 11: A complete guide
- Planck’s Quantum Theory class 11: A Comprehensive Guide
- Particle nature of electromagnetic radiation, class 11
- Exploring the Bohr Atomic Model: A Comprehensive Guide
Planck’s radiation law statement
Planck radiation law statement: The Planck radiation law states that the spectral radiance, or the amount of radiation emitted per unit area, per unit solid angle, and per unit wavelength, by a black body at a given temperature, is proportional to the wavelength raised to the power of minus five, multiplied by the reciprocal of the exponential function of the ratio of the wavelength and the product of the temperature and a fundamental constant called Planck’s constant (h), and the speed of light (c).
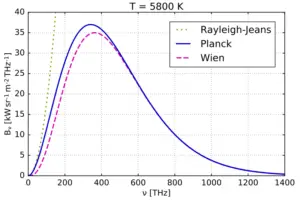
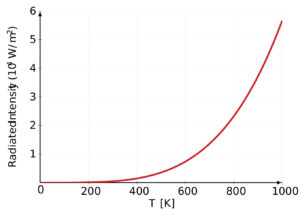
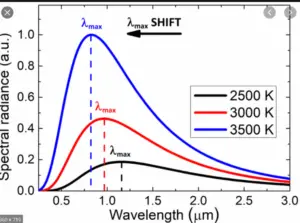
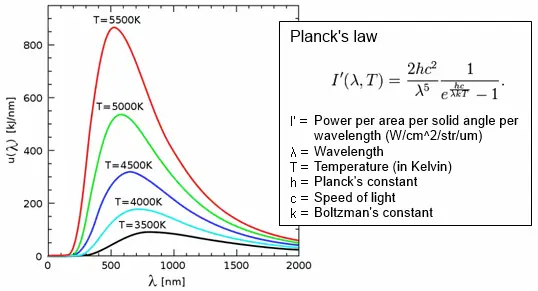
Planck’s law describes the intensity and distribution of black body radiation emitted at different wavelengths at a given temperature. It shows that as the temperature increases, the intensity of the radiation increases, and the peak of the distribution shifts to shorter wavelengths, indicating higher-energy photons. Conversely, as the temperature decreases, the intensity decreases, and the peak shifts to longer wavelengths, indicating lower-energy photons.
Planck’s radiation law introduced the concept of quantized energy levels, where energy is emitted or absorbed in discrete packets called photons. This departure from classical physics was a key step toward understanding the quantum nature of radiation and paved the way for the development of quantum mechanics. The law accurately describes the observed behavior of black body radiation and has wide-ranging applications in various fields of physics, such as astrophysics, thermodynamics, and quantum physics.
Read Also:
Planck’s radiation law formula
The mathematical expression for Planck’s radiation law is:
| $$B(\lambda, T) = \frac{2hc^2}{\lambda^5} \cdot \frac{1}{e^{\frac{hc}{\lambda kT}} – 1}$$ |
where:
B(λ, T) is the spectral radiance of the black body at a given wavelength λ and temperature T,
h is Planck’s constant (approximately $6.626 \times 10^{-34}$ Joule-seconds),
c is the speed of light (approximately $3 \times 10^8$ meters per second),
k is the Boltzmann constant (approximately $1.38 \times 10^{-23}$ Joules per Kelvin),
λ is the wavelength of the emitted radiation.
Derivation of Planck’s radiation law
The Planck radiation law describes the spectral radiance of blackbody radiation. Here are the steps to derive the formula for Planck’s radiation law:
- Assumptions:
- A blackbody is an idealized object that absorbs all incident radiation and emits radiation in thermal equilibrium.
- The energy levels in the blackbody are quantized, and the radiation is treated as composed of discrete photons.
Step 1: Consider the electromagnetic field in a cavity at thermal equilibrium. According to quantum mechanics, the energy of the field is quantized into discrete packets called photons.
Step 2: The energy of each photon is related to its frequency ((f)) or wavelength $((\lambda))$ through the equation $(E = hf)$, where (h) is Planck’s constant.
Step 3: The number of photons with a given frequency or wavelength is determined by the Bose-Einstein distribution, which describes the distribution of indistinguishable particles in quantum systems. The Bose-Einstein distribution function is given by:
$$N(\lambda) = \frac{1}{e^{\frac{hc}{\lambda k_B T}} – 1}$$
where $(k_B)$ is Boltzmann’s constant and (T) is the temperature of the black body.
Step 4: The energy density per unit volume $((u(\lambda)))$ can be obtained by summing up the energy of all the photons at a particular wavelength. Since the energy of each photon is $$(E = hf = \frac{hc}{\lambda})$$ The energy density can be expressed as:
$$u(\lambda) = \frac{8\pi hc}{\lambda^5} \cdot N(\lambda)$$
Step 5: The factor of $(8\pi)$ arises from integrating over all solid angles in three-dimensional space.
Combining all these steps, we arrive at the expression for the energy density per unit wavelength and per unit volume of black body radiation:
$$u(\lambda) = \frac{8\pi hc}{\lambda^5} \left(\frac{1}{e^{\frac{hc}{\lambda k_B T}} – 1}\right)$$
This formula represents the energy density of black body radiation as a function of wavelength $((\lambda))$.
where:
- (h) is Planck’s constant,
- (c) is the speed of light,
- $(\lambda)$ is the wavelength,
- (k_B) is Boltzmann’s constant, and
- (T) is the temperature of the black body.
Step 6: To obtain the spectral radiance $(B(\lambda))$, we need to consider the energy emitted per unit area, per unit solid angle, and per unit wavelength. The spectral radiance is given by:
$$B(\lambda) = \frac{c}{4\pi} \cdot u(\lambda)$$
Step 7: Substitute the expression for $(u(\lambda))$ into the equation for $(B(\lambda))$ to obtain:
$$B(\lambda) = \frac{2hc^2}{\lambda^5} \left(\frac{1}{e^{\frac{hc}{\lambda k_B T}} – 1}\right)$$
This is the Planck radiation law in terms of wavelength $((\lambda))$.
Please note that (h), (c), $(k_B)$, and (T) are constants, and $(\lambda)$ is the variable representing the wavelength.
Read Also:
- Rutherford atomic model: postulates, observations, and limitations, class 11
- Thomson model of atom: postulates, drawbacks, & significance, class 11
- Cathode Tube Ray Experiment class 11: working, procedure, observation, and conclusion
- Discovery of Electron class 11: chemistry, NCERT
- Discovery of proton class 11: chemistry NCERT
- Wave nature of electromagnetic radiation, class 11
Frequently Asked Questions (FAQs)
What is Planck’s radiation law?
Planck’s radiation law is a fundamental principle in quantum mechanics and thermodynamics that describes the spectral distribution of radiation emitted by a blackbody at a given temperature. It provides a formula for the intensity of radiation at different wavelengths or frequencies.
Who formulated Planck’s radiation law, and when was it developed?
Planck’s radiation law was formulated by the German physicist Max Planck in 1900. It marked a groundbreaking development in understanding the behavior of electromagnetic radiation and laid the foundation for quantum mechanics.
How does Planck’s radiation law relate to the concept of quantization?
Planck introduced the idea of quantization in the context of radiation. He proposed that energy is emitted or absorbed in discrete units, called quanta, which are proportional to the frequency of the radiation. This concept of quantization was a crucial step toward the development of quantum mechanics.
What is the significance of Planck’s radiation law in modern physics?
Planck’s radiation law played a pivotal role in the development of quantum mechanics, which revolutionized our understanding of the behavior of matter and energy at the atomic and subatomic levels. It is considered one of the cornerstones of modern physics and has applications in fields such as astrophysics and quantum theory.
How is Planck’s radiation law expressed mathematically?
The mathematical expression for Planck’s radiation law is:
$$B(\lambda, T) = \frac{2hc^2}{\lambda^5} \cdot \frac{1}{e^{\frac{hc}{\lambda kT}} – 1}$$
This formula describes how the intensity of blackbody radiation changes with temperature and wavelength, providing insights into the distribution of energy across different parts of the electromagnetic spectrum.
Stay tuned with Laws Of Nature for more useful and interesting content.