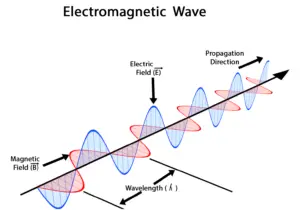
Displacement current is an electromagnetism concept first proposed by James Clerk Maxwell in the mid-nineteenth century. It is a critical component of Maxwell’s equations, which provide a comprehensive description of the behavior of electric and magnetic fields, as well as electromagnetic phenomena.
Displacement current is produced by the movement of electric charges in a changing electric field and is used to explain the behavior of electromagnetic waves such as light and radio waves. The displacement current concept has important practical applications in modern electrical technology, such as wireless communication, radar, and imaging technology. In this article, we will look at displacement current, its definition, formula, ampere’s law modification, and properties. So let’s get started…
History of displacement current
In the mid-nineteenth century, James Clerk Maxwell introduced the concept of displacement current as part of his formulation of electromagnetism. Maxwell’s work built on previous discoveries in the fields of electricity and magnetism, including those of Michael Faraday and André-Marie Ampère.

Faraday discovered electromagnetic induction in 1831, which is the idea that a changing magnetic field can cause an electric current to flow through a conductor. Faraday’s discovery paved the way for the development of generators and motors, both of which are vital components of modern electrical technology.
Ampère, on the other hand, invented the concept of circulating currents and devised Ampere’s circuital law, which relates the magnetic field around a closed loop to the current flowing through that loop.
Maxwell combined these earlier discoveries and developed a set of equations known as Maxwell’s equations in the 1860s. These equations describe the behavior of electric and magnetic fields and thoroughly explain electromagnetic phenomena.
The Ampere-Maxwell equation, one of Maxwell’s equations, relates the curl of the magnetic field to the electric current and the electric field’s time rate of change. This equation, however, did not account for all observed electromagnetic phenomena.
Maxwell realized that the Ampere-Maxwell equation needed a new term to account for the displacement of electric charges caused by a changing electric field. To explain this phenomenon, he proposed the concept of displacement current.
Maxwell’s displacement current formulation assisted in explaining the behavior of electromagnetic waves, which are disturbances that propagate through space as a combination of electric and magnetic fields. It also paved the way for radio communication and other forms of wireless technology to emerge.
What is Ampere’s circuital law?
Ampere’s circuital law is a fundamental law of electromagnetism that relates the magnetic field surrounding a closed loop to the current flowing through it.
Ampere’s circuital law: The line integral of the magnetic field around a closed loop is proportional to the current passing through the loop, according to the law. The law is expressed mathematically as:
$$\oint B\cdot dl=\mu_0 I$$
where $B$ denotes the magnetic field, $dl$ denotes an infinitesimal length loop element, $I$ denotes the current flowing through the loop, and $\mu_0$ denotes the permeability of free space.
Ampere’s circuital law is one of four of Maxwell’s equations that describe the behavior of electric and magnetic fields and provide a complete description of electromagnetic phenomena.
The law is critical for understanding the behavior of magnetic fields around current-carrying conductors such as electromagnets and electric motors. It also has important practical applications in electrical and electronic technology, such as power generation and distribution, electric motors, and transformers.
Inconsistency in Ampere’s circuital law
Ampere’s circuital law is one of the fundamental laws of electromagnetism, which relates the magnetic field around a closed loop to the current passing through that loop. According to the law, the line integral of the magnetic field around a closed loop is proportional to the current enclosed by that loop.
However, there is an inconsistency in Ampere’s circuital law when it comes to parallel plate capacitors. A parallel plate capacitor consists of two parallel plates separated by a distance $d$, with a potential difference $V$ applied between the plates. When a current flows through a wire connected to the plates, it charges the plates and sets up an electric field between them.
According to Ampere’s circuital law, the magnetic field around a closed loop should be proportional to the current enclosed by that loop. However, in the case of a parallel plate capacitor, the current passing through the plates is zero, since the charges on the plates are stationary. Therefore, there should be no magnetic field around the capacitor.
But we know from experiments that a magnetic field is indeed present around a parallel plate capacitor when a current is flowing through the wire connected to the plates. This magnetic field is caused by the displacement current, which is a term introduced by James Clerk Maxwell to account for the changing electric field between the plates.
The displacement current is proportional to the rate of change of the electric flux and is given by the equation:
$$I_d = \varepsilon_0 \frac{d\phi_E}{dt}$$
where $I_d$ is the displacement current, $\varepsilon_0$ is the permittivity of free space, and $\phi_E$ is the electric flux between the plates.
However, the displacement current does not satisfy the continuity equation, which states that the divergence of the current density must be zero, i.e., $\displaystyle \nabla \cdot J = 0$. This is because the displacement current is not an actual conduction current, and it does not involve the motion of charges.
So the inconsistency in Ampere’s circuital law with parallel plate capacitors is due to the displacement current, which must be included in the modified form of the law.
What is the conduction current?
Conduction current definition: Conduction current refers to the flow of electric charges through a conducting material such as a wire, due to the motion of free electrons in response to an applied electric field. This is the current that is commonly associated with the flow of electricity in everyday electrical circuits.
Mathematically, conduction current is simply given by Ohm’s law as follows: $$I_C =\frac{V}{R}$$
Where:
$I_C$ is conduction current, $V$ is the potential difference between the battery terminal, and $R$ is the resistance of the circuit.
Read Also:
- Transformer – Definition, Types, Working Principle, and Constructions
- LC oscillation class 12
- Expression for energy and average power stored in a pure capacitor
- Electromagnetic waves: definition, equation, graphical representation, and applications
What is displacement current?
Displacement current definition: Displacement current is a type of current introduced by James Clerk Maxwell to account for the changing electric field in regions where there is no conduction current. It arises due to the displacement of charges in a dielectric material such as air or insulators, in response to a time-varying electric field.
What is the need for displacement current class 12?
In electromagnetism, a changing electric field produces a magnetic field, and a changing magnetic field produces an electric field. These two phenomena are described by Faraday’s law and Ampere’s law, respectively. However, there is a third phenomenon that occurs in the presence of a changing electric field, which is known as displacement current.
The need for displacement current arises due to the fact that a changing electric field creates a magnetic field, even if there is no actual flow of charge. This is because a changing electric field induces a changing electric flux in the space around it, which in turn generates a changing magnetic field. This changing magnetic field can then affect the behavior of nearby electric circuits.
To understand how displacement current works in a circuit, consider a simple circuit consisting of a capacitor and a resistor. When a voltage is applied to the capacitor, charge accumulates on its plates, and an electric field is created between them. As the electric field changes over time, a magnetic field is generated, which can induce a current in the nearby resistor.
This current is not due to the flow of charge across the capacitor plates, but rather due to the changing electric field in the capacitor, which creates a displacement current that induces a magnetic field that affects the nearby circuit.
The concept of displacement current is important in the study of electromagnetism, as it helps to explain many phenomena related to the behavior of electric and magnetic fields. For example, it is crucial in the understanding of electromagnetic waves, which are a combination of electric and magnetic fields that propagate through space.
Displacement current formula, class 12
Displacement current formula: The displacement current is proportional to the rate of change of the electric flux and is given by the equation:
$$I_d = \varepsilon_0 \frac{d\phi_E}{dt}$$
where $I_d$ is the displacement current, $\varepsilon_0$ is the permittivity of free space, and $\phi_E$ is the electric flux between the plates.
Displacement current derivation class 12
To derive the formula for displacement current, we start with Maxwell’s equations in their integral form:
| $$\oint \vec{E}\cdot d\vec{A} = \frac{Q}{\epsilon_0}, \quad\quad \oint \vec{B}\cdot d\vec{l} = \mu_0 I + \mu_0\epsilon_0 \frac{d}{dt}\iint \vec{E}\cdot d\vec{A}$$ |
where $\vec{E}$ is the electric field, $\vec{B}$ is the magnetic field, $Q$ is the charge enclosed by the surface, $I$ is the current flowing through the wire, $\epsilon_0$ is the permittivity of free space, and $\mu_0$ is the permeability of free space.
The second equation is known as Ampere’s law with the Maxwell’s correction term, which includes the contribution of the time-varying electric field $\vec{E}$ in the form of the term: $$\mu_0\epsilon_0 \frac{d}{dt}\iint \vec{E}\cdot d\vec{A}$$
Let’s consider a capacitor with plates of area $A$ and separation $d$. When a time-varying voltage $V(t)$ is applied across the plates, an electric field $\vec{E}$ is established between the plates. The electric field is given by:
$$E = \frac{V(t)}{d}$$
The time-varying electric field between the plates of the capacitor produces a displacement current $I_d$ given by:
$$I_d = \epsilon_0\frac{d}{dt}\iint \vec{E}\cdot d\vec{A}$$
Substituting the expression for the electric field, we get:
| $$I_d = \epsilon_0\frac{d}{dt}\iint \frac{V(t)}{d} dA = \epsilon_0 A \frac{d}{dt} \left(\frac{V(t)}{d}\right) = \frac{\epsilon_0 A}{d}\frac{dV}{dt}$$ |
Therefore, the formula for the displacement current is:
$$\boxed{I_d = \epsilon_0 \frac{d\Phi_E}{dt}}$$
where $\Phi_E$ is the electric flux through a surface, given by:
$$\Phi_E = \iint \vec{E}\cdot d\vec{A}$$
This formula expresses the relationship between the time-varying electric field and the displacement current, and it is a fundamental equation in electromagnetism.
Difference between conduction and displacement current
The key difference between conduction current and displacement current is that conduction current involves the flow of electric charges through a conducting material, while displacement current does not involve the flow of charges. Instead, displacement current arises due to the changing electric field and the resulting displacement of charges in a dielectric material.
In mathematical terms, the conduction current density $J_c$ is related to the electric field $E$ and the conductivity $\sigma$ of the material by the equation:
$$J_c = \sigma E$$
whereas the displacement current density $J_d$ is related to the rate of change of the electric field $E$ and the permittivity $\varepsilon$ of the material by the equation:
$$J_d = \varepsilon \frac{dE}{dt}$$
In a vacuum or air, $\varepsilon$ is approximately equal to the permittivity of free space, $\varepsilon_0$.
So, conduction current is the flow of electric charges through a conducting material, while displacement current is a term that accounts for the changing electric field in regions where there is no conduction current, and arises due to the displacement of charges in a dielectric material.
Maxwell’s modification of Ampere’s circuital Law
Ampere’s circuital law relates the magnetic field around a closed loop to the current passing through that loop. According to Ampere’s law, the line integral of the magnetic field around a closed loop is proportional to the current enclosed by that loop.
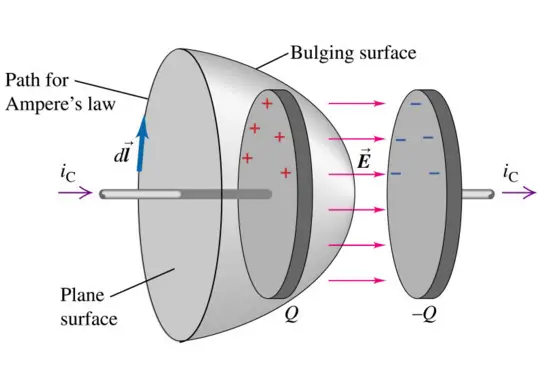
However, James Clerk Maxwell discovered an inconsistency in Ampere’s circuital law when he developed his electromagnetic theory in the 1860s. Maxwell discovered that the law did not hold true in situations where there was a time-varying electric field, such as in a changing magnetic field or in a capacitor with a changing electric field.
To account for this inconsistency, Maxwell used symmetry to modify Ampere’s law. According to Faraday’s law, a changing magnetic field induces an electric field, so a changing electric field must induce a magnetic field. Because currents are the most common sources of magnetic fields, a changing electric field must be associated with a current. To distinguish it from the usual conduction current caused by electron drift, Maxwell named this current the displacement current.
Displacement current is the current that exists in addition to the conduction current whenever the electric field and thus the electric flux change over time.
To maintain dimensional consistency, the displacement current is given the form:
$$I_d = \varepsilon_0 \frac{d\phi_E}{dt}$$
Therefore, the total current across the closed loop is given as
$$I_c + I_d = I_c + \varepsilon_0 \frac{d\phi_E}{dt}$$
Hence, the modified form of Ampere’s circuital law, also known as the Ampere-Maxwell law, is:
$$\oint B\cdot dl=\mu_0 \left(I + \varepsilon_0 \frac{d\phi_E}{dt}\right)$$
where $B$ is the magnetic field, $dl$ is an element of length along the closed loop, $\mu_0$ is the permeability of free space, $I$ is the conduction current passing through the loop, $\varepsilon_0$ is the permittivity of free space, and $\displaystyle\frac{d\phi_E}{dt}$ is the rate of change of electric flux through the surface enclosed by the loop.
The additional term, $\displaystyle\varepsilon_0 \frac{d\phi_E}{dt}$, is the displacement current and accounts for the changing electric field. This term allows for the full consistency between Ampere’s law and the other laws of electromagnetism, including Faraday’s law of electromagnetic induction and Gauss’s law for electric fields.
The modified form of Ampere’s law, along with the other three Maxwell’s equations, formed the foundation of classical electrodynamics, which has been successful in explaining a wide range of electromagnetic phenomena.
Consistency of modified Ampere’s circuital law
Let’s consider a parallel plate capacitor with plates of area $A$, separated by a distance $d$, and charged with a charge $Q$. When a battery is connected to the capacitor, it creates a uniform electric field $E$ between the plates, given by:
$$E = \frac{Q}{ \varepsilon_0 A}$$
where $\varepsilon_0$ is the permittivity of free space.
When the capacitor is fully charged, there is no conduction current flowing through it, as there are no moving charges. However, there is a changing electric field between the plates, and hence a displacement current flows through the capacitor.
To show the consistency of the modified Ampere’s circuital law for the parallel plate capacitor, we can apply the law to a closed loop around the edge of one of the plates.
Using the right-hand rule, we can see that the magnetic field around the loop is in the same direction as the current flowing through the loop. Since there is no conduction current flowing through the capacitor, the only current passing through the loop is the displacement current, given by:
$$I_d = \varepsilon_0 A \frac{dE}{dt}$$
Substituting this expression into the modified Ampere’s circuital law, we get:
$$\oint B \cdot dl = \mu_0(I_d)$$
Since the loop is around the edge of one of the plates, the magnetic field is zero everywhere along the loop. Hence, the line integral of the magnetic field around the loop is zero, and we are left with:
$$0 = \mu_0(I_d)$$
Substituting the expression for the displacement current, we get:
$$0 = \mu_0\left(\varepsilon_0 A \frac{dE}{dt}\right)$$
Simplifying this expression using the relationship between the electric field and the charge on the capacitor, we get:
$$0 = \frac{dQ}{dt}$$
which is just a statement of the conservation of charge.
Therefore, we see that the modified Ampere’s circuital law is consistent with the behavior of a parallel plate capacitor. It correctly accounts for the displacement current that flows through the capacitor when there is a changing electric field, and it reduces to the original Ampere’s law in situations where there is only conduction current.
Read Also
- Sharpness of Resonance: Q-Factor in LCR circuit, class 12
- Power in an AC circuit: definition, and formula derivation
- Choke coil – principle, working, and construction, class 12
- Resonance condition in a series LCR circuit
- Wattless current class 12
- Expression for energy and average power stored in an inductor
Property of continuity
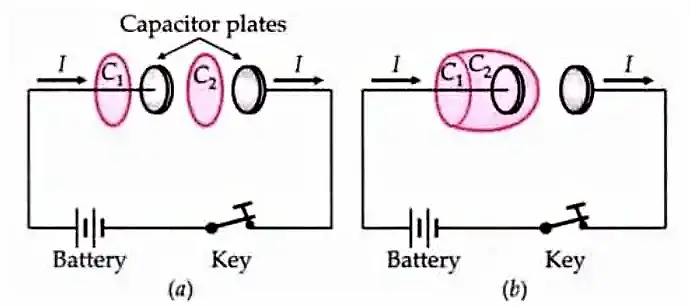
Property of continuity. The sum $\left(I_c+I_d\right)$ has the important property of continuity along any closed path even when individually $I_c$ and $I_d$ may not be continuous. In Fig above, for example, a current $I_c$ enters one plate and leaves the other plate of the capacitor. The conduction current $$ I_=\frac {d q}{d t}$$ is not continuous across the capacitor gap as no charge is transported across this gap. The displacement current $I_d$ is zero outside the capacitor plates and in the gap, it has the value
$$\varepsilon_0 \frac{d \phi_E}{d t}=\varepsilon_0 \frac{d}{d t}(E A)=\varepsilon_0 \frac{d}{d t}\left(\frac{q}{\varepsilon_0}\right)=\frac{d q}{d t} $$
which is exactly the value of the conduction current in the lead wires. Thus the displacement current satisfies the basic condition that the current is continuous.
The sum $I_c+\varepsilon_0 \frac{d \phi_E}{d t}$ has the same value along the entire path (both inside and outside the capacitor plates), although individually the two currents are discontinuous.
Clearly, outside the capacitor plates, we have only conduction current $I_c=I$, and there is no displacement current $\left(I_d=0\right)$. While inside the capacitor plates, there is only displacement current $I_d=I$, and there is no conduction current $\left(I_c=0\right)$. But in any general medium, both $I_c$ and $I_d$ are present. However, $I_c$ is larger than $I_d$ in a conducting medium while $I_d$ is larger than $I_c$ in an insulating medium.
Consequences of displacement current class 12
The consequences of displacement current are significant in the study of electromagnetism, as it helps to explain a number of electromagnetic phenomena. Here are some of the major consequences of displacement current:
- Explanation of the behavior of capacitors: Displacement current is the current that flows through a capacitor when it is being charged or discharged. This current is necessary to maintain the continuity equation, and it produces a magnetic field around the capacitor that can affect nearby circuits.
- Modification of Ampere’s circuital law: The discovery of displacement current led to the modification of Ampere’s circuital law, which is now known as the Ampere-Maxwell law. This modification made the law consistent with the other laws of electromagnetism, including Faraday’s law of electromagnetic induction and Gauss’s law for electric fields.
- Prediction of electromagnetic waves: The presence of displacement current in Maxwell’s equations led him to predict the existence of electromagnetic waves, which are oscillating electric and magnetic fields that can propagate through space at the speed of light. This prediction was later confirmed experimentally by Heinrich Hertz, and it formed the basis of the modern theory of electromagnetic radiation.
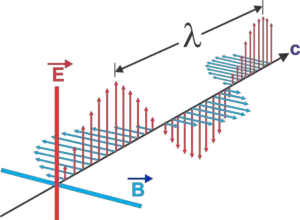
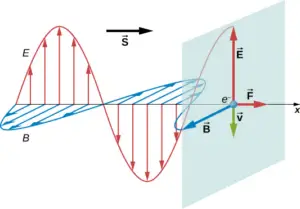
- Involved in the propagation of electromagnetic waves: Electromagnetic waves are generated by the acceleration of charged particles, which creates both electric and magnetic fields. The changing electric field produces a displacement current, which in turn produces a magnetic field. The resulting oscillating electric and magnetic fields travel together as electromagnetic waves.
- Development of modern technology: The discovery of displacement current and the subsequent development of electromagnetic theory paved the way for the development of many modern technologies, including radio and television broadcasting, radar, microwave communication, and many medical imaging techniques.
Properties of displacement current class 12
Displacement current is a fundamental concept in electromagnetism that describes the flow of electric charge in a region of space where there is a changing electric field. Here are some of the important properties of displacement current are:
- It is proportional to the rate of change of the electric field: Displacement current is given by the equation $\displaystyle I_d = \varepsilon_0 \frac{d\phi_E}{dt}$, where $I_d$ is the displacement current, $\varepsilon_0$ is the permittivity of free space, $\phi_E$ is the electric flux through a surface, and $dt$ is a small time interval. This equation shows that the magnitude of displacement current is directly proportional to the rate of change of the electric field.
- It is not a real current: Unlike conduction current, which is the movement of charged particles through a conductor, displacement current is a virtual current that arises due to a changing electric field. There are no actual moving charges involved in displacement current.
- It produces a magnetic field: Like conduction current, displacement current produces a magnetic field. When displacement current flows through a region of space, it produces a magnetic field that can interact with other nearby magnetic fields.
- It satisfies the continuity equation: Displacement current is an essential part of the continuity equation, which states that the net flow of electric charge into or out of any closed surface must be equal to the rate of change of charge within the surface. In situations where there is a changing electric field, the continuity equation requires the inclusion of displacement current to maintain its validity.
- It plays a role in the propagation of electromagnetic waves: Electromagnetic waves are generated by the acceleration of charged particles, which creates both electric and magnetic fields. The changing electric field produces a displacement current, which in turn produces a magnetic field. The resulting oscillating electric and magnetic fields travel together as electromagnetic waves.
Significance of displacement current class 12
The following points describes the significance of displacement current:
- It explains how electromagnetic waves behave: Displacement current is an important factor in the generation of electromagnetic waves. It would be impossible to explain electromagnetic wave propagation through space without displacement current.
- It explains how capacitors work: capacitors store electrical charge, and charging and discharging a capacitor involves the flow of displacement current.
- Displacement current is important in the design of electronic circuits: Displacement current is important in the design and operation of electronic circuits, particularly those involving high-frequency signals.
- It is a fundamental concept in electromagnetism: Along with electric fields, magnetic fields, and electric charges, displacement current is one of the four fundamental concepts in electromagnetism.
- It is linked to charge conservation: Displacement current is linked to charge conservation, which is a fundamental principle in physics. Understanding displacement current allows us to better understand charge conservation in electric and magnetic fields.
The concept of displacement current is important in electromagnetism because it has important implications for our understanding of how electric and magnetic fields interact with each other and with matter.
Solved Numericals on displacement current
| Example 1. The voltage between the plates of $a$ parallel-plate capacitor of capacitance $1.0 \mu \mathrm{F}$ is changing at the rate of $5 \mathrm{Vs}^{-1}$. What is the displacement current in the capacitor? Solution: Here $C=1.0 \mu \mathrm{F}=1.0 \times 10^{-6} \mathrm{~F}$, $$ \frac{d V}{d t}=5 \mathrm{Vs}^{-1} $$ Displacement current, $$ \begin{aligned} I_D & =\varepsilon_0 \frac{d \phi_E}{d t}=\varepsilon_0 \frac{d}{d t}(E A)=\varepsilon_0 \frac{d}{d t}\left(\frac{V A}{d}\right) \\ & =\frac{\varepsilon_0 A}{d} \frac{d V}{d t}=C \frac{d V}{d t} \\ & =1.0 \times 10^{-6} \times 5 \mathrm{~A}=5.0 \mu \mathrm{A} . \end{aligned} $$ Example 2. A parallel plate capacitor has circular plates, each of radius $5.0 \mathrm{~cm}$. It is being charged so that electric field in the gap between its plates rises steadily at the rate of $10^{12} \mathrm{Vm}^{-1} \mathrm{~s}^{-1}$. What is the displacement current? Solution: Here $r=5 \mathrm{~cm}=5 \times 10^{-2} \mathrm{~m}$, $$ \frac{d E}{d t}=10^{12} \mathrm{Vm}^{-1} \mathrm{~s}^{-1} $$ Displacement current, $$ \begin{aligned} I_D & =\varepsilon_0 \frac{d \phi_E}{d t}=\varepsilon_0 A \frac{d E}{d t}=\varepsilon_0 \cdot \pi r^2 \frac{d E}{d t} \\ & =8.85 \times 10^{-12} \times \pi \times\left(5 \times 10^{-2}\right) \times 10^{12} \mathrm{~A}=0.07 \mathrm{~A} . \end{aligned} $$ Example 3. A parallel plate capacitor has two metal plates of size $30 \mathrm{~cm} \times 15 \mathrm{~cm}$ and is separated by $2.0 \mathrm{~mm}$. The capacitor is being charged so that the charging current has a steady value of $100 \mathrm{~mA}$. Calculate the rate of change of the potential difference between the capacitor plates. What is the displacement current in the region between the capacitor plates? Solution: $$ \begin{aligned} I&=\frac{d q}{d t} =\frac{d}{d t}(C V)\\&=C \frac{d V}{d t}=\frac{\varepsilon_0 A}{d} \cdot \frac{d V}{d t} \\ \therefore \frac{d V}{d t} & =\frac{I d}{\varepsilon_0 A} \\ & =\frac{100 \times 10^{-3} \times 2 \times 10^{-3}}{8.85 \times 10^{-12} \times 0.30 \times 0.15}\\&=5\times 10^8 Vs^{-1} \end{aligned} $$ Displacement current is the same as conduction current i.e $\displaystyle I_c = I_d = 100mA$ |
Frequently Asked Questions – FAQs
What is displacement current and its formula?
Displacement current is a type of electric current that arises due to a changing electric field. It was first proposed by James Clerk Maxwell as a term in his famous set of equations known as Maxwell’s equations.
Displacement current is important in understanding the behavior of electromagnetic waves, and it plays a crucial role in the operation of many electrical devices, such as capacitors and transformers.
The formula for displacement current is:
$$I_d = \varepsilon_0 \frac{d\phi_E}{dt}$$
where $I_d$ is the displacement current, $\varepsilon_0$ is the permittivity of free space, and $\frac{d\phi_E}{dt}$ is the rate of change of the electric flux density in a region of space. The electric flux density is a measure of the strength of the electric field in a given area.
What is the unit of displacement current?
The SI unit of displacement current is Ampere (A).
State Ampere-Maxwell law.
Ampere-Maxwell law states that the line integral of the magnetic field around a closed loop is equal to μ0 times the sum of the conduction current and displacement current.
Distinguish between conduction current and displacement current?
The flow of electrons in a circuit causes a conduction current. It exists even when electrons flow at a constant rate. The time-varying electric field causes displacement current. Under steady conduction, it does not exist.
What current exists inside a capacitor?
The current that exists inside the capacitor is the Displacement current.
Stay tuned with Laws Of Nature for more useful and interesting content.