The study of electromagnetic waves has revolutionized our understanding of the physical world and has transformed the way we communicate, generate energy and explore the universe. These waves are all around us, from the radio waves that bring music to our ears, to the light that illuminates our world, to the X-rays that allow us to peer inside the human body.
But beyond their ubiquitous presence, electromagnetic waves also possess a fascinating set of properties that can be measured and analyzed. In this article, we will delve into three of the most important characteristics of electromagnetic waves: intensity, momentum, and radiation pressure. We will explore what these properties are, how they are related to each other, and how they impact the behavior of electromagnetic waves in different contexts.
By the end of this article, you’ll have a deeper understanding of the fundamental principles that underlie one of the most important phenomena in the physical world.
What are electromagnetic waves?
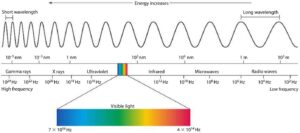
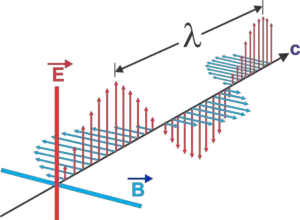
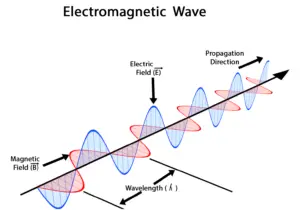
Electromagnetic waves are a type of wave that consists of oscillating electric and magnetic fields that travel through space at the speed of light. They are generated by the motion of charged particles and can range from low-frequency radio waves to high-frequency gamma rays.
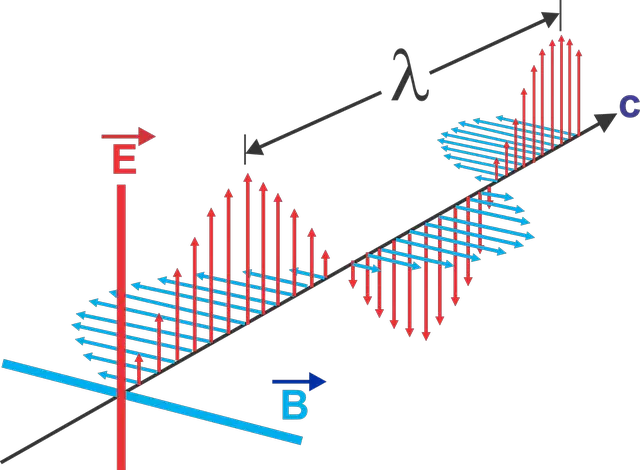
Electromagnetic waves are characterized by their wavelength and frequency, which determine their energy and the type of electromagnetic radiation they produce. They do not require a medium to travel through and can propagate through a vacuum.
Read Also:
Intensity of an electromagnetic wave, class 12
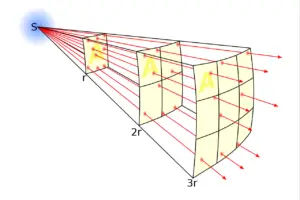
The intensity of an electromagnetic wave is a measure of the rate at which energy is transported by the wave per unit area perpendicular to the direction of wave propagation. Mathematically, it is defined as the power per unit area and is given by the formula:
\begin{equation} \text{Intensity} = \frac{\text{Power}}{\text{Area}} \end{equation}
The unit of intensity is watts per square meter (W/m²). As an electromagnetic wave travels through space, its intensity decreases with distance from the source, because the same amount of energy is spread out over a larger area. The intensity of an electromagnetic wave can be measured using a device called a radiometer or by detecting the force exerted by the wave on a charged particle.
The intensity of an electromagnetic wave is proportional to the square of its electric field amplitude, which means that doubling the electric field amplitude results in a fourfold increase in intensity. Intensity is an important parameter in many applications of electromagnetic waves, including communication, energy transmission, and medical imaging.
Derive the formula for the Intensity of electromagnetic wave
The intensity of an electromagnetic wave is the rate at which energy is transported by the wave per unit area perpendicular to the direction of wave propagation. To derive the formula for intensity, we can start with the formula for the energy density of an electromagnetic wave.
The energy density (u) of an electromagnetic wave is given by:
\begin{equation} u = \frac{1}{2}\epsilon_0E^2 + \frac{1}{2\mu_0}B^2 \end{equation}
where E is the electric field strength, B is the magnetic field strength, ε0 is the electric constant (permittivity of free space), and μ0 is the magnetic constant (permeability of free space).
The instantaneous power (P) carried by an electromagnetic wave is given by:
\begin{equation} P = uAc \end{equation}
where A is the cross-sectional area of the wave and c is the speed of light.
The intensity (I) of the wave is defined as the power per unit area:
\begin{equation} I = \frac{P}{A} = \frac{uAc}{A} = uc \end{equation}
Substituting the expression for u from equation (1), we get:
\begin{equation} I = \frac{\epsilon_0}{2}E^2c + \frac{1}{2\mu_0}B^2c \end{equation}
Thus, the formula for the intensity of an electromagnetic wave is:
\begin{equation} I = \frac{1}{2}\epsilon_0E^2c + \frac{1}{2\mu_0}B^2c \end{equation}
where E and B are the electric and magnetic field strengths of the wave, respectively, and ε0 and μ0 are the electric and magnetic constants of free space, respectively.
Read Also:
- Energy density of electromagnetic wave, class 12
- Nature of electromagnetic waves, class 12
- Hertz’s experiment electromagnetic waves, class 12
Momentum of electromagnetic waves, class 12
Electromagnetic waves have momentum, which is a consequence of their energy and momentum transport properties. The momentum p of an electromagnetic wave is given by:
\begin{equation} p = \frac{E}{c} \end{equation}
where $E$ is the energy of the wave and $c$ is the speed of light.
This expression can be derived from the de Broglie relation, which relates the momentum of a particle to its wavelength. For an electromagnetic wave, the wavelength $\lambda$ is related to the frequency $f$ by the formula $\displaystyle \lambda = \frac{c}{f}$, where $c$ is the speed of light. The energy $E$ of a wave is related to its frequency by the formula $\displaystyle E = hf$, where $h$ is Planck’s constant. Substituting $\displaystyle \lambda = \frac{c}{f}$ and $\displaystyle E = hf$ into the de Broglie relation, we get:
\begin{equation} p = \frac{h}{\lambda} = \frac{hf}{c} = \frac{E}{c} \end{equation}
This expression shows that the momentum of an electromagnetic wave is proportional to its energy and inversely proportional to the speed of light. Since electromagnetic waves can travel through a vacuum, they can transfer momentum even in the absence of a physical medium. This property is important in a variety of applications, such as solar sails, where the momentum of sunlight is used to propel spacecraft.
Radiation pressure of electromagnetic waves, class 12
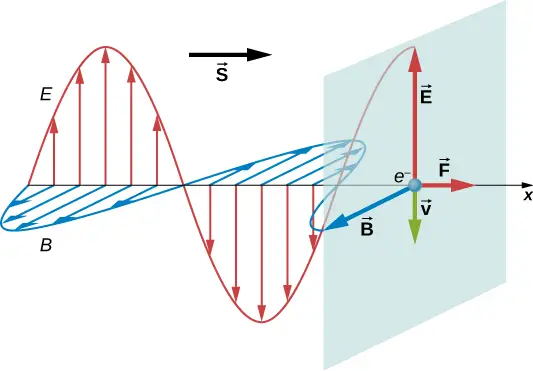
Electromagnetic waves also exert pressure on objects they interact with, known as radiation pressure. This pressure arises from the transfer of momentum from the wave to the object, and is given by:
\begin{equation} P = \frac{I}{c} \end{equation}
where $P$ is the pressure, $I$ is the intensity of the wave, and $c$ is the speed of light.
This formula can be derived from the momentum formula for an electromagnetic wave, $\displaystyle p = \frac{E}{c}$, by considering a plane wave incident on a perfectly reflecting surface. The reflection of the wave results in a change in momentum, and the corresponding change in momentum per unit of time gives rise to pressure. The pressure is found to be proportional to the intensity of the wave, and inversely proportional to the speed of light.
Radiation pressure has a variety of important applications, such as in solar sails, where the pressure exerted by sunlight is used to propel spacecraft, and in laser cooling, where the pressure exerted by laser light is used to slow down and trap atoms.
Read Also:
- Transformer – Definition, Types, Working Principle, and Constructions
- LC oscillation class 12
- Expression for energy and average power stored in a pure capacitor
- Sources of electromagnetic waves, class 12
- Mathematical representation of electromagnetic waves, class 12
- Maxwell’s prediction of electromagnetic waves, class 12
Frequently Asked Questions – FAQs
What is the formula for the intensity of electromagnetic waves?
The intensity of an electromagnetic wave is a measure of the rate at which energy is transported by the wave per unit area perpendicular to the direction of wave propagation. Mathematically, it is defined as the power per unit area and is given by the formula:
\begin{equation} \text{Intensity} = \frac{\text{Power}}{\text{Area}} \end{equation}
What is the intensity of a wave?
The intensity of an electromagnetic wave is the rate at which energy is transported by the wave per unit area perpendicular to the direction of wave propagation
What is the formula for momentum in electromagnetic waves?
Electromagnetic waves have momentum, which is a consequence of their energy and momentum transport properties. The momentum p of an electromagnetic wave is given by:
\begin{equation} p = \frac{E}{c} \end{equation}
where $E$ is the energy of the wave and $c$ is the speed of light.
What is the momentum of an EM wave in terms of wavelength?
The momentum p of an electromagnetic wave in terms of wavelength $\lambda$ is given by: \begin{equation} p = \frac{E}{\lambda f} \end{equation}
where $E$ is the energy of the wave, $\lambda$ is the wavelength of the wave, and $f$ is the frequency of the wave.
Why do electromagnetic waves exert radiation pressure?
Electromagnetic waves exert radiation pressure because they carry both energy and momentum and when they interact with matter, they transfer some of this energy and momentum to the object.
This transfer of momentum results in a force exerted on the object, which we experience as radiation pressure. The pressure is proportional to the intensity of the wave and inversely proportional to the speed of light.
What is the radiation pressure formula?
Electromagnetic waves also exert pressure on objects they interact with, known as radiation pressure. This pressure arises from the transfer of momentum from the wave to the object, and is given by:
\begin{equation} P = \frac{I}{c} \end{equation}
where $P$ is the pressure, $I$ is the intensity of the wave, and $c$ is the speed of light.
Stay tuned with Laws Of Nature for more useful and interesting content.