In this article we are going to derive an expression for magnetic field on the axis of circular current carrying loop. So without talking so much let’s gets started…

MAGNETIC FIELD ON THE AXIS OF A CIRCULAR CURRENT CARRYING LOOP

AT ANY POINT ON THE AXIS

Let’s consider a circular loop of radius a with centre C.[latexpage] Let the plane of the coil be perpendicular to the plane of the paper and current $I$ be flowing in the direction shown.

Suppose, P is the any point on the axis at direction r from the centre. See figure below.

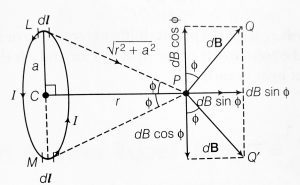
Now consider a current element $\displaystyle{Idl}$ on the top (L) where current comes out of the paper normally whereas at the bottom (M) enters into the plane of the paper normally.
$$\text{therefore},\qquad LP\perp dl$$
$$\text{also}\qquad MP\perp dl$$
$$\therefore \qquad LP=MP=\sqrt{r^2+a^2}$$
According to the Biot-Savart Law, magnetic field due to current element $\displaystyle{Idl}$ at the point P is given as-
$$dB=\frac{\mu_0 \mu_r}{4\pi}\frac{Idl\; sin{90}^{\circ}}{(r^2+a^2)}$$
Where, a is the radius of the circular current carrying loop and r is the distance of the point P from the centre of the loop along the axis.

The direction of $\displaystyle{d\mathbf{B}}$ is perpendicular to LP and along the PQ. Similarly, the magnitude of the magnetic field can be obtained due to the current element $\displaystyle{Idl}$ at the bottom and the direction is along the PQ‘, where $PQ’\perp MP$.

Now, resolving $\displaystyle{d\mathbf{B}}$ due to the current element at L and M. $\displaystyle{d\mathbf{B}cos\phi}$ components balance each other and net magnitude of magnetic field is given as-
\begin{align*}
B&=\oint dBsin\phi\\
&=\oint \frac{\mu_0 \mu_r}{4\pi}\left(\frac{Idl}{r^2+a^2}\right)\cdot\frac{a}{\sqrt{r^2+a^2}}\\
\end{align*}
$$\left[\therefore sin\phi=\frac{a}{\sqrt{r^2+a^2}},\; in\;\Delta{PCL}\right]$$
So after taking all the constant terms out from the integral, we get-
\begin{align*}
B&=\frac{\mu_0 \mu_r}{4\pi}\frac{Ia}{(r^2+a^2)^{\frac{3}{2}}}\oint{dl}\\
&=\frac{\mu_0 \mu_r}{4\pi}\frac{Ia}{(r^2+a^2)^{\frac{3}{2}}}(2\pi a)\\
B&=\frac{\mu_0 \mu_r Ia^2}{2(r^2+a^2)^{\frac{3}{2}}}
\end{align*}
If loop contains N turns of coils then, the magnetic field is given as-
$$B=\frac{\mu_0 \mu_r NIa^2}{2(r^2+a^2)^{\frac{3}{2}}}$$

AT THE CENTRE OF THE LOOP

If we place the point at the centre of the loop then it means value of distance of the point from the centre is zero i.e r = 0. Put r = 0 in the above derived formula, then we get-
\begin{align*}
B&=\frac{\mu_0 \mu_r Ia^2}{2(0^2+a^2)^{\frac{3}{2}}}\\
&=\frac{\mu_0 \mu_r Ia^2}{{2(a^2)}^{\frac{3}{2}}}\\
&=\frac{\mu_0 \mu_r I}{2a}
\end{align*}
If the loop contains N turns of coils, it becomes-
$$\boxed{B=\frac{\mu_0 \mu_r NI}{2a}}$$
Watch this video for more understanding.

Stay tuned with Laws Of Nature for more useful and interesting content.