We know that when electric current flows through the straight current-carrying conductor then it creates a magnetic field that encircles the conductor as shown below:
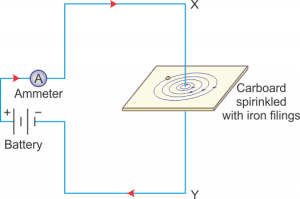
Learn more about magnetic field due to straight current-carrying conductor.
So it is okay that it creates a magnetic field around itself, but my interest is in knowing how we can calculate the strength of this magnetic field.
So in order to calculate the strength of this magnetic field, Jean Baptiste Biot and Flexis Savart have developed a mathematical equation in the year 1820, which is known as Biot-Savart Law. It is very helpful in the calculation of the magnetic field at any arbitrary point P, which lies at a distance r from the current-carrying conductor.
Thus, this article will derive an expression for the magnetic field due to a straight current-carrying conductor. So let’s start…
DERIVATION FOR THE MAGNETIC FIELD DUE TO STRAIGHT CURRENT-CARRYING CONDUCTOR
So going further, let’s recall what Biot-Savart Law states, Biot-Savart Law states that-
The Biot-Savart law states that- the value of the magnetic field at a specific point in space from one short segment of current-carrying conductor is directly proportional to the current element (short segment of current) and to the sine angle (angle between the current direction and vector position of the point), it is also inversely proportional to the square of the distance of the point from the current element Idl.
Mathematically, Biot-Savart Law can be given as-
$$dB\propto\frac{Idl sin\theta}{r^2}$$ and after removing proportionality sign, we get-
$$dB=\frac{\mu_0 \mu_r}{4\pi}\frac{Idl sin\theta}{r^2}$$
Where, $\displaystyle{\mu_0}$ is the absolute permeability of the free space and $\displaystyle{\mu_r}$ is the relative permeability of the medium.
Now let’s come on to derivation–
IF THE CONDUCTOR IS FINITELY LONG
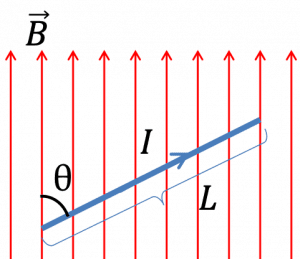
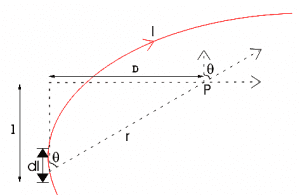
Let’s consider a straight ${I}$ current-carrying conductor of length $l$, on it take a small portion of the conductor ($\displaystyle{dl}$), thus ${I}$ is flowing through the whole conductor then the same current will also flow in that small portion of the conductor, so in this whole article, we will call it as small current element $\displaystyle{Idl}$.
Choose any arbitrary point P in the free space. Take distance vector from the point P to the current element as r and vector displacement as D. And θ is the angle between the direction of current in the small portion and the distance vector, See figure above.
Therefore, we have a small portion of the conductor $\displaystyle{dl}$ then the magnetic field at the point P, due to the current in this small portion of the conductor will be also small i.e $\displaystyle{dB}$. From the Biot-Savart Law the magnetic field at the point P is given as-
$$dB=\frac{\mu_0 \mu_r}{4\pi}\frac{Idl sin\theta}{r^2}$$
Now, the magnetic field at the point P due to the total length of the current-carrying conductor can be represented as-
$$B=\int{dB}$$
$$\implies\; dB=\int{\frac{\mu_0 \mu_r}{4\pi}\frac{Idl sin\theta}{r^2}}$$
$$dB=\frac{\mu_0 \mu_r I}{4\pi}\int{\frac{ sin\theta}{r^2}dl}$$
If D is the perpendicular distance of the point from the wire, then-
$$D=r{sin\theta}\; or\; r=\frac{D}{sin\theta}$$
Now, the magnetic field ($\mathbf{B}$) at the point P can be rewritten as-
\begin{align*}
dB&=\frac{\mu_0 \mu_r I}{4\pi}\int{\frac{ sin\theta}{r^2}dl}\\
&=\frac{\mu_0 \mu_r I}{4\pi}\int{\frac{ sin^{3}\theta}{D^2}dl}
\end{align*}
Thus, the length of the wire is $l$, then from the trigonometry-
$$cot\theta =\frac{l}{D} \implies \; l=D cot\theta$$
Differentiating $\displaystyle{l=D cot\theta}$ with respect to θ, we get-
$$dl=-D csc^{2}\theta d\theta$$
Placing this value of $dl$ in the above equation of magnetic field, we get-
\begin{align*}
B&=\frac{\mu_0 \mu_r I}{4\pi}\int{\frac{ sin^{3}\theta}{D^2}[-D csc^{2}\theta d\theta]}\\
&=-\frac{\mu_0 \mu_r I}{4\pi D}\int{sin^{3}\theta csc^{2}\theta d\theta}\\
&=-\frac{\mu_0 \mu_r I}{4\pi D}\int{sin\theta d\theta}
\end{align*}
The angle θ in the above diagram depends on the length of the wire and the position of the point P. For a certain limited length of the wire, angle θ varies from $\theta_1$ to $\theta_2$. Hence, the magnetic field at point P due to the total length of the conductor is given as-
\begin{align*}
B&=-\frac{\mu_0 \mu_r I}{4\pi D}\int_{\theta_1}^{\theta_2}{sin\theta d\theta}\\
&=-\frac{\mu_0 \mu_r I}{4\pi D}\left[-cos\theta\right]_{\theta_1}^{\theta_2}\\
&=\frac{\mu_0 \mu_r I}{4\pi D}\left[cos\theta_1-cos\theta_2\right]
\end{align*}
IF THE CONDUCTOR IS INFINITELY LONG
If the length of the conductor is infinitely long then θ will varies from 0 to π that is $\theta_1=0$ and $\theta_2=\pi$, after substituting this value in the final expression of magnetic field, we get-
\begin{align*}
B&=\frac{\mu_0 \mu_r I}{4\pi D}\left[cos 0-cos\pi\right]\\
&=\frac{\mu_0 \mu_r I}{4\pi D}\left[1-(-1)\right]=\frac{2\mu_0 \mu_r I}{4\pi D}\\
&=\frac{\mu_0 \mu_r I}{2\pi D}
\end{align*}
So this is the required derivation for the magnetic field due to a straight current-carrying conductor of finite and infinite length.
Stay tuned with Laws Of Nature for more useful and interesting content.