Charge-to-mass ratio of electron, chemistry class 11 NCERT

The charge-to-mass ratio of electrons is a fundamental property of the electron that has played a crucial role in our understanding of the atomic and subatomic worlds. This ratio refers to the amount of electrical charge an electron possesses relative to its mass, and it has been measured with great precision over the years. In this article, we will explore an electron’s charge-to-mass ratio in detail, including its historical background, how it is measured, and its significance in modern physics.

By the end of this post, you will have a solid understanding of this fundamental property of the electron and how it contributes to our understanding of the universe. So, whether you’re an 11th-class student studying chemistry/physics or simply someone interested in the workings of the subatomic world, read on to discover more about the charge-to-mass ratio of electrons.

Charge-to-mass ratio of electron: Historical background

The history of the electron begins with the ancient Greek philosopher Democritus, who proposed the concept of atoms as the fundamental building blocks of matter. However, it was not until the late 19th century that the electron was discovered as a subatomic particle with a negative charge.

In 1897, British physicist J.J. Thomson conducted a series of experiments that led to the discovery of the electron. Thomson used a cathode ray tube to observe a beam of negatively charged particles, which he called “corpuscles.” He concluded that these corpuscles were a fundamental constituent of matter and that they had a much smaller mass than the hydrogen atom, the lightest known element at the time.

Thomson’s discovery of the electron revolutionized our understanding of the atomic structure and led to the development of the first model of the atom, known as the “plum pudding” model. This model proposed that the atom was a sphere of positive charge, with negatively charged electrons embedded within it like raisins in a pudding.

One of the key properties of the electron that Thomson discovered was its charge-to-mass ratio, which he calculated by measuring the deflection of the corpuscles in a magnetic field. Thomson’s calculation of the charge-to-mass ratio of the electron was a significant breakthrough in the study of subatomic particles and paved the way for future discoveries in the field of particle physics.

Overall, the discovery of the electron and the subsequent study of its properties have played a critical role in shaping our understanding of the atomic and subatomic worlds, and have contributed greatly to the advancement of modern physics.

Read Also:

• Cathode Tube Ray Experiment class 11: working, procedure, observation, and conclusion
• Discovery of Electron class 11: chemistry, NCERT

What is an electron, and its properties?

An electron is a subatomic particle that carries a negative electric charge. It is one of the fundamental particles that make up matter, along with protons and neutrons.

Electrons are located outside of the atomic nucleus in regions known as electron shells, and they are responsible for chemical reactions and electrical conductivity.

Some of the key properties of electrons include:

1. Charge: Electrons carry a negative charge equal to $-1.602 \times 10^-19$ coulombs. This charge is opposite in sign to the positive charge carried by protons.
2. Mass: Electrons have a much smaller mass than protons and neutrons. The mass of an electron is approximately $9.11 x 10^-31$ kilograms.
3. Spin: Electrons have a property known as spin, which can be either “up” or “down.” The spin of an electron plays a role in its magnetic properties and its interactions with other particles.
4. Energy: Electrons exist in discrete energy levels within an atom. When an electron absorbs energy, it can move to a higher energy level, and when it releases energy, it can move to a lower energy level.
5. Wave-particle duality: Electrons exhibit wave-like properties, such as diffraction and interference, in addition to their particle-like behavior. This property is a fundamental aspect of quantum mechanics.

Charge-to-mass ratio of electron

The “Charge to Mass Ratio of Electron” (e/m) refers to the ratio of the charge of an electron to its mass. This quantity is an important characteristic of the electron, and it can be determined experimentally by observing the behavior of electrons in a magnetic field.

The mathematical expression for the charge-to-mass ratio of an electron is: $$\frac{e}{m}=\frac{v}{B r}$$

Where $e$ is the charge of an electron, $m$ is the mass of the electron, $v$ is the velocity of the particle, $B$ is the magnetic field strength, and $r$ is the radius of the circular path that the electron follows due to the magnetic force.

J.J. Thomson was the first scientist to measure the charge-to-mass ratio of an electron in 1897. He used a cathode ray tube to produce a beam of electrons and then subjected the beam to a magnetic field. By measuring the deflection of the beam, he was able to determine the charge-to-mass ratio of the electrons.

Thomson’s experimental value for the charge-to-mass ratio of an electron was: $$\frac{e}{m}=1.76 \times 10^{11} C/kg$$

This value has been refined over time through further experiments, and the currently accepted value for the charge-to-mass ratio of an electron is: $$\frac{e}{m}=1.758820024 \times 10^{11} C/kg$$

This value is used in a wide range of applications in physics and engineering, including in the design of electron beams and in the study of atomic and subatomic particles.

Read Also:

• Percentage composition chemistry class 11: formula, definition, examples, NCERT
• Mole concept class 11 | definition, formula & solved examples, NCERT
• Uncertainty in measurement chemistry, class 11 NCERT
• Empirical formula & molecular formula: chemistry class 11

Derive the formula for Charge-to-Mass Ratio of Electron

When an electron moves through a uniform magnetic field, it experiences a magnetic force that acts perpendicular to both its velocity and the magnetic field direction. This force causes the electron to move in a circular path with a radius $r$. The centripetal force required to keep the electron moving in a circle is provided by the magnetic force, which is given by: $$F_B=\frac{m v^2}{r}$$

where $m$ is the mass of the electron, $v$ is its velocity, and $r$ is the radius of the circular path. The magnetic force on an electron can also be expressed in terms of its charge and the magnetic field strength $B$, as follows: $$F_B=e v B$$

where $e$ is the charge of the electron and $v$ is its velocity.

Equating these two expressions for the magnetic force, we get: $$\frac{m v^2}{r}=e v B$$

Solving for $\displaystyle\frac{e}{m}$, we get: $$\frac{e}{m}=\frac{v}{B r}$$

To determine $v$, we can use the fact that the electron is accelerated from rest through a potential difference $V$. The kinetic energy gained by the electron is equal to the potential energy difference, so we have: $$\frac{1}{2} m v^2=e V$$

Solving for $\mathrm{v}$, we get:
$$v=\sqrt{\frac{2 e V}{m}}$$
Substituting this expression for $\mathrm{v}$ into the equation for $\displaystyle\frac{e}{\mathrm{m}}$, we get:
$$\frac{e}{m}=\frac{\sqrt{\frac{2 e V}{m}}}{B r}$$
Simplifying this expression, we get:
$$\frac{e}{m}=\frac{2 V}{B^2 r^2}$$
This is the final expression for the charge-to-mass ratio of an electron, and it shows that this ratio is proportional to the accelerating voltage applied to the electron, and inversely proportional to the square of the magnetic field strength and the square of the radius of the electron’s circular path in the magnetic field.

Experimental setup for the determination of the charge-to-mass ratio of the electron

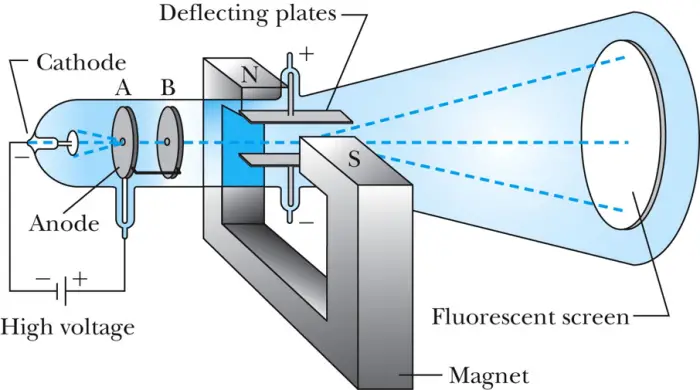
The determination of the charge-to-mass ratio of the electron was an important experiment in the development of modern physics. The experiment was performed by J.J. Thomson in 1897, using a cathode ray tube and a magnetic field. The following is a brief description of the experimental setup:

1. Cathode Ray Tube: The cathode ray tube consists of a vacuum-sealed glass tube that contains an electron gun at one end and a fluorescent screen at the other end. The electron gun emits a stream of electrons that travel through the tube toward the screen.
2. Electromagnet: A strong magnetic field is created using an electromagnet, which is placed around the cathode ray tube. The magnetic field is perpendicular to the path of the electrons, causing them to travel in circular paths.
3. Power Supply: A high-voltage power supply is used to accelerate the electrons toward the screen. The accelerating voltage can be varied to change the speed of the electrons.
4. Fluorescent Screen: A fluorescent screen is placed at the end of the cathode ray tube. When the electrons hit the screen, they produce a visible spot that can be observed and measured.

By varying the magnetic field strength and the accelerating voltage, J.J. Thomson was able to measure the radius of the circular paths that the electrons followed. From these measurements, he was able to calculate the charge-to-mass ratio of the electron using the formula: $$\frac{e}{m}=\frac{2 V}{B^2 r^2}$$

where $e$ is the charge of the electron, $m$ is its mass, $V$ is the accelerating voltage, $B$ is the magnetic field strength, and $r$ is the radius of the circular path.

Thomson’s experiment provided the first direct measurement of the charge-to-mass ratio of the electron, which was found to be approximately $1.76 \times 10^{11}$ coulombs per kilogram. This experiment paved the way for further discoveries in the field of atomic and particle physics.

Watch this video for more reference:

Significance of charge-to-mass ratio of the electron

The charge-to-mass ratio of the electron has significant implications in the field of physics. Here are some of the important applications and significance of the charge-to-mass ratio of the electron:

1. Determination of the mass of the electron: The charge-to-mass ratio of the electron played a key role in the determination of the mass of the electron. By measuring the charge-to-mass ratio of the electron and knowing the charge of the electron, scientists were able to calculate the mass of the electron.
2. Understanding the nature of cathode rays: Cathode rays were discovered in the early 19th century and were initially thought to be some sort of electromagnetic radiation. However, J.J. Thomson’s experiments with cathode rays, in which he determined the charge-to-mass ratio of the electron, showed that they were actually streams of negatively charged particles.
3. Development of electron-based technologies: The understanding of the charge-to-mass ratio of the electron led to the development of numerous electron-based technologies, such as the cathode ray tube, electron microscopes, and particle accelerators.
4. Advancements in nuclear physics: The charge-to-mass ratio of the electron is also significant in the field of nuclear physics. By understanding the charge-to-mass ratios of various subatomic particles, scientists are able to study the structure of atomic nuclei and the interactions between subatomic particles.

Overall, the charge-to-mass ratio of the electron played a crucial role in advancing our understanding of the nature of matter and the development of modern technologies.

Frequently Asked Questions – FAQs

Stay tuned with Laws Of Nature for more useful and interesting content.