Inside Story

SIMILARITIES AND DIFFERENCE BETWEEN BIOT-SAVART LAW AND COULOMB’S LAW

In this article, we are going to discuss about similarities and differences between Biot-Savart Law and coulomb’s law. So let’s start…

Both laws are used to measure the different quantities, one measures the electrostatic force then the other measures the magnetic field. Coulomb’s law measures the forces between two static charges whereas Biot-Savart Law is used to measure the magnetic field when the charges are in motion.

So before listing similarities and differences, let’s take a brief snapshots about coulomb’s law and Biot-Savart Law. [latexpage]

COULOMB’S LAW

It is a very important law of electrostatic. It is analogy to universal law of gravitation. Coulomb’s law tells that how does two electric charges interact with each other and on what factors their interactions depends upon. If there is two stationary charges $q_1$ and $q_2$ seperated by the distance $r$, then

According to Coulomb’s Law-

Electrostatic force is directly proportional to product of two charges i.e $\displaystyle{F\propto q_1 q_2}$.
Electrostatic force is inversely proportional to square of distance between two charges i.e $\displaystyle{F\propto\frac{1}{r^2}}$.
Combining all, we get $\displaystyle{F\propto\frac{q_1 q_2}{r^2}}$.
Removing proportionality sign we get $\displaystyle{F=k\frac{q_1 q_2}{r^2}}$, where k is called electrostatic constant whose value in vaccum is $\displaystyle{k=8.85\times 10^{-12}C^2/Nm^2}$.
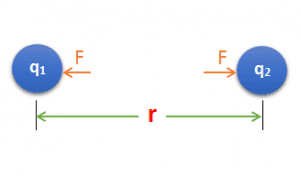
Fig. 1, coulomb’s law – force between two static charges, source: swiftutors.com

BIOT-SAVART LAW

It is a very important law of electrodynamics. It is analogy to coulomb’s law. This law tells about the magnetic field at a point from the current carrying conductor and about the factors on which this magnetic field depends upon. According to Biot-Savart Law.

If a conductor is carrying current $I$ then the magnetic field at a point P due to infinitesimal portion of wire $dl$ will depends upon the following factors.

$\displaystyle{dB\propto I}$
$\displaystyle{dB\propto dl}$
$\displaystyle{dB\propto sin\theta}$

$\displaystyle{dB\propto \frac{1}{r^2}}$
Combining all, we get $\displaystyle{dB \propto\frac{Idl\;sin\theta}{r^2}}$
After removing proportionality sign, we get- $\displaystyle{dB= k\frac{Idl\;sin\theta}{r^2}}$, where k is called magnetic constant, whose value is $\displaystyle{10^{-7}N/A^2}$
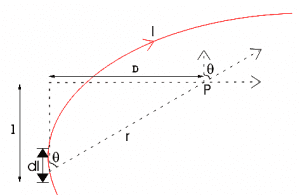
Fig. 2, Biot-Savart Law, source: electrical4u.com

So, after recalling coulomb’s law and Biot-Savart Law. Now let’s talk about their similarities and differences.

SIMILARITIES BETWEEN COULOMB’S LAW AND BIOT-SAVART LAW

Some similarities between coulomb’s law and Biot-Savart Law is listed below:

Both the electric and magnetic field follows the inverse square law.
Both the electric and magnetic field have the long-ranges effect.
Both the electric and magnetic field obey the Superposition Principle.

Both the electric and magnetic field have the linear source, magnetic field depends upon $Idl$ (current element), whereas electric field depends upon q (electric charges).

DIFFERENCE BETWEEN COULOMB’S LAW AND BIOT-SAVART LAW

Some differences between them is listed below:

The electric charge element $dq$ producing electric field is a scalar source whereas the electric current element $Idl$ producing magnetic field is a vector source having direction as directed by the right hand thumb rule.

In Biot-Savart Law, the value of magnetic field depends upon the sine of angle θ between the distance vector r and direction of the current in infinitesimal portion $Idl$, but there is no such angle dependency for electric field.
Electric field is always directed along the displacement vector joining the source and the point at which electric field is to be calculated, but the magnetic field is always perpendicular to the distance vector $r$ and the current element $Idl$ i.e cross product between $dl\times r$ gives the direction of magnetic field.
The relationship between the constant involved in the coulomb’s law and Biot-Savart Law is given as- $$\mu_0 \varepsilon_0=\frac{1}{c^2}$$ where, $\mu_0$ is the absolute permeability of the free space, $\varepsilon_0$ is the absolute permittivity of the free space and c is the speed of light in vaccum.