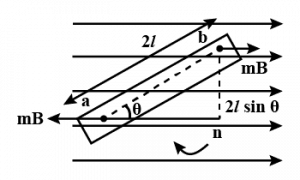Torque experienced by a current loop
In this article, we will discuss and derive an expression for torque experienced by a current-carrying loop in a uniform magnetic field. So without any delay, let’s get started…[latexpage]
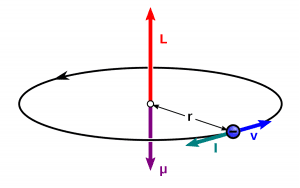
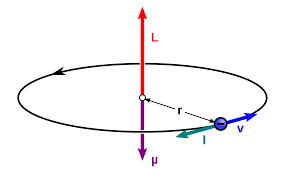
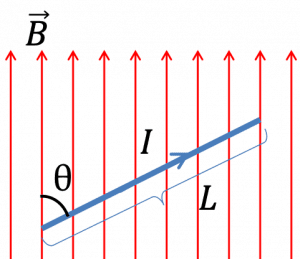
Let’s consider a rectangular loop $ABCD$, suspended in a uniform magnetic field $B$. Let $AB = CD = b$ is the breadth of the rectangular loop and $AD = BC = a$ is the length of the rectangular loop. Let $I$ is the current flowing through the loop.

Case – 1: When rectangular loop is placed such that the uniform magnetic field B is in the plane of the loop
No magnetic force is exerted by the magnetic field on the arm $AD$ and $BC$, it is because they are parallel to the magnetic field. The magnetic force $F_1$ exerted on the arm $AB$ is – $$F_1=IbB$$ and the magnetic force $F_2$ exerted on the arm $CD$ is – $$F_2=IbB=F_1$$
$F_1$ and $F_2$ are equal and opposite, so the net force on the loop is zero. But the line of action of $F_1$ and $F_2$ are opposite and parallel, so they form a couple.
The torque acting due to the couple on the loop rotates the loop in the anticlockwise direction. It is the same as you apply the equal and opposite force on the bottle cap to open it. The opening of the bottle cap is the best example of coupling. This couple rotates the bottle cap around the mouth of the bottle.
The torque acting due to the couple on the loop is given as- $$\tau=F_1\frac{a}{2}+F_2\frac{a}{2}$$ Therefore torque is defined as the product of force and perpendicular distance of the line of action i.e torque = force × perpendicular distance of the line of action.
\begin{equation*}\begin{split}\tau&=IbB\frac{a}{2}+IbB\frac{a}{2}\\ \tau&=I(ab)B\\ &\boxed{\tau=IAB}\end{split}\end{equation*}
Suggested readings:-
- Magnetic dipole moment of a current-carrying loop.
- Magnetic dipole moment of a bar magnet
- Magnetic moment in terms of magnetization
- Magnetic moment class-12, definition, units, and measurement
- Torque experienced by an electric dipole kept in the uniform external electric field
Case -2: When the plane of the loop is not along the magnetic field but makes an angle θ with it
Let the angle between the magnetic field and the normal of the loop is θ. Forces on $BC$ and $DA$ are equal and opposite, so they cancel each other as they are collinear.
Force on $AB$ is $F_1$ and force on $CD$ is $F_2$. $$F_1=F_2=IbB$$ Magnitude of the torque on the loop as shown in figure below is –
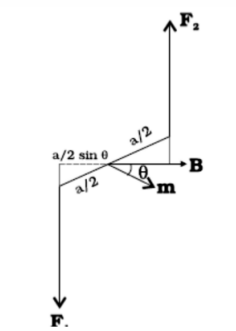
\begin{equation*}\begin{split}\tau&=F_1\frac{a}{2}\sin\theta + F_2\frac{a}{2}\sin\theta\\\tau&=IabB\sin\theta=IAB\sin\theta\end{split}\end{equation*} where $A=ab$ (area of the loop).
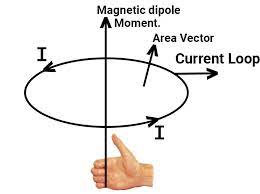
Torque in the terms of magnetic moment (M)
The torque on the loop can be expressed as the vector product of the magnetic moment of the loop and the magnetic field. $$\tau=MB\sin\theta{\hat{\mathbf{n}}}=M\times B$$ where $M=IA$ is the magnetic moment of the loop, and it’s unit is $A.m^2$. When $M$ and $B$ are parallel then the current loop is in the stable equilibrium. Any small rotation of the loop produces a torque $\tau$, which brings it back to its original position. But when $M$ and $B$ are in antiparallel, then the current loop is in unstable equilibrium. The magnetic moment of the loop is given as- $$M= IA$$
Suppose, we replace the single loop of current with a coil on N turns. Then, the turns form a flat coil, and the torque ($\tau$) with the magnitude given in the above equation for torque acts on each of them. The total amount of torque acted on the coil is given by- \begin{equation*}\begin{split}\tau&=N\tau=NIAB\sin\theta\\ \tau&= (NIA)B\sin\theta=NMB\sin\theta\end{split}\end{equation*} Watch this video for more understanding.
Stay tuned with Laws Of Nature for more useful and interesting content.