Magnetic moment in terms of angular momentum
In this article, we will discuss the magnetic moment of revolving electrons around the nucleus of a hydrogen atom in terms of angular momentum, so let’s get started…
In Bohr’s model of the hydrogen atom, the electron revolves in a circular orbit around the proton (a dense central particle). [latexpage] When an electron revolves around the nucleus, it passes a particular point on the loop in a certain period of time, so we can calculate the electric current as follows: $$I=\frac{Q}{T}$$
If it is revolving and producing electric current then we can consider it as the current flowing in the circular loop. In the study of magnetism, we have seen that a current-carrying wire produces magnetic fields. It is, therefore, also reasonable to conclude that the hydrogen atom produces a magnetic field due to revolving electrons, and interacts with other magnetic fields.
There are two pictures below, in which, (a) Current flowing through a circular wire is analogous to (b) an electron that orbits a proton in a hydrogen atom.
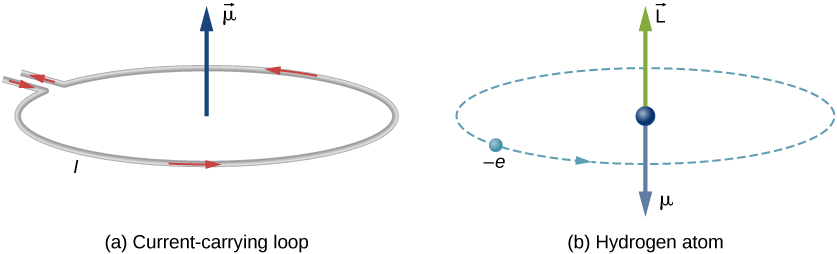
The orbital magnetic dipole moment is a measure of the strength of the magnetic field produced by the orbital angular momentum of an electron. From Force and Torque on a Current Loop, the magnitude of the orbital magnetic dipole moment for a current loop is given as- $$\mu = IA$$ where I is the current and A is the area of the loop. The current I associated with an electron in orbit about a proton in a hydrogen atom is $$I=\frac{e}{T}$$ where e is the magnitude of the electron charge and T is its orbital time period. If we assume that the electron travels in a perfectly circular orbit, then the orbital time period is- $$ T=\frac{2\pi r}{v}$$ where r is the radius of the orbit and v is the speed of the electron in its orbit, given that the area of a circle is $\pi {r}^{2}$, so, therefore, the absolute magnetic moment of a revolving electron around the nucleus of a hydrogen atom is given as- $$\mu =IA=\frac{e}{\frac{2\pi r}{v}}\cdot \pi {r}^{2}$$ $$\mu =\frac{evr}{2}…(1)$$
In terms of angular momentum
We can easily express this magnetic moment ($\mu$) in terms of orbital angular momentum $(\vec{L}=\vec{r}\times \vec{p}$, because the electron revolves in a circular orbit, the position vector $\vec{r}$ and the momentum vector $\vec{p}$ form a right angle. Thus, the magnitude of the orbital angular momentum is given as- $$L=|\vec{L}|=|\vec{r}\times \vec{p}|=rp\sin\theta = mvr $$
Multiplying numerator and denominator by mass of the electron $(m_{e})$, we get- $$\mu=\frac{e}{2m_{e}}\cdot {mvr}=\frac{e}{2m_{e}}{L}$$
In vector form, it can be given as- $$\mu= -\left(\frac{e}{2m_{e}}\right){\vec{L}}$$ Here, you can see, there is a negative sign, it is because electron has the negative charge. Due to this negative sign, the direction of the magnetic moment of the electron is antiparallel to the orbital angular momentum, see figure below:

In bohr atomic model, the relationship between the $\mu$ and $\vec{L}$ is independent of the radius of the orbit. The relationship between the magnetic moment and orbital angular momentum ($l$) can be given as- $$\mu= \left(\frac{e}{2m_{e}}\right){L}=\left(\frac{e}{2m_{e}}\right)\sqrt{l(l+1)\hbar}$$ $$=\mu_{B}\sqrt{l(l+1)}$$ The z components of the magnetic moment is- $$\displaystyle{\mu= \left(\frac{e}{2m_{e}}\right){L_z}= \left(\frac{e}{2m_{e}}\right){m\hbar}=\mu_{B}{m}}$$
The quantity $\mu_B$ is the fundamental unit of magnetism called the Bohr magneton. It’s value is $9.3\times 10^{-34}\;joule/\;tesla$ or $5.8\times 10^{-5}eV/T$. The formula which we derived above for the magnetic moment is not the complete formula because the total magnetic dipole moment of the hydrogen atom is due to both the orbital motion of the electron and its intrinsic spin, in this article we are not going to discuss the spin effects. we will discuss electron spin and its effect on the magnetic dipole moment in some other article in detail, but for now, ignore it.
Stay tuned with Laws Of Nature for more useful and interesting content.