In this article, we will discuss the grouping of inductors i.e. inductors in series & parallel, class 12. So let’s get started…
Grouping of inductors
When two and more inductors are combined in an electrical circuit to give an equivalent output is called grouping of inductors. Grouping of inductors can be done in any circuit by the following two means, i.e.
- Inductors in series
- Inductors in parallel
Read Also
- Derivation for mutual inductance of two long co-axial solenoids
- Mutual inductance – definition, formula, units, and dimensions
Inductors in series
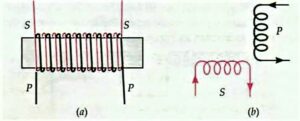
Inductors in series: (1). Let the series combinations of inductors be such that the current flows in the same sense in both the inductors. See the figure below.
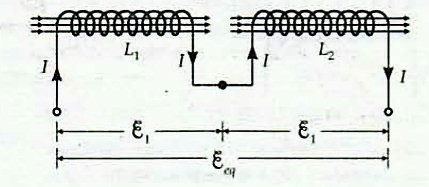
Let $L_{e q}$ be the equivalent inductance of the two self-inductances $L_{1}$ and $L_{2}$ connected in series. For the series combination, the emfs induced in the two coils get added up. Thus $$ \varepsilon_{e q}=\varepsilon_{1}+\varepsilon_{2} $$ If the rate of change of current in the series circuit is $\frac{d I}{d t}$, then $$ \begin{aligned} &\varepsilon_{1}=-L_{1} \frac{d I}{d t}-M \frac{d I}{d t}, \\ &\varepsilon_{2}=-L_{2} \frac{d I}{d t}-M \frac{d I}{d t} \end{aligned} $$ and $$ \varepsilon_{e q}=-L_{e q} \frac{d I}{d t} $$ The negative sign throughout indicates that both self and mutual induced emfs are opposing the applied emf. Using the above equations, we have $$ \varepsilon_{e q}=\varepsilon_{1}+\varepsilon_{2} $$ or $$ -L_{e q} \cdot \frac{d I}{d t}=-\left(L_{1}+M+L_{2}+M\right) \frac{d I}{d t} $$ or $$ L_{\text {eq }}=L_{1}+L_{2}+2 \mathrm{M} \text {. } $$
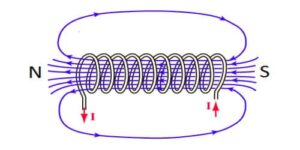
(2). Let the series combinations of inductors be such that the current flows in the opposite sense in both the inductors. See the figure below.
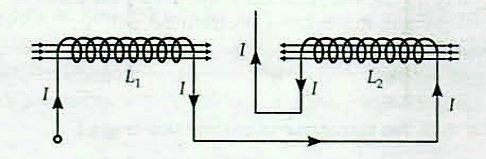
The EMFs induced in the two coils will be
$$
\begin{aligned}
&\varepsilon_{1}=-L_{1} \frac{d I}{d t}+M \frac{d I}{d t}, \\
&\varepsilon_{2}=-L_{2} \frac{d I}{d t}+M \frac{d I}{d t}
\end{aligned}
$$
Here the mutual EMFs act in the direction of applied emf and are hence positive. The EMFs induced in the two coils get added for this series combination.
Hence $\varepsilon_{e q}=\varepsilon_{1}+\varepsilon_{2}=-\left[L_{1}-M+L_{2}-M\right] \frac{d I}{d t}$
But $\quad \varepsilon_{e q}=-L_{e q} \frac{d I}{d t}$
$$
\therefore \quad-L_{\mathrm{eq}} \frac{d I}{d t}=-\left[L_{1}+L_{2}-2 M\right] \frac{d I}{d t}
$$
or
$$
L_{e q}=L_{1}+L_{2}-2 M \text {. }
$$
Inductors in series calculator
Inductors in parallel
Inductors in parallel: In parallel combinations of inductors, the total current $I$ divides into both the inductors $(I_1\; \text{and} \;I_2)$ such that the sum of both of the currents remains the same as of original.
Read Also
$$\begin{aligned} I &=I_{1}+I_{2} \\ \therefore \quad \frac{d I}{d t} &=\frac{d I_{1}}{d t}+\frac{d I_{2}}{d t} \end{aligned}$$
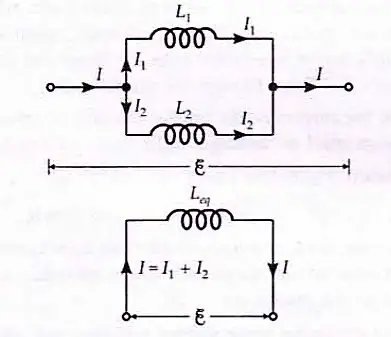
For parallel combination, induced emf across the combination is equal to the induced emf across each inductance. Thus $$ \begin{aligned} &\varepsilon=-L_{1} \frac{d I_{1}}{d t} \quad \text { or } \quad \frac{\varepsilon}{L_{1}}=-\frac{d I_{1}}{d t} \\ &\varepsilon=-L_{2} \frac{d I_{2}}{d t} \quad \text { or } \quad \frac{\varepsilon}{L_{2}}=-\frac{d I_{2}}{d t} \end{aligned} $$ This is because the mutual inductance $M$ is negligible. If $L_{e q}$ is the equivalent inductance of the parallel combination, then $$ \begin{aligned} \varepsilon &=-L_{e q} \cdot \frac{d I}{d t}=-L_{e q}\left[\frac{d I_{1}}{d t}+\frac{d I_{2}}{d t}\right] \\ &=L_{e q}\left[-\frac{d I_{1}}{d t}-\frac{d I_{2}}{d t}\right] \end{aligned} $$ or $\displaystyle{\frac{\varepsilon}{L_{e q}}=\left[\frac{\varepsilon}{L_{1}}+\frac{\varepsilon}{L_{2}}\right]}$, or $\displaystyle{\frac{1}{L_{e q}}=\frac{1}{L_{1}}+\frac{1}{L_{2}}}$, or $\displaystyle{\quad L_{e q}=\frac{L_{1} L_{2}}{L_{1}+L_{2}}}$
If there is any mutual inductance $M$ between the coils, then $$ L=\frac{L_{1} L_{2}-M^{2}}{L_{1}+L_{2} \pm M} . $$
Read Also
- Formula for energy stored in the inductor, class 12
- Self-inductance | definition, formula, units, and dimensions
Inductors in parallel calculator
Stay tuned with Laws Of Nature for more useful and interesting content.