In this short piece of article, we will obtain an expression of self-inductance of a long solenoid. So let’s get started…
Expression for Self-inductance of a long solenoid
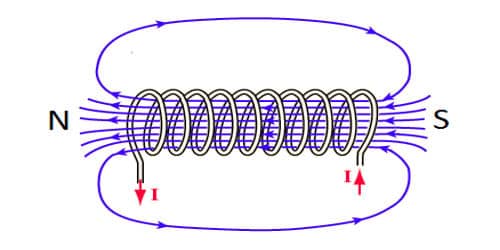
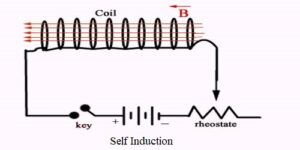
Self-inductance of a long solenoid. Consider a long solenoid of length $l$ and radius $r$ with $r<<l$ and having $n$ turns per unit length. If a current $I$ flows through the coil, then the magnetic field inside the coil is almost constant and is given by $$ B=\mu_{0} n I $$ Magnetic flux linked with each turn $$ =B A=\mu_{0} n I A $$ where $A=\pi r^{2}=$ the cross-sectional area of the solenoid. $\therefore$ Magnetic flux linked with the entire solenoid is $\phi=$ Flux linked with each turn $\times$ total number of turns $$ =\mu_{0} n I A \times n l=\mu_{0} n^{2} l A I $$ But $\phi=L I$ $\therefore$ Self-inductance of the long solenoid is $$ L=\mu_{0} n^{2} l A $$ If $N$ is the total number of turns in the solenoid, then $n=N / l$ and so $$ L=\frac{\mu_{0} N^{2} A}{l} $$ If the coil is wound over a material of high relative magnetic permeability $\mu_{r}$ (e.g., soft iron), then $$ L=\mu_{r} \mu_{0} n^{2} l A=\frac{\mu_{r} \mu_{0} N^{2} A}{l} . $$
Read Also
Factors affecting self-inductance
The self-inductance of a solenoid depends on its geometry and the magnetic permeability of the core material.
- The number of turns. The larger the number of turns in the solenoid, the larger its self-inductance. $$ L \propto N^{2} $$
- Area of the cross-section. The larger the area of the crosssection of the solenoid, the larger its self-inductance. $$L \propto A$$
- Permeability of the core material. The self-inductance of a solenoid increases $\mu_{r}$ times if it is wound over an iron core of relative permeability $\mu_{r}$.
Read Also
- Self-inductance | definition, formula, units, and dimensions
- Inductance – definition, formula, units, and dimensions
Frequently Asked Questions – FAQs
What is the formula for the self-inductance of a solenoid?
The formula for the self-inductance of a solenoid is L = μr μ0 n2 A l
Does self-inductance depend on length?
Self-inductance of the coil depends on the area of cross-section of the coil, the number of turns per unit length in the coil, the length of the solenoid, and the permeability of the core material.
What is a long solenoid?
A solenoid is a type of electromagnet, which is used to generate a controlled magnetic field through a coil that is wound into a tightly packed helix. The coil can be arranged in such that it produces a uniform magnetic field in a volume of space when an electric current is passed through it
How do you increase the self-inductance of a solenoid?
We can also increase inductance by increasing the diameter of the coil or making the core longer. Increasing the number of coil turns. In both cases, more wire is required to construct the coil, and therefore, more lines of force exist to produce the required back emf.
What is self-inductance?
Self-inductance is the tendency of a coil to resist changes in current in itself. Whenever current changes through a coil, they induce an EMF, which is proportional to the rate of change of current through the coil.




Sweet explanation