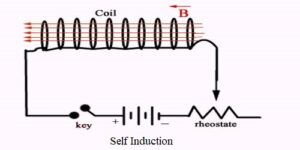
In this article, we will derive an expression for the mutual inductance of two long coaxial solenoids. So let’s get started…
What is mutual inductance?
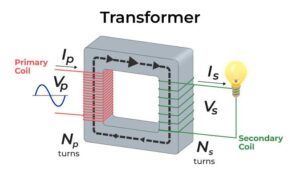
Mutual inductance is a phenomenon in which an emf is induced in the secondary coil by changing the current in the primary coil.
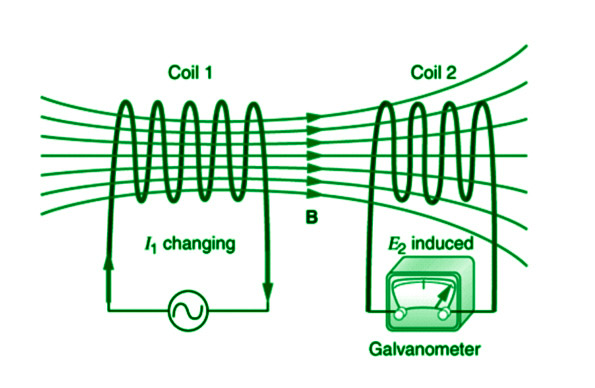
Here, there are two coils i.e coil1 and coil2. You can see in the above diagram that coil2 is kept in the region of the magnetic field of the primary coil (coil1). Now, whenever we change the current $(I_1)$ in the coil1, the magnetic field generated due to this also changes. If the current in the coil1 is continuously changing then the magnetic field due to this will be also continuously changing.
Coil2 is kept in the region of the continuously changing magnetic field of coil1. This changing magnetic field linked a changing magnetic flux to the coil2. From Faraday’s law of electromagnetic induction, changing magnetic flux induces an emf across the coil.
Read Also
- Mutual inductance – definition, formula, units, and dimensions
- Formula for energy stored in the inductor, class 12
Mathematically,
Let $N_1$ and $N_2$ are the number of turns in the coil1 and coil2, and $I_1$ be the current flowing in the coil1. The magnetic flux linked to the coil2 due to the current $I_1$ is $\phi_{21}$. If $I_1$ is the changing current in the coil1 then the magnetic flux due to this, linked to the coil2 is also a changing one. From Faraday’s laws of electromagnetic induction, this changing magnetic flux linked to the coil2 $(\phi_{21})$ induces an emf in the coil2. $$\varepsilon_{21}=-N_2\frac{d\phi_{21}}{dt}$$
The induced emf in coil2 is directly proportional to the current that passes through coil1. i.e. $${{N}_{2}}\,{{\phi }_{21}}\propto {{I}_{1}}$$ $${{N}_{2}}\,{{\phi }_{21}}={{M}_{21}}{{I}_{1}}$$ The constant of proportionality is called as mutual inductance. It can be written as; $${M}_{21}=\frac{{N}_{2}\phi_{21}}{I_1}$$
The SI unit of inductance is henry $(\mathrm{H})$
$$1 H=\frac{1\left(\text { Tesla) } \cdot 1\left(m^{2}\right)\right.}{1 A}$$
In a similar manner, the current in coil2, $\mathrm{I}_{2}$ can produce an induced emf in coil 1 when $\mathrm{I}{2}$ is varying with respect to time. Then,
$$\varepsilon_{12}=-N_{1} \frac{d \phi_{12}}{d t}$$ The induced emf in coil1 is directly proportional to the current that passes through coil2. i.e.
$$N_{1} \phi_{12} \propto I_{2}$$
$$N_{1} \phi_{12}=M_{12} I_{2}$$
$$M_{12}=\frac{N_{1} \phi_{12}}{I_{2}}$$
This constant of proportionality is another mutual inductance.
Derivation for mutual inductance of two long co-axial solenoids
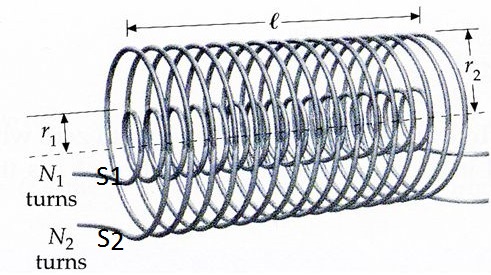
The mutual inductance of two coils is equal to the e.m.f. induced in one coil when the rate of change of current through the other coil is unity.
Mutual inductance of two co-axial solenoids:
Consider two long co-axial solenoids each of length $l$ with a number of turns $N_{1}$ and $N_{2}$ wound one over the other. Number of turns per unit length in solenoid, $n=\frac{N_{1}}{l}$. If $I_{1}$ is the current flowing in the primary solenoid, the magnetic field is produced within this solenoid.
$$
B_{1}=\frac{\mu_{0} \mathrm{~N}_{1} \mathrm{I}_{1}}{l}
$$
The flux linked with each turn of the inner solenoid coil is $\phi_{2}=B_{1} A_{2}$, where $A_{2}$ is the cross-sectional area of the inner solenoid. The total flux linkage with the inner coil of $\mathrm{N}_{2}$ turns.
$$
\begin{aligned}
\phi_{2} &=N_{2} \phi_{2}\\
&=N_{2} B_{1} A_{2}\\
&=N_{2}\left(\frac{\mu_{0} N_{1} I_{1}}{l}\right) A_{2}\\
&=\frac{\mu_{0} N_{1} \mathbf{N}_{2} A_{2} I_{1}}{l}
\end{aligned}
$$
Mutual Inductance, $\mathrm{M}_{21}=\frac{\phi_{2}}{I_{1}}=\frac{\mu_{0} \mathrm{~N}_{1} \mathrm{~N}_{2} \mathrm{~A}_{2}}{l}$ If $n_{1}$ is number of turns per unit length of outer solenoid and $r_{2}$ is radius of inner solenoid, then
$$
\mathbf{M}=\mu_{0} n_{1} \mathbf{N}_{2} \pi r_{2}^{2}
$$
Read Also
- Lenz’s law – statement, formula, application, and experiments
- Electromagnetic induction | definition, applications, and history
Reciprocity Theorem of mutual inductance
$\therefore$ Mutual inductance of coil1 with respect to coil2 is
$$
M_{12}=\frac{\phi_{1}}{I_{2}}=\frac{\mu_{0} N_{1} N_{2} A}{l}
$$
Clearly $M_{12}=M_{21}=M$ (say)
| $$ \therefore \quad M=\frac{\mu_{0} N_{1} N_{2} A}{l}=\mu_{0} n_{1} n_{2} A l=\mu_{0} n_{1} n_{2} \pi r_{1}{ }^{2} l $$ |
Thus, the mutual inductance of two coils is the property of their combination. It does not matter which one of them functions as the primary or the secondary coil. This fact is known as the reciprocity theorem.
Factors affecting mutual inductance
Factors on which mutual inductance depends. The mutual inductance of two solenoids depends on their geometry and the magnetic permeability of the core material.
- The number of turns. The larger the number of turns in the two solenoids, the larger will be their mutual inductance.
$$
M \propto N_{1} N_{2}
$$ - Common cross-sectional area. The larger the common cross-sectional area of two solenoids, the larger will be their mutual inductance.
- Relative separation. The larger the distance between two solenoids, the smaller will be the magnetic flux linked with the secondary coil due to the current in the primary coil. Hence smaller will be the value of $M$.
- Permeability of the core material: If the two coils are wound over the iron core of relative permeability of $mu_r$, then their mutual inductance increases by $mu_r$ times.
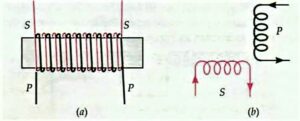
- The relative orientation of the two coils. $M$ is maximum when the entire flux of the primary is linked with the secondary, i.e. when the primary coil completely envelopes the secondary coil. $M$ is the minimum when the two coils are perpendicular to each other, see below.
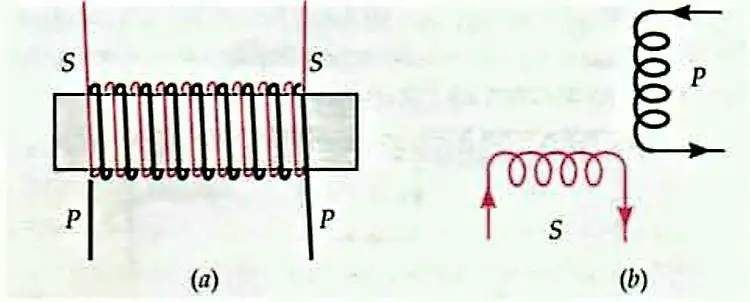
Coefficient of coupling
Coefficient of coupling. The coefficient of coupling of two coils gives a measure of the manner in which the two coils are coupled together. If $L_{1}$ and $L_{2}$ are the self- inductances of two coils and $M$ is their mutual inductance, then their coefficient of coupling is given by $$ K=\frac{M}{\sqrt{L_{1} L_{2}}} $$ The value of $K$ lies between 0 and 1. When the coupling is perfect i.e., the total flux of primary is linked with the secondary, $M$ is maximum, and $K=1$. When there is no coupling, $M=0$ and $K=0$. Thus $K$ is the maximum for the coupling shown in Fig.(a) and the minimum for the coupling shown in Fig. $(b)$ above.
Stay tuned with Laws Of Nature for more useful and interesting content.