Hmmm… Mutual inductance has more self-respect than self-inductance because it has a wide range of applications in electrical engineering. Mutual inductance is the main working principle of generators, motors, transformers, etc.
Self-inductance induces an emf across the coil itself. But in mutual inductance, an emf is generated in the secondary coil by changing the current in the primary coil. In this article, we will talk about Mutual inductance – definition, formula, units, and dimensions in detail, so let’s get started…
What is mutual inductance?
Mutual induction. Mutual induction is the phenomenon of the production of induced emf in one coil due to a change of current in the neighboring coil.
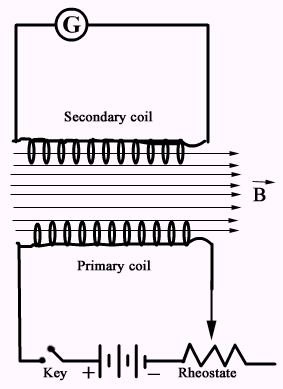
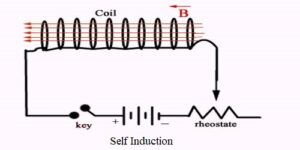
As shown above, consider two coils, where $P$ and $S$ are placed close to each other. The coil $P$ is connected in series to a battery $B$ and a rheostat $R h$ through a tapping key $K$. The coil $S$ is connected to a galvanometer $G$. When a current flows through coil $P$, it produces a magnetic field which produces a magnetic flux through coil $S$.
If the current in the coil $P$ is varied, the magnetic flux linked with the coil $S$ changes which induces an emf and hence a current in it, as is seen from the deflection in the galvanometer. The coil $P$ is called the primary coil and coil $S$, the secondary coil, because it is the former which causes an induced emf in the latter.
Read Also
Coefficient of mutual inductance
Coefficient of mutual induction. At any instant, Magnetic flux linked with the secondary coil $\propto$ current in the primary coil $\text { i.e. } \phi \propto I$ $$\text { or }\qquad \phi=MI\qquad….(1)$$
The proportionality constant $M$ is called the mutual inductance or coefficient of mutual induction of the two coils. Any change in the current $I$ sets up an induced emf in the secondary coil which is given by $$ \varepsilon=-\frac{d \phi}{d t}=-M \cdot \frac{d I}{d t} \qquad…. (2)$$
If in equation (1), $I=1$, then $\phi=M$
Thus the mutual inductance of two coils is numerically equal to the magnetic flux linked with one coil when a unit current passes through the other coil.
Again, from equation (2), if $$ \frac{d I}{d t}=1 \text {, then } \varepsilon=-M $$
The mutual inductance of two coils may be defined as induced emf set up in one coil when the current in the neighboring coil changes at the unit rate.
Unit of mutual inductance
Unit of mutual inductance. From equation (2), we have $$ M=\frac{\varepsilon}{\frac{d I}{d t}} $$ $\therefore$ SI unit of $M=\frac{1 \mathrm{~V}}{1 \mathrm{As}^{-1}}=1 \mathrm{VsA}^{-1}=1$ henry $(\mathrm{H})$
The mutual inductance of two coils is said to be one henry if an induced emf of one volt is set up in one coil when the current in the neighbouring coil changes at the rate of 1 ampere per second.
Dimensions of mutual inductance
We know that
| $$L=\frac{\phi}{I}=\frac{BA}{I}=\frac{F}{qv\sin\theta}.\frac{A}{I},\qquad[\therefore\; F=qv\sin\theta]$$ |
∴ Dimensions of M
| $$=\frac{MLT^{-2}.L^2}{C.LT^{-1}.A}=\frac{ML^{2}T^{-2}}{A.A}=[ML^{2}T^{-2}A^{-2}]$$ |
Demonstration of mutual inductance
Let’s consider that you have two coils viz. coil1 and coil2. Whenever you change the current of coil1, a change in magnetic flux occurs. This change in magnetic flux induces an emf in the coil1 itself that opposes the change in a current called self-inductance.
But when you put a second coil say coil2, in the region of the changing magnetic field of the coil1. This changing magnetic field is linked to coil2 and induces an emf in coil2. This is called mutual inductance.
Read Also
- Self-inductance | definition, formula, units, and dimensions
- Self-inductance of a long solenoid class 12
Watch this video for a practical demonstration of mutual inductance.
Factors affecting mutual inductance
Factors on which mutual inductance depends. The mutual inductance of two solenoids depends on their geometry and the magnetic permeability of the core material.
- The number of turns. The larger the number of turns in the two solenoids, the larger will be their mutual inductance.
$$
M \propto N_{1} N_{2}
$$ - Common cross-sectional area. The larger the common cross-sectional area of two solenoids, the larger will be their mutual inductance.
- Relative separation. The larger the distance between two solenoids, the smaller will be the magnetic flux linked with the secondary coil due to the current in the primary coil. Hence smaller will be the value of $M$.
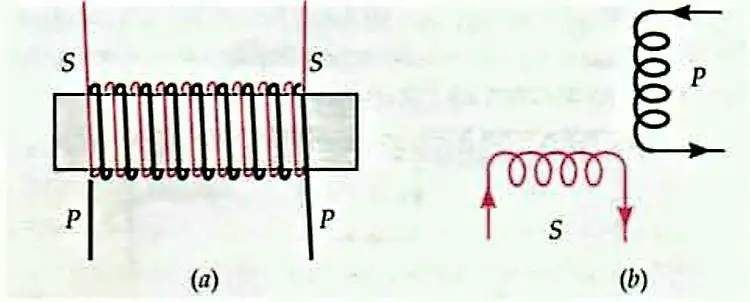
- The relative orientation of the two coils. $M$ is maximum when the entire flux of the primary is linked with the secondary, i.e. when the primary coil completely envelopes the secondary coil. $M$ is the minimum when the two coils are perpendicular to each other, see below.
Uses of mutual inductance
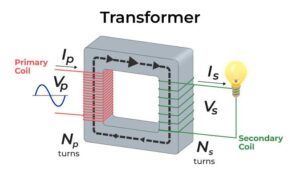
The concept of mutual inductance is used in various electrical machines such as:
- Metal detectors
- Generators
- Transformer
- Radio receiver (for generating high-frequency current)
Frequently Asked Questions – FAQs
What is a mutual induction class 12?
Mutual induction is defined as the property of the coils that enables them to oppose the changes in the current in another coil. With a change in the current of one coil, the flow changes too thus inducing EMF in the other coil. This phenomenon is known as mutual induction.
What is the coefficient of mutual induction?
Coefficient of mutual induction:- It is a measure of the induction between two circuits, It is the ratio of the electromotive force in a circuit to the corresponding change of current in a neighboring circuit; usually measured in henries. $$M=\frac{\varepsilon}{\frac{d I}{d t}}$$
What is one-henry mutual inductance?
The mutual inductance of two coils is said to be one henry if an induced emf of one volt is set up in one coil when the current in the neighboring coil changes at the rate of 1 ampere per second.
What is self-inductance?
The change in magnetic flux induces an emf in the coil itself that opposes the change in a current called self-inductance
What are the uses of mutual inductance?
Some uses of mutual inductance are:
1). Metal detectors
2). Generators
3). Transformer
4). Radio receiver (for generating high-frequency current)