Self-inductance is usually just called inductance. From the knowledge of inductance, we know that whenever the current change occurs, it induces an EMF in the conductor such that it opposes the change in the current. From Lenz’s law, the induced voltage by the changing current has the effect of resisting the change in current, and the voltage is called back-EMF.
In this article, we will talk about self-inductance, definition, formula, units, and dimensions. So let’s get started…
What is self-inductance?
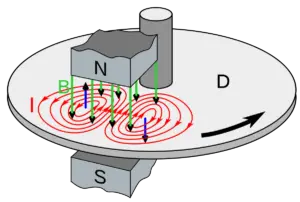
Self-inductance is a phenomenon by which a changing electric current produces an induced emf across the coil itself.
Self-inductance is the property of the current-carrying coil that resists or opposes the change in current flowing through it. This happens mainly due to the self-induced emf generated in the coil itself. In simplified terms, one can also say that self-inductance is a phenomenon in which a voltage is induced in a current-carrying wire. The self-induced emf present in the coil resists the current rise when the current increases and also resists the current fall when the current decreases.
Essentially, the direction of the induced emf is opposite to the applied voltage when the current is increasing, and the direction of the induced emf is in the same direction as the applied voltage when the current is decreasing. The above property of the coil only exists for alternating current, which is alternating current, and not for direct or constant current. Self-inductance always opposes the changing current and is measured in Henry (SI unit).
The induced current always opposes the change in current in the circuit, whether the change in current is an increase or a decrease. Self-induction is a type of electromagnetic induction.
Read Also
Self-inductance formula
Self-inductance is the ratio of the induced electromotive force (EMF) across a coil to the rate of change of electric current through the coil. We denote the coefficient of the self-induction by the letter $L$ in English. Its unit is Henry (H), and EMF (E) is proportional to the rate of change of current, we can write, $$\begin{gathered} E \propto \frac{\mathrm{d} i}{\mathrm{~d} t} \Rightarrow E=L \frac{\mathrm{d} i}{\mathrm{~d} t} \\ \Rightarrow L=\frac{E}{\frac{\mathrm{d} i}{\mathrm{~d} t}}=\text { self inductance }\end{gathered}$$ But the original equation is $$E=-L \frac{\mathrm{d} i}{\mathrm{~d} t}$$ Here, (-) negative sign is because, According to the Lenz’s law the induced emf is in the direction that opposes the rate of change of current.
Coefficient of self-inductance
At any instant, the magnetic flux $\phi$ linked with the coil is proportional to the current $I$ through it, i.e. $$\phi=I$$ $$\text{Or} \qquad \phi=LI\qquad…… (1)$$
Where $L$ is constant for the given coil and is called self-inductance or, more often simply inductance. It is also called the coefficient of self-inductance of the coil. Any change in current sets up an induced emf in the coil given by $$\mathcal{E}=-\frac{d\phi}{dt}=-L\frac{dI}{dt}\qquad…. (2)$$ If in the equation (1), $I=1$, then $\phi=L$.
Thus, the self-inductance of a coil is numerically equal to the magnetic flux linked with the coil when a unit current flows through it.
Again from the equation (2), if $\frac{dI}{dt}=1$, then $\mathcal{E}=-L$
Thus, the self-inductance of a coil may be defined as the induced emf set up the coil due to the unit rate of change of the current through it.
Read Also
- Electromagnetic induction | definition, applications, and history
- What are eddy currents? definition, causes, applications
Units of self-inductance
In the SI system, the unit of self-inductance is Henry (H). From equation (2)
| $$L=\frac{\mathcal{E}}{\frac{dI}{dt}}$$ $$\therefore \text{SI unit of L}=\frac{1V}{1As^{-1}}=1VsA^{-1}=1 \text{Henry}(H)$$ |
The self-inductance of a coil is said to be one henry if an induced emf of one volt is set up in it when the current in it changes at the rate of one ampere per second.
From equation (1), one can note that self-inductance is the ratio of magnetic flux and current. So its SI unit is $weber\; per \;ampere$. Hence $$1VsA^{-1}=1{Wb} A^{-1}=1\text{Henry}(H)$$
Dimensions of self-inductance
We know that
| $$L=\frac{\phi}{I}=\frac{BA}{I}=\frac{F}{qv\sin\theta}.\frac{A}{I},\qquad[\therefore\; F=qv\sin\theta]$$ |
$\therefore$ Dimensions of L
| $$=\frac{MLT^{-2}.L^2}{C.LT^{-1}.A}=\frac{ML^{2}T^{-2}}{A.A}=[ML^{2}T^{-2}A^{-2}]$$ |
Experiment to demonstrate self-inductance
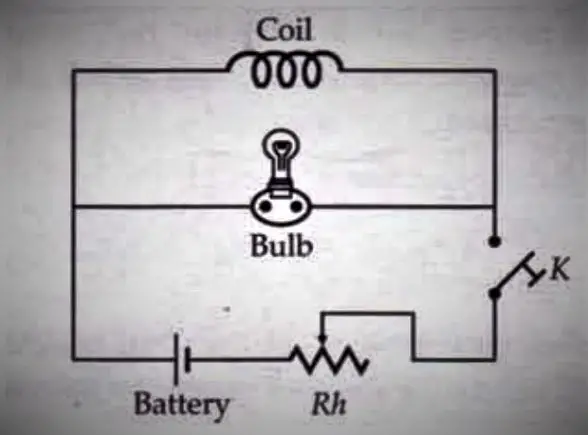
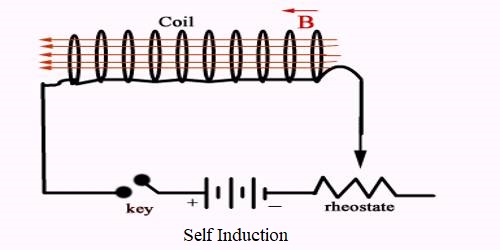
Consider a solenoid that has a large number of turns of insulated wire wrapped around a soft iron core. Such a solenoid is called a choke coil. Connect the solenoid in series with a battery, rheostat, and tapping switch. Connect a bulb in parallel with the solenoid. Press the tapping switch and use the rheostat to adjust the current so that the light bulb glows dimly.
When the switch is released, the bulb will glow brightly for a moment and then go out. Because when the circuit is suddenly broken, the magnetic flux associated with the coil suddenly disappears, that is, the rate of change of the magnetic flux associated with the coil is very large. This creates the largely self-induced emf and current in the coil, causing the bulb to glow brighter for a moment.
Read Also
- Lenz’s law – statement, formula, application, and experiments
- Solenoid, definition, working principle, types, and applications
Factors affecting self-inductance
Factors on which self-inductance depends, Obviously, the self-inductance of a solenoid depends on its geometry and the magnetic permeability of the core material.
- The number of turns. The larger the number of turns in the solenoid, the larger its self-inductance. $$ L \propto N^{2} $$
- Area of the cross-section. The larger the area of the crosssection of the solenoid, the larger its self-inductance. $$L \propto A$$
- Permeability of the core material. The self-inductance of a solenoid increases $\mu_{r}$ times if it is wound over an iron core of relative permeability $\mu_{r}$.
Uses of Self-inductance
The main function of an inductor is to store electrical energy in the form of a magnetic field. Inductors are used below:
- Tuning circuits
- Sensors
- Energy storing device
- Induction motors
- Transformers
- Filters
- Chokes
- Ferrite beads
- Used as relays
Frequently Asked Questions – FAQs
What is self-inductance?
Self-inductance is the property of the current-carrying coil that resists or opposes the change in current flowing through it. This happens mainly due to the self-induced emf generated in the coil itself.
What are the factors upon which the self-inductance of the coil depends?
The self-inductance of the coil depends upon its length, number of turns, area of cross-section, and the permeability of the material of its core.
What is electromagnetic induction?
The process by which EMF is induced in the electrical conductor by changing the magnetic field linked to the conductor is known as electromagnetic induction
Define 1 Henry.
The self-inductance of a coil is said to be one henry if an induced emf of one volt is set up in it when the current in it changes at the rate of one ampere per second.
Why self induction is called inertia?
The coil’s self-inductance is the property due to which it tends to keep the magnetic flux bound to it and resists any change in flux by inducing current in it. This property of a coil is analogous to mechanical inertia. That is why self-induction the inertia of electricity is called induction.