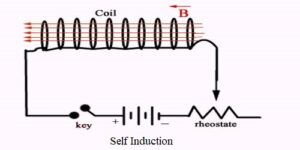
In this short piece of article, we will derive a formula for energy stored in the inductor. So let’s get started…
Formula for energy stored in the inductor derivation
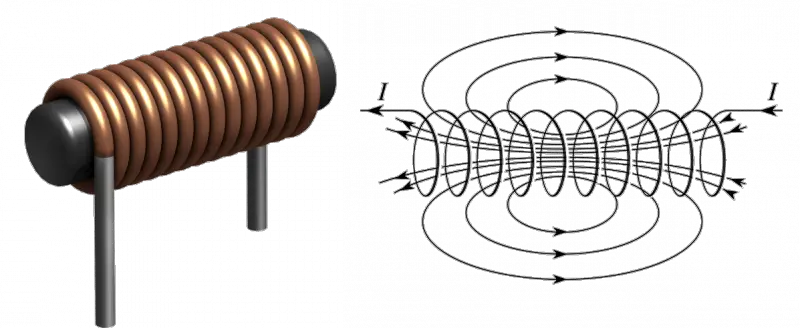
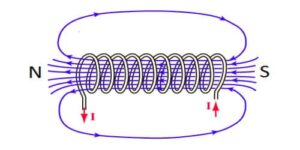
Let’s take an inductor with some inductance, if anyone increases the current through the inductor, in this case, a voltage ${\displaystyle v(t)}$ is induced across the inductor with a polarity that opposes the change in the current.
Read Also
In addition to any voltage drop caused by the inductor’s resistance Charges flowing through the circuit lose potential energy. The external circuit energy needed to overcome this “potential hill” is stored in the increased magnetic field around the inductor. Therefore, an inductor stores energy in its magnetic field. At any instant ${\displaystyle t}$ the power flowing into the magnetic field is ${\displaystyle p(t)}$ which is equal to the rate of change of stored energy ${\displaystyle U}$ is the product of the current ${\displaystyle i(t)}$ and the voltage ${\displaystyle v(t)}$ across the inductor. $${\displaystyle p(t)={\frac {{\text{d}}U} {{\text{d}}t}}=v(t)\,i(t)}\qquad…..(1)$$
From (1) above $${\displaystyle {\begin{aligned}{\frac {{\text{d}}U}{{\text{d}}t}}&=L(i)\,i\,{\frac {{\text{d}}i}{{\text{d}}t}}\\{\text{d}}U&=L(i)\,i\,{\text{d}}i\,\end{aligned}}}$$
When there is no current, there is no magnetic field and the stored energy is zero. Neglecting resistive losses, the energy ${\displaystyle U}$ (measured in joules, in SI) stored by an inductance with a current ${\displaystyle I}$ through it is equal to the amount of work required to establish the current through the inductance from zero, and therefore the magnetic field. This is given by:$${\displaystyle U=\int _{0}^{I}L(i)\,i\,{\text{d}}i\,}$$
If the inductance ${\displaystyle L(i)}$ is constant over the current range, the stored energy is $${\displaystyle {\begin{aligned}U&=L\int _{0}^{I}\,i\,{\text{d}}i\\&={\tfrac {1}{2}}L\,I^{2}\end{aligned}}}$$
Therefore, for a given current, the inductance is also proportional to the energy stored in the magnetic field. This energy is stored as long as the current remains constant. When the current decreases, the magnetic field decreases and induces a voltage in the opposite direction in the conductor, negative at the end where the current enters and positive at the end where it exists. This returns the stored magnetic energy to the external circuit.
Read Also
- Self-inductance of a long solenoid class 12
- Self-inductance | definition, formula, units, and dimensions
When ferromagnetic materials are in close proximity to the conductor, as in an inductor with a magnetic core, the constant inductance equation above only applies to linear regions of magnetic flux at currents below the saturation level of the ferromagnetic material, where the inductance is approximately constant. As the magnetic field in the inductor approaches the level at which the core becomes saturated, the inductance begins to change with current and the integral equation must be used.
Inductor Energy Storage Calculator
Stay tuned with Laws Of Nature for more useful and interesting content.