DERIVATION FOR ELECTRIC POTENTIAL DUE TO AN ELECTRIC DIPOLE

In today’s article we are going to derive an expression for electric potential due to an electric dipole at any point P. Before we starting the derivation let’s take a quick recap about electric dipole.

ELECTRIC DIPOLE

A electric dipole is a pair of opposite point charges with equal magnitude. It is seperated by the very small distance, say 2a. The mid point of location of -q and +q is called the centre of the dipole.

DIPOLE MOMENT

The strength of the electric dipole is measured by a vector quantity called dipole moment. Simply it is denoted as small p. Electric dipole moment is nothing but the product of electric charge q and the seperation distance 2a.
[latexpage]
$$
p=q\times{2a}
$$
It is a vector quantity and it’s direction is always from negative to positive and it’s SI unit is coulomb-meter. Now let’s come on our main article.

DERIVATION FOR ELECTRIC POTENTIAL

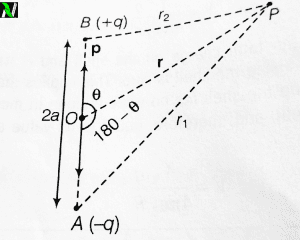
Let’s consider an electric dipole consisting of charges +q and -q seperated by the distance 2a. The dipole moment of this pair of charges is $\displaystyle{|p|=q\times2a}$.

Let O is the centre of the dipole, P be any point near the electric dipole inclined at angle θ as shown in the above figure.
P be the point at which need to find the electric potential. Potential at point P due to -q charge is-
$$
V_1=\frac{-q}{4\pi\epsilon_0r}
$$
And the electric potential at point P due to +q is-
$$
V_2=\frac{+q}{4\pi\epsilon_0r}
$$
As we know that electric potential is related to the work done by the field and it also follows the superposition principle. Therefore total electric potential at point P due to the electric dipole is-
\begin{align}
V_P&=V_1+V_2\\
V_P&=\frac{q}{4\pi\epsilon_0r}\left[\frac{1}{r_2}-\frac{1}{r_1}\right]
\end{align}
Now by the cosine rule-
\begin{align*}
{r_1}^2&=r^2+a^2+2ar\cos\theta\\
{r_2}^2&=r^2+a^2+2ar\cos\left(180^{\circ}-\theta\right)\\
{r_2}^2&=r^2+a^2-2ar\cos\theta\\
\end{align*}
And taking $r^2$ common from above equation
$$
{r_1}^2=r^2\left(1+\frac{a_2}{r_2}+\frac{2a}{r}\cos\theta\right)
$$
If r>>>a, then $\frac{a}{r}$ will be very small.
Therefore, $\frac{a^2}{r_2}$ can be neglected. Now the equation will be-
\begin{align*}
{r_1}^2&=r^2\left(1+\frac{2a}{r}\cos\theta\right)\\
\implies {r_1}&=r\left(1+\frac{2a}{r}\cos\theta\right)^{\frac{1}{2}}
\end{align*}
Taking reciprocal on both side, we get-
$$
\frac{1}{r_1}=\frac{1}{r}\left(1+\frac{2a}{r}\cos\theta\right)^{\frac{-1}{2}}
$$
Similarly for $r_2$
$$
\frac{1}{r_2}=\frac{1}{r}\left(l+\frac{2a}{r}\cos\theta\right)^{\frac{-1}{2}}
$$
Putting these value in equ(1)
$$
\quicklatex{size=11}
V=\frac{q}{4\pi\epsilon_0}\left[\frac{1}{r}\left(1-\frac{2a}{r}\cos\theta\right)^{\frac{-1}{2}}-\frac{1}{r}\left(1+\frac{2a}{r}\cos\theta\right)^{\frac{-1}{2}}\right]
$$
By using binomial theorem $\left[\left(1+x\right)^n=1+nx, x<<<1\right]$ and retaining the terms up to first order in $\displaystyle{\frac{a}{r}}$, we get-
\begin{align*}
V&=\frac{q}{4\pi\epsilon_0r}\left[\left(1+\frac{a}{r}\cos\theta\right)-\left(1-\frac{a}{r}\cos\theta\right)\right]\\
&=\frac{q}{4\pi\epsilon_0r}\left[1+\frac{a}{r}\cos\theta-1+\frac{a}{r}\cos\theta\right]\\
&=\frac{q}{4\pi\epsilon_0r}\left[\frac{2a\cos\theta}{r}\right]\\
&=\frac{q2a\cos\theta}{4\pi\epsilon_0r^2}
\end{align*}
Now the value of electric potential become as follows, where $p=q2a$
$$
\quicklatex{size=18}
\boxed{V=\frac{p\cos\theta}{4\pi\epsilon_0r^2}}
$$
This is the required value of electric potential due to an electric dipole. We see that this potential didn’t depends only on position vector r, but also on the angle between position vector r and the dipole moment p.
The electric potential due to an electric dipole is inversely proportional to the square of the position vector r i.e the distance between the point P from the centre of the dipole.

SPECIAL CASES

By this expression of electric potential, we can find the value of electric potential due to an electric dipole it’s at equatorial line and axial line. Below are

POINT ON THE AXIAL LINE

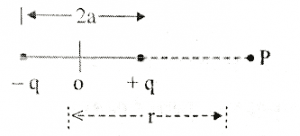
If the point P is on the axial then it must be making angle of 0° or 180° with the electric dipole. If we put angle 0° or 180° in the above expression in place of theta. Then we get the following value.
$$
V=\pm\frac{p}{4\pi\epsilon_0r^2}
$$
Positive sign is used when θ is 0° or if θ is 180° then negative sign will be used.

POINT ON THE EQUATORIAL LINE

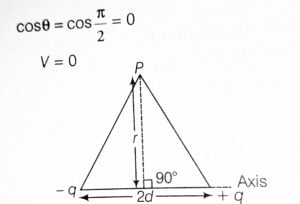
If point is placed on the equatorial line of the electric dipole, then it will be making angle of 90° with the dipole moment. After putting the value of 90° in place of theta in the above equation, we get following expression.
\begin{align*}
\cos\theta&=\cos{180^{\circ}}=0\\
V&=0
\end{align*}
From this expression, we can say that electric potential due to an electric dipole will be zero if point is placed at any point in equatorial line.

FREQUENTLY ASKED QUESTIONS ON DERIVATION OF ELECTRIC POTENTIAL DUE TO AN DIPOLE

1).How do you find the electric potential due to an electric dipole?

Ans- You can find the electric potential due to an electric dipole at any point by this expression.
$$V=\frac{p\cos\theta}{4\pi\epsilon_0r^2}$$
Where p is electric dipole moment and θ is the angle made by the position vector r and electric dipole moment p.

2).What is the electric potential due to electric dipole at an equatorial point?

Ans- Electric potential due to an electric dipole at equatorial point is zero because at equatorial point angle made by position vector of the point P with dipole moment is 90° and value of cos90 is zero.

3).What are the points at which electric potential of a dipole has maximum value?

Ans- Value of electric potential will be maximum when value of cosθ will be maximum and value of cosθ is maximum at 0°. we know that the point on the axial line makes angle 0°. So if point lies on the axial line then it have maximum value.

4).What is the angle of electric dipole moment?

Ans- The angle of electric dipole moment with the axial line is zero. It is because the direction of dipole moment and net electric field in in same direction.

5). What do you mean by electric dipole?

Ans- Electric dipole is nothing but the pair of two opposite charges with very small distance between them.

6). What is an ideal electric dipole?

Ans- Pair of equal and opposite charges seperated by the very small vector distance. If charge q gets larger and distance 2a gets smaller, such that $|p|=q\times{2a}$ remains constant then we got dipole called idea dipole. An ideal dipole having almost zero size.