COMBINATION OF CAPACITORS IN SERIES AND PARALLEL

In this section, we are going to discuss about combination of Capacitors in series and parallel in detail, so stay tuned with us till end.

There are various electrical equipment where Capacitors are used. In some equipment, there can be more than one Capacitor connected. These Capacitors can be connected to each other by parallel or series way.

But more than one Capacitor in single equipment makes equipment heavy in weight and it will be more costly. So sometimes we replace combination of various Capacitors by a single Capacitor.

But how can be we replace combination of Capacitors by a single Capacitor? To do this, we need to know the total capacitance on the Capacitors which we are using in the equipment.

But the question is how can be know this? To know this, we have to learn about the equivalent capacitance. After studying this article, you will able to find the equivalent Capacitance of various Capacitors in series and parallel.

CAPACITOR IN SERIES CONNECTION

What is the meaning of series connection? When we talk about series connection, then we are talking about the connection in which anything is connected with each other by end to end.
[latexpage]
Here anything can be Capacitors. When various Capacitors are connected to each other by end to end method then we say that it is connected by series connection. See, figure below:

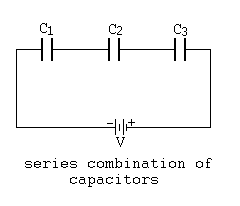
When Capacitors are connected in series then the same electric current is passing through them. If the same electric current is passing, then we can say that they possess same electric charge, let’s say Q.

But they possess different potential difference to its terminal or plates. The total potential difference V is given by the sum of potential difference on each Capacitor.
$$
V=V_1+V_2+V_3
$$
We know the formula of Capacitance of Capacitor is-
$$
C=\frac{Q}{V}
$$
We can rewrite this formula in term of V as follows:
$$
V=\frac{Q}{C}
$$
Similarly;
\begin{align*}
V_1&=\frac{Q}{C_1}\\
V_2&=\frac{Q}{C_2}\\
V_3&=\frac{Q}{C_3}
\end{align*}
Putting this values of $\displaystyle{V_1,V_2, and, V_3}$ in above equation of V, we get the following expression.
$$
V=\frac{Q}{C}=\frac{Q}{C_1}+\frac{Q}{C_2}+\frac{Q}{C_3}
$$
Taking common Q from both side and after cancelling it, we get the final expression, as follows:
$$
\frac{1}{C}=\frac{1}{C_1}+\frac{1}{C_2}+\frac{1}{C_3}
$$
If there are n numbers of Capacitors connected in series then, we can write this formula as-
$$
\frac{1}{C}=\frac{1}{C_1}+\frac{1}{C_2}+\frac{1}{C_3}+…+\frac{1}{C_n}
$$
Where C is called equivalent Capacitance.

CAPACITORS IN PARALLEL CONNECTION

After learning about series connection, now let’s learn about parallel connection of Capacitors. Starting with same question, what is the meaning of parallel connection?

When we talk about parallel connection. Then it’s there is our only one mean that we are talking about the connection in which two or more Capacitors are connected only with two end. In other words, all the positive terminal are joined together and all the negative terminal joined together.

It is not as series connection of Capacitors. In which we connect end to end. See figure below:

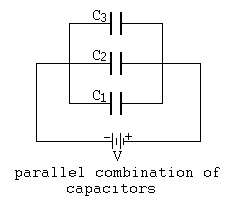
In parallel connection, potential difference at the terminal of each Capacitor are same.

Means potential difference doesn’t change in parallel connection. But electric current get changed. If electric current is different in each Capacitor then there will be different value of electric charges.

The total electric charge is given as the sum of all the electric charges present in all the Capacitors.
$$
Q=Q_1+Q_2+Q_3
$$
From the formula of capacitance, we know that-
$$
C=\frac{Q}{V}
$$
We can rewrite this formula in terms of Q as follows:
$$
Q=CV
$$
Similarly;
\begin{align*}
Q_1&=C_1V\\
Q_2&=C_2V\\
Q_3&=C_3V
\end{align*}
Put this formulae of different Qs in above formula of Q, after putting this formula, we get-
$$
Q=CV=C_1V+C_2V+C_3V
$$
Taking common V from each side and after cancelling, we get-
$$
C=C_1+C_2+C_3
$$
If there are n numbers of Capacitors connected in parallel then, this formula can be written as-
$$
C=C_1+C_2+C_3+…+C_n
$$
Where C is equivalent Capacitance.