EXPRESSION FOR ENERGY STORED IN A CAPACITOR

In this article we are going to derive an expression for energy stored in a capacitor. Want to know the complete derivation process, stay tuned with us till end.

Capacitors are the device which can be used to store electrical energy. It can store electrical energy in the form of electric charges.

When Capacitor are connected to the power supply, the current starts charging the Capacitor, this leads to the accumulation of electric charges on both the plates.

When it disconnected from the power supply, the electric charges starts moving in opposite direction for some interval of time. Due to this property, it acts as a short time rechargeable battery.[latexpage]

DERIVATION PROCESS

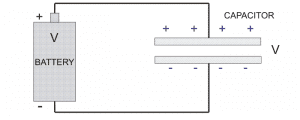
Let’s take a Capacitor having initial charge q, capacitance C and a constant potential difference of V. If q is the electric charge of the capacitor at that instant then ;
$$ q=CV$$
We know that work done is given as W = Vq, which is equivalent to the product of the potential difference and the electric charges.
Hence, if the battery delivers the infinitesimally small amount of charge dq to the capacitor at constant potential V, then-
$$dW=Vdq=\frac{q}{C}dq$$
This work done is stored in the Capacitor as electric potential energy and denoted as dU, so we can write above equation as follows;
$$dU=dW=Vdq=\frac{q}{C}dq$$
Total work done in delivering a charge of amount dq to the capacitor is given by-
$$
U=\int_{0}^{q}\frac{q}{C}dq = \frac{1}{C}\left[\frac{q^2}{2}\right]_{0}^{q} = \frac{1}{2}\frac{q^2}{C}
$$
Therefore, work done is given as-
$$
U=\frac{1}{2}\frac{q^2}{C}
$$
Now, substitute q = CV, we get-
$$
U=\frac{1}{2}CV^2
$$
And after substituting $C=\frac{q}{V}$ we get-
$$
U=\frac{1}{2}qV
$$
This is the required value of electrical energy stored by the Capacitors.

DERIVATION FOR ENERGY DENSITY

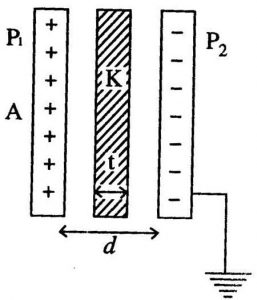
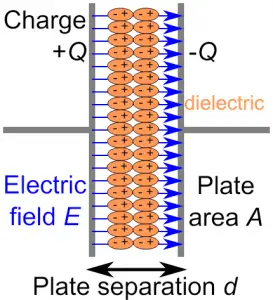
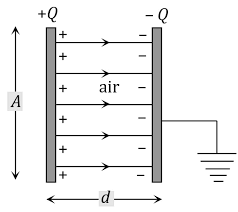
Energy density is the energy stored per unit volume of space in a capacitor. It is denoted by u. If Capacitor have surface area A and seperation distance d then the volume of space is equal to Ad. Thus, the energy density is given as-
\begin{align*}
\text{Energy density}& =\frac{\text{energy stored}}{v}\\
&=\frac{\frac{1}{2}CV^2}{Ad}\\
&=\frac{CV^2}{2Ad}
\end{align*}
Capacitance of the capacitor in term of A is given as-
$$
C=\frac{\epsilon_0A}{d}
$$
Put it into above equation, we get;
\begin{align*}
u&=\frac{1}{2}\frac{\epsilon_0A}{d}\frac{V^2}{Ad}\\
&=\frac{1}{2}\epsilon_0\left(\frac{V}{d}\right)^2
\end{align*}
Put $\frac{V}{d}=E$ in above equation, then we get;
$$
u=\frac{1}{2}\epsilon_0E^2
$$
This is the energy density of charged Capacitor when there is no dielectric medium inserted between the plates.
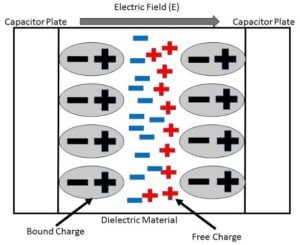
If there is dielectric material inserted between the plates then –
$$
u=\frac{1}{2}\epsilon E^2
$$