Well, In this article, we are going to derive the expression for the capacitance of a parallel plate capacitor when a dielectric slab of thickness t is inserted between the plates. Wants to know all about the derivation, stay tuned with us till the end…

DERIVATION FOR THE CAPACITANCE

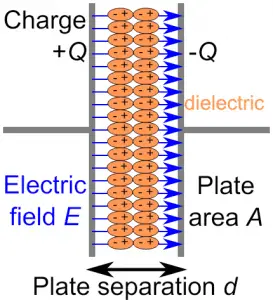
Let’s take a parallel plate capacitor having a plate surface area is A. A dielectric slab of thickness t is inserted between the plates. And the dielectric slab has the dielectric constant K and the permittivity of its medium is ε. See the figure below :

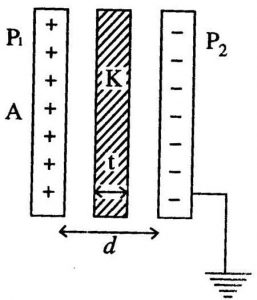
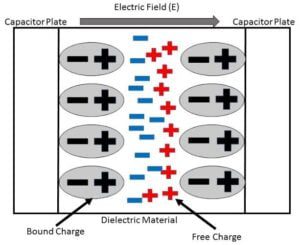
After putting the dielectric slab of thickness t the remaining distance will be (d – t). Let the electric field inside the dielectric slab is E and the field inside the plates and outside the slab is $E_0$.

DERIVATION PROCESS

The electric field inside the slab is given as-
$$
E=\frac{\sigma}{\epsilon}=\frac{\sigma}{K\epsilon_0}=\frac{q}{\epsilon_0KA}
$$
And the electric field outside the slab is given as –
$$
E_0=\frac{\sigma}{\epsilon_0}=\frac{q}{\epsilon_0A}
$$
The total potential difference between the plates is given as the sum of the potential difference due to the slab and without the slab. Which is clearly written below :
\begin{align*}
V&=E_0\left(d-t\right)+Et\\
&=\frac{q\left(d-t\right)}{\epsilon_0A}+\frac{qt}{\epsilon_0KA}\\
&=\frac{Kq\left(d-t\right)+qt}{\epsilon_0KA}\\
&=\frac{Kqd-kqt+qt}{\epsilon_0KA}\\
&=\frac{q\left[kd-kt+t\right]}{\epsilon_0KA}
\end{align*}
Capacitance of any capacitor is given as charge per unit potential difference. Let’s put the value of potential difference in the formula of capacitance.
\begin{align*}
C&=\frac{q}{V}\\
&=\frac{q}{\left(\frac{q\left[kd-kt+t\right]}{\epsilon_0KA}\right)}\\
C&=\frac{\epsilon_0KA}{Kd-kt+t}\\
&=\frac{\epsilon_0KA}{Kd+t\left(1-K\right)}
\end{align*}
This is the required value of capacitance of a parallel plate capacitor when a dielectric slab of thickness t is inserted between the plates.