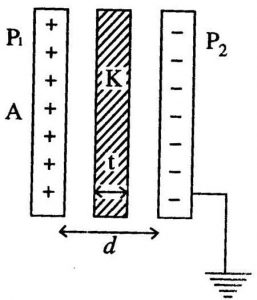
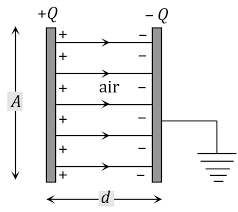
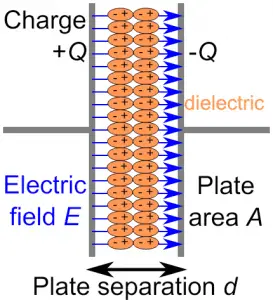
Let’s consider a parallel plate capacitor having plate area A and equal and opposite charges q on both of the plates.
The seperation distance between the plates of the capacitor is d which is much smaller than the plate surface area A.
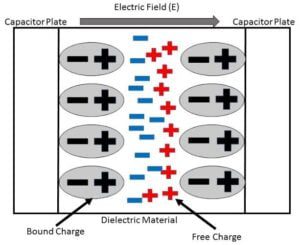
The space between the plates is filled with the material of dielectric constant K and the permittivity of the material medium is ε. See the diagram below.
DERIVATION PROCESS
[latexpage]
First of all let’s find the relationship between the relative permittivity of the medium$\epsilon_r$ and the permittivity of the medium $\epsilon$. The relationship is given as :
$$
\epsilon_r=K=\frac{\epsilon}{\epsilon_0}
$$
From this equation we can write the formula of permittivity of the medium in the form of relative permittivity of the medium also called dielectric constant and the absolute permittivity of the free space. The formula is given as-
$$
\quicklatex{size=20}
\epsilon=\epsilon_r\epsilon_0=K\epsilon_0
$$
Now the electric field between the plates is given as-
\begin{align*}
E&=\frac{\sigma}{\epsilon}\\
&=\frac{\sigma}{K\epsilon_0}\\
\end{align*}
Where the value of $\sigma$ is charge per unit surface area, that is-
$$\sigma=\frac{q}{A}$$ put it in the formula of electric field, which we have obtained above –
$$
E=\frac{q/A}{K\epsilon_0}=\frac{q}{\epsilon_0KA}
$$
Now the relationship between the electric potential difference V and the electric field E is V=Ed. Now after substituting the value of electric field in the formula of electric potential, we get –
$$
V=\frac{qd}{\epsilon_0KA}
$$
Now the capacitance C is given as charge(q) per unit potential difference (V).
\begin{align*}
\quicklatex{size=20}
C&=\frac{q}{V}\\
&=\frac{q}{\left(\frac{qd}{\epsilon_0KA}\right)}\\
C&=\frac{\epsilon_0KA}{d}
\end{align*}
This is the required value of capacitance of a parallel plate capacitor, when a dielectric material is inserted between the plates.
FREQUENTLY ASKED QUESTIONS
1). What is the formula of capacitance of parallel plate capacitor?
Ans– The formula of capacitance of parallel plate capacitor when a dielectric material is inserted between the plates is $$C=\frac{\epsilon_0KA}{d}$$ and when vaccum is filled between the plates then the capacitance is – $$C=\frac{\epsilon_0A}{d}$$
2). What is capacitor derive an expression for capacitance of parallel plate capacitor?
Ans– Capacitor is a passive device which is used to stored electrical charges in electric field.
Go through this article for complete derivation. Expression for capacitance of parallel plate capacitor.
3). What do you mean by parallel plate capacitor?
Ans– A parallel plate capacitor is an arrangement of two metal plates connected in parallel separated from each other by some distance. A dielectric material is filled between the gap of the plates. … This dielectric material does not allow the flow of electric current through it, due to its non-conductive property.