Derive an expression for the capacitance of a parallel plate capacitor class 12

PARALLEL PLATE CAPACITOR

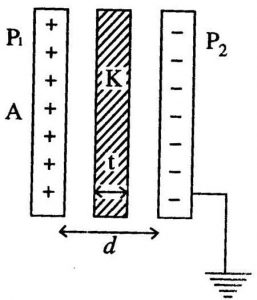
Parallel plate capacitor is a type of Capacitor in which two parallel metal plates having surface area A is held at suitable distance d. One of the plate is insulated and other is earthed. There is vaccum filled between the two conducting plates.

Parallel plate capacitor stored finite amount of electrical energy before dielectric breakdown occurs.

When these both plates are connected to the battery one plate become positively charged and other plate become negatively charged of same magnitude. Due to this a electric field is established between the two plates.

PARALLEL PLATE CAPACITOR CAPACITANCE FORMULA

The direction of the electric field generated between the two plates is in the direction of the motion of electric currents i.e the motion of positive charge.

Every Capacitor has its own Capacitance. Capacitance is the Capacity of the Capacitor to holding electrical charges. We know that parallel plate capacitor is the arrangement of two parallel plates of surface area A and the seperation distance of d.
[latexpage]
The formula for the capacitance of parallel plate capacitor is given as-
$$C=\frac{\epsilon_{0}A}{d}$$

DERIVATION FOR THE EXPRESSION OF CAPACITANCE

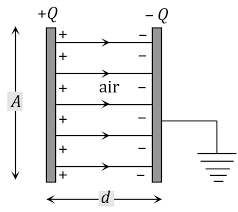
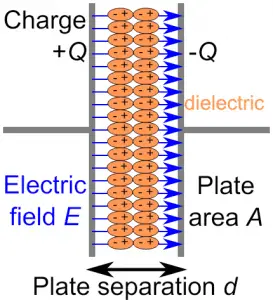
See the above diagram, this is the basic design of a parallel plate capacitor. Here, you can see the two conducting plates  having +Q charge and – Q charge in parallel alignment. These two plate is seperated by the small distance d.

Suppose, +Q charge is given to the first plate and due to charging by induction  -Q charge developed on the inner surface of the second plate and +Q charge is developed on the outer surface of that second plate.

But we have to remove +Q charge from the outer surface of the second plate. So we earthed the outer surface of the second plate. This make second plate completely negatively charged. Due to plate is equal and oppositivly charged a electric field region is established between the plates.

Suppose, the surface charged density of each plate is $\sigma$, then the value of electric field intensity at a point between the two parallel plane sheets of equal and opposite charges is $\frac{\sigma}{\epsilon_{0}}$, where $\epsilon_{0}$ is the permittivity of the free space.

Thus, the electric field intensity between the two plates is given by-
$$E=\frac{\sigma}{\epsilon_{0}}$$
Since, Q is the charge on each plate and A is surface area of each plate then the surface charge density is given as-
\begin{equation}
\sigma=\frac{Q}{A},\ \text{and so}\ E=\frac{Q}{\epsilon_{0}A}
\end{equation}
Now, lets the potential difference between the two plates is V volts, then the electric field between the two plates is given by-
\begin{equation}
E=\frac{V}{d}, \text{or}\ V=Ed
\end{equation}
Now, substitute the value of E from equ(1) to equ(2).
$$
V=\frac{Qd}{\epsilon_{0}A}
$$
Therefore, the capacitance of the capacitor is given as-
\begin{align*}
C&=\frac{Q}{V}=\frac{Q}{\frac{Qd}{\epsilon_{0}A}}\\
C&=\frac{\epsilon_{0}A}{d}
\end{align*}
Where $\epsilon_{0}=8.85\times 10^{-12}$ farad/metre.

We can conclude from this expression that if we want to obtain high capacitance, then  –

• Surface area A of the plates should be taken large.
• d should be taken small i.e plates should be kept close to each other.