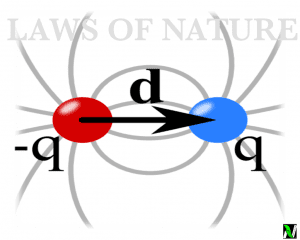
When we are talking about electricity, it means that we are talking about moving charges. We know that electric current is generated when electric charges move, and the production of electric current on a large scale is called electricity.
Electric Charges are the basic units of electricity and magnetism. We know that as charges repel but unlike charges attract each other. This repulsion and attraction is a kind of force, which is exerted by the electric Charges. And the first mathematical calculations of this electrostatic force is done by the French physicist Charles Augustin de coulomb in 1785. And then after this electrostatic force is named Coulomb’s Law in the honor of this physicist.

But the question is – How do charges exert electrical force on the other charges? If we want to understand the force mechanism of charges, then we have to think from the root level. So come on, and let’s start thinking from scratch…
Electric field and force mechanism
Charge can’t exist without mass, which means mass is necessary for the existence of charge. Every charged particle creates a three-dimensional spherical region around them in which if any other charge particle came then it experiences an electrostatic force. It means this electrostatic force is acting on the other charge particle because of the three-dimensionally regions. But what is that three-dimensionally region?
This three-dimensionally region is called the electric field. And the strength of this electric field region starts decreasing as we go away from the charge. So every charged particle has its own three dimensionally spherical coverage area in which any charged particle enters and then starts exerting force.
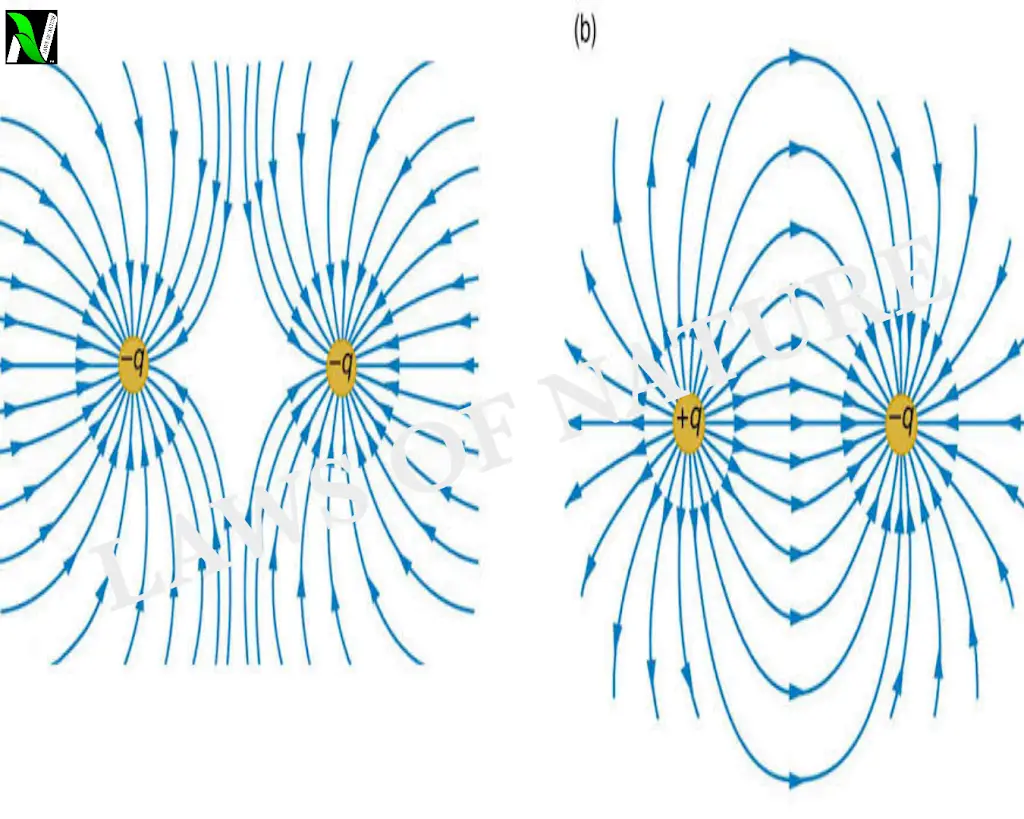
When we bring two charges close to each other then their electric field region starts interacting with each other and this interaction exerts force.
Electric field intensity
Electric field intensity is the mathematical calculation of the strength of the electric field. It is defined as – force $(F)$ experienced by the unit positive charge $(q_0)$ in any electric field $(E)$.
Mathematically, it is given as –
$$E = \frac{F}{q_0}$$
The strength of the electric field intensity decreases with $\frac{1}{r^2}$ as we go away from the source point charge. It means the value of the electric field is different for the different positions of test charges.
Electric field intensity is a vector quantity and its SI unit is $NC^{-1}$.
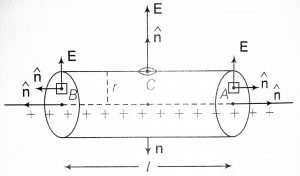
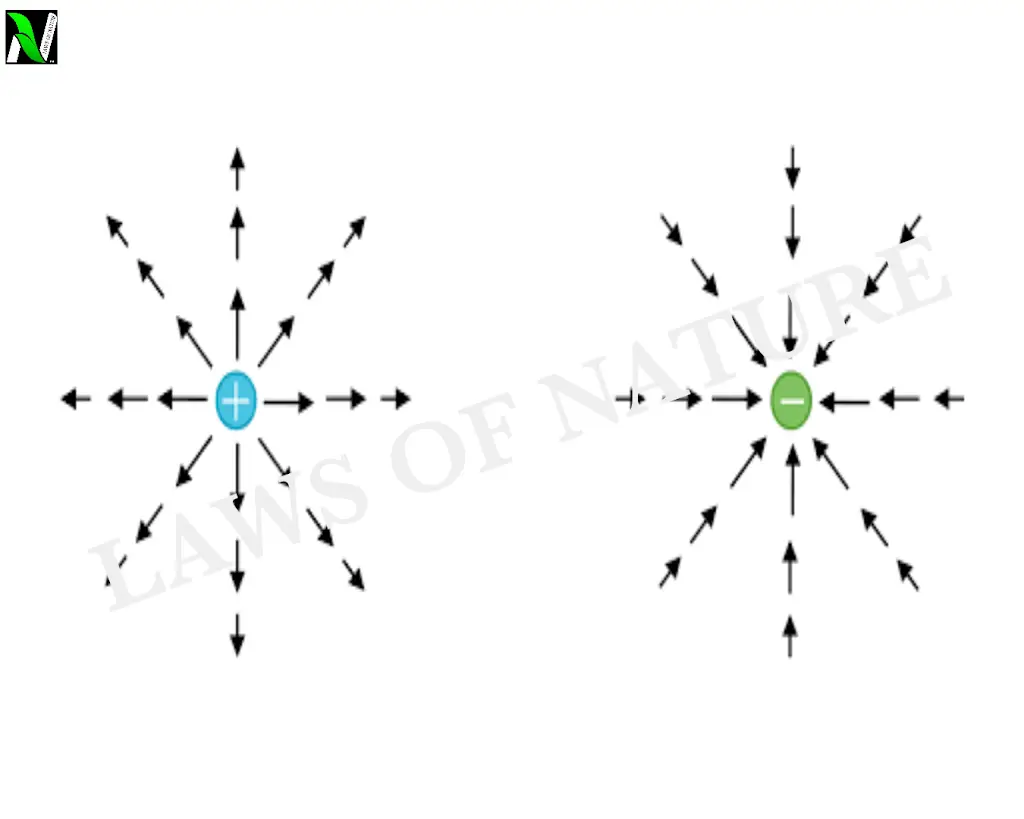
For positive charges, the electric field vector is radially outward. i.e away from the source charge. And for the negative charges, the electric field vector is radially inward, i.e towards the negative source charge. As you can see in the following figure.
Electric field due to a point charge
In this section, we will find the electric field between the two charge system. Let’s take a charge $(q)$ as a source charge and take a charge $(q_0)$ as a test charge, both are separated by the distance $r$. As you can see.
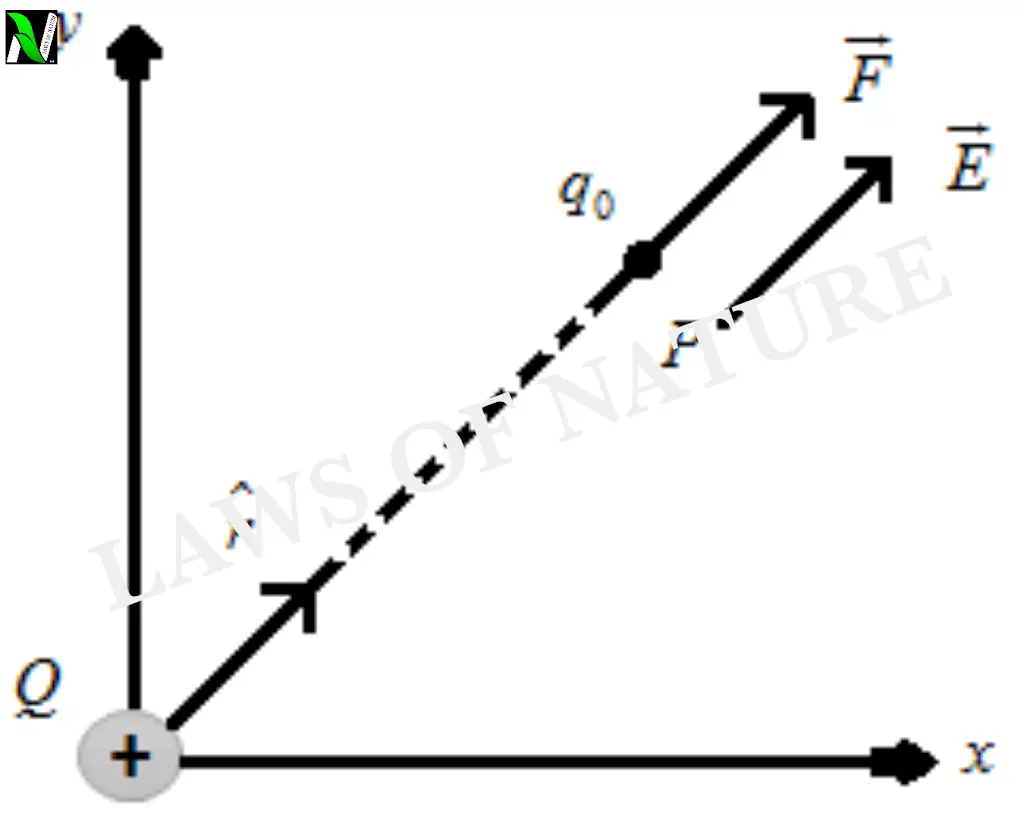
According to Coulomb’s Law, both charges are exerting force on each other and the magnitude of the force is given by – $$F = \frac{q q_0}{4\pi\epsilon_0 r^2}\qquad….(1)$$ And from the equation of electric field intensity, we know that – $$E = \frac{F}{q_0}\qquad…..(2)$$ Put the value of force in equation (2), and we get – $$E= \frac{q q_0}{4\pi\epsilon_0 q_0 r^2}$$ Or $$E= \frac{q}{4\pi\epsilon_0 r^2}$$ This is the required value of electric field at distance $r$ from the source charge $q$.
Watch this video for more reference
Stay tuned with Laws Of Nature for more useful and interesting content.