WHAT IS ELECTRIC FIELD INTENSITY OF AN ELECTRIC DIPOLE?
Electric field intensity of an electric dipole is the three dimensional space around the dipole in which electric effect of the dipole is experienced.
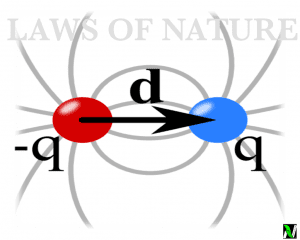
A electric dipole is a pair of point charges with equal magnitude and opposite charges and which is seperated by the small distance d. As you can see in the following figure.
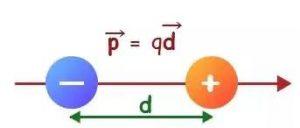
According to the superposition principle the total electric field due to an electric dipole at any point in the three dimensional space is the the vector sum of all the electric field due to the individual charges.
In this article we are going to derive the expression for electric field intensity due to electric dipole in two ways. First when the point is at axial line and second is when the point is at the equatorial line.
POINT AT THE AXIAL LINE
Let’s consider a small dipole of charges +q (point A) and -q (point B), which is seperated by the distance 2l. Where O is the centre of the dipole. The point P (where electric field intensity is to be obtained) is placed on the line which is produced BA to point P i.e axial line at distance r from the centre of the dipole, See figure below:
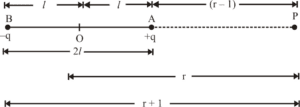
DERIVATION FOR ELECTRIC FIELD AT AXIAL LINE
[latexpage]
Electric field E at point P is given as
\[
\vec{E} = \vec{E_A}+\vec{E_B}
\]
\begin{equation}
|\vec{E_A}| = \frac{1}{4\pi\epsilon_0}\frac{q}{\left(r-l\right)^2}
\end{equation}
\begin{equation}
|\vec{E_B}| = \frac{1}{4\pi\epsilon_0}\frac{q}{\left(r+l\right)^2}
\end{equation}
From the above figure it is clear that $\vec{E_A}>\vec{E_B}$ and also in opposite directions. \[E = |\vec{E}| = |\vec{E_A}-\vec{E_B}|\]
\begin{equation}
E = \frac{1}{4\pi\epsilon_0}\left[\frac{q}{\left(r-l\right)^2}-\frac{q}{\left(r+l\right)^2}\right]\end{equation}\begin{equation}
E = \frac{1}{4\pi\epsilon_0}\left[\frac{q.4rl}{\left(r^2-l^2\right)^2}\right]\end{equation}
\begin{equation}
E = \frac{1}{4\pi\epsilon_0}\left[\frac{2pr}{\left(r^2-l^2\right)^2}\right]\end{equation}
When r >>> l, then
\begin{equation}
E_{axial} = \frac{1}{4\pi\epsilon_0}\frac{2p}{r^3}\end{equation}
This is the required electric field at point P due to an electric dipole on the axial line.
POINT AT THE EQUATORIAL LINE
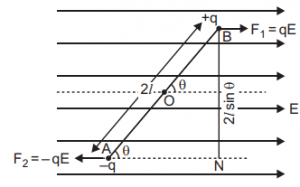
Let’s consider a small dipole having +q charge at point A and -q at point B and the seperation distance between these two charges is 2l. O is the centre of the dipole and the point P (where electric field intensity is to be obtained) is placed at the distance r from the centre of the dipole at the equatorial line. See figure below :
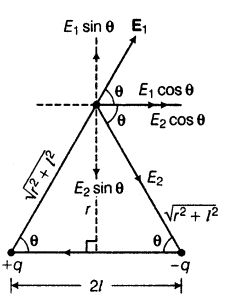
DERIVATIONS FOR ELECTRIC FIELD INTENSITY AT EQUATORIAL LINE
Electric field intensity at point P due to +q charge is –
[latexpage]
\begin{align}
E_1&=\frac{1}{4\pi\epsilon_0}\frac{q}{\left[\sqrt{\left(r^2+l^2\right)}\right]^2}\\
&=\frac{1}{4\pi\epsilon_0}\frac{q}{\left(r^2+l^2\right)},\text{along AP}
\end{align}
Electric field intensity at point P due to -q charge is –
\[
{E_2} = \frac{1}{4\pi\epsilon_0}\frac{q}{\left(r^2+l^2\right)}\;along\;PB
\]
On resolving the equation $E_1$ and $E_2$ in rectangular components. The vector $E_1\sin\theta$ and $E_2\sin\theta$ are equal in magnitude and opposite to each other, and hence cancels each other.
But the vector $E_1\cos\theta$ and the vector $E_2\cos\theta$ are acting on the same direction and hence adds up.
$$
E = E_1\cos\theta + E_2\cos\theta
$$
Here $E_1$ and $E_2$ are equal in magnitude. So resultant electric field intensity become –
\begin{equation}
{E} = 2{E_1}\cos\theta
\end{equation}
The value of cosθ from the figure is given as –
$$
\cos\theta = \frac{l}{\sqrt{r^2+l^2}}
$$
Put the value of cosθ in equation 8, and after putting the equation, we get as follows –
\begin{equation}
E = \frac{2}{4\pi\epsilon_0}\frac{q}{\left(r^2+l^2\right)}\frac{l}{\sqrt{r^2+l^2}}
\end{equation}
Now the formula of electric field intensity become –
\begin{equation}
E = \frac{1}{4\pi\epsilon_0}\frac{2ql}{\left(r^2+l^2\right)^{\frac{3}{2}}}
\end{equation}
But the term 2ql is the dipole moment (p) because |p| = q×2l
\begin{equation}
E = \frac{1}{4\pi\epsilon_0}\frac{p}{\left(r^2+l^2\right)^{\frac{3}{2}}}
\end{equation}
If r >>>> l then,
\begin{equation}
E_{equatorial} = \frac{1}{4\pi\epsilon_0}\frac{p}{r^3}
\end{equation}
This is the required electric field at point P due to an electric dipole on the equatorial line.
From eqs. (12) and (6), we get –
$$
\frac{E_{axial}}{E_{equatorial}} = 2
$$
From the knowledge of this Derivations, we can conclude that both the magnitude and direction of electric field due to the dipole is not only depends on r but also on the angle between position vector r and dipole moment p.
Electric field intensity due to a small dipole is inversely proportional to the cube of the position vector r. It means the value of E is greater, when r is small and it’s value of E is smaller if r greater.
$$ \left(\propto\frac{1}{r^3}\right)$$
But note that electric field intensity due to a single charge is inversely proportional to the square of the position vector r.
$$ \left(\propto\frac{1}{r^2}\right)$$