The motion of charged particles in a uniform magnetic field
In this section, we are going to discuss the motion of charged particles in a uniform magnetic field. We will discuss that what happened to the charged particles when they entered into the region of a uniform magnetic field.
How magnetic field region interact with the charged particles? What behavior or which types of motion is shown by the charged particles if their velocity is parallel or perpendicular to the magnetic field.
In this article we will find out the answers to all these questions, so let’s get started…
If the motion of the charged particles is parallel to the magnetic field
There are various orientations through which a charged particle can enter into a uniform magnetic field. But what if they entered into the magnetic field such that its velocity is parallel to the magnetic field.
Constant velocity produces straight-line motion
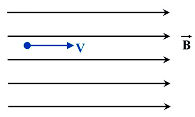
If any charged particles entered into the magnetic field such that their velocity is parallel to the magnetic field then there is no net force act on the particles so they move in straight-line motion.
Recall, Newton’s first law of motion. What do Newton’s first laws of motion state? It states that- An object remains in motion or stationary until and unless an external force acts on them.
This means, if an object experiences no net force, then its velocity will be constant. The object is either at rest (if its velocity is zero), or it moves in a straight line with constant speed (if its velocity is nonzero).
Instead, there are also many cases in which a particle experiences no net force. It may be that the particle exists in a vacuum away from massive bodies (which exert gravitational forces) and electromagnetic fields. Or there could be two or more forces on the particle that are so balanced that the net force is zero. This is the case, for example, with a particle suspended in an electric field, the electric force of which exactly counteracts the force of gravity.
If the resultant force acting on the particle is zero, then according to Newton’s second law, the acceleration must be zero (F = ma). If the acceleration is zero, any velocity of the particle will be maintained indefinitely (or until the resultant force is zero) Since the velocity is a vector, the direction and velocity remain the same, so the particles only move in one direction that is on a straight line. [latexpage]
Charged particles moving parallel to the magnetic field
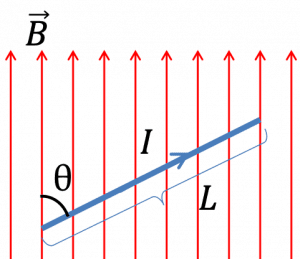
Any charged particles moving in the magnetic field experience magnetic force depends on the angle between the velocity vector v and the magnetic field vector B. Recall, the formula of magnetic force.
$$F=qvB\sin\theta$$
When the magnetic field and the velocity are parallel (or anti-parallel), then the value of sinθ will be zero and there is no force on the particle. In this case, even in a strong magnetic field, the charged particles can move in a straight line. If the angle is between 0 and 90 degrees, the component v parallel to B remains unchanged.
If the velocity of the particles is perpendicular to the magnetic field
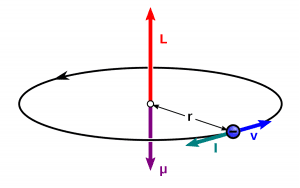
If charged particles enter into the magnetic field such that their velocity is perpendicular to the magnetic field then there will be a magnetic force acted on the charged particles perpendicular to its velocity. Therefore, particles undergo a circular motion.
The circular motion of the charged particles in a uniform magnetic field
The magnetic force causes the charged particles to move in a circular or spiral path. The particle accelerator uses magnetism to keep protons in a circular path. Cosmic rays will spiral when they collide with the magnetic fields of astrophysical objects or planets (the Earth’s magnetic field is an example).
The photo of the bubble chamber in the image below shows the charged particles moving along this curved path. The curved trajectory of charged particles in a magnetic field is the basis of many phenomena and can even be used for analysis, such as in a mass spectrometer. Below shows the path followed by the particles in the bubble chamber.
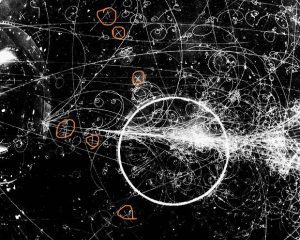
So, if the velocity of the charged particle is perpendicular to the magnetic field then the produced magnetic force will be perpendicular to the velocity of the charged particle. If the magnetic force is perpendicular to the velocity of the charged particle then the work done by the magnetic field on the charged particle will be zero.
Thus, the particle’s kinetic energy and velocity remain constant. The direction of motion of the particle is affected but not its velocity. When a charged particle (q) moves with velocity (v) inside a uniform magnetic field (B), then the magnetic force acting on it is given by-
$$F=q(v\times B)$$
From the right-hand thumb rule, we see that the force $F_m$ is perpendicular to the velocity and hence it changes its path continuously.
This force acts as a centripetal force to the center of the circle and produces a circular motion perpendicular to the magnetic field. If $\mathbf{v}$ and $\mathbf{B}$ are perpendicular to each other, then the particle will describe a circle as shown below:
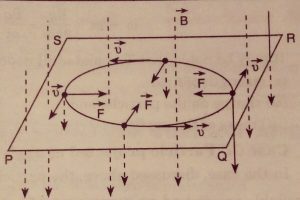
If the charged particle has a component of velocity along $\mathbf{B}$ then the component remains unchanged as the motion along the magnetic field and good thing is that it doesn’t affect by the magnetic field itself.
As centripetal force is required for circular motion, provided by the magnetic force, so the relation between the centripetal force and magnetic force can be given as-
$$\frac{mv^2}{r}=qvB$$
$$\boxed{r=\frac{mv}{qB}=\frac{p}{qB}}$$
Here, (r) is the radius of gyration, or cyclotron radius is the radius of curvature of the circular path on which charged particle of mass (m) is orbiting with velocity (v) perpendicular to the magnetic field (B). In other words, it is the radius of the circular motion of the charged particle in the presence of the magnetic field. Note that the value of sinθ is 1 because the angle between velocity (v) and magnetic field (B) is 90° so the value of sin90° is 1.
But if the velocity is not perpendicular to the magnetic field, then v is the velocity component perpendicular to the magnetic field. The velocity component parallel to the magnetic field does not change because the magnetic force is zero when the motion is parallel or antiparallel to the magnetic field (i.e, θ is 180 ° or 0°). We will study the uses of this concept in the next section on the helical motion.
If you see the above equation then you will find that the radius of the path of the charged particle is proportional to the momentum (mv) of the particle and it is inversely proportional to the magnitude of the charge (q) and magnetic field (B).
In terms of Kinetic energy (K), above equation can be expressed as-
$$r=\frac{\sqrt{2mK}}{qB}$$
$$\therefore\quad p=\sqrt{2mK}$$
Time period (T) of the motion is given by-
$$T=\frac{2\pi r}{v}=\frac{2\pi}{v}\times\frac{mv}{qB}$$
$$or\quad \boxed{T=\frac{2\pi m}{qB}}$$
Angular frequency of the motion is-
$$\omega =\frac{2\pi}{T}\quad or\quad \omega=\frac{qB}{m}$$
$$v_{c}=\frac{qB}{2\pi m}$$
$$\displaystyle{\boxed{\therefore\quad \omega=2\pi v_{c}}}$$
Angular speed of the particle is-
$$\omega=\frac{v}{r}\quad or\quad \omega=\frac{qB}{m}$$
Here, omega (ω) is the angular frequency of the particle moving along the circular path but it is also called cyclotron frequency.
Particles that perform circular motion due to a uniform magnetic field are called cyclotron resonance. The term derives from the name of a cyclic particle accelerator called a cyclotron. The term cyclotron frequency or gyro-frequency is the number of times does a particle moves on the circular path per second.
If the velocity of the particles is not perpendicular to the magnetic field
So, we have recently talked that what would happen if particles entered into the magnetic field such that their velocity is parallel and perpendicular to the magnetic field.
But what would happen if particles entered into the magnetic field such that its velocity is not perpendicular to the magnetic field. In the section on circular motion, we described the motion of a charged particle that is moving in combined circular as well as straight-line i.e helical motion.
The helical motion of the charged particles in a uniform magnetic field
If the velocity is not perpendicular to the magnetic field, then we compare each component of the velocity separately with the magnetic field. We know that the component of the velocity which is perpendicular to the magnetic field produces a magnetic force that is perpendicular to both the velocity and the magnetic field.
$$v_{\perp}=v\sin\theta$$
But the component of the velocity parallel to the magnetic field creates constant straight-line motion along the same direction as the magnetic field.
$$v_{\parallel}=v\cos\theta$$
Where θ is the angle between the velocity and magnetic field. When the particles move circular as well as straight-line then it follows a spiral or helix trajectory and hence, it results in a helical motion. See figure below:
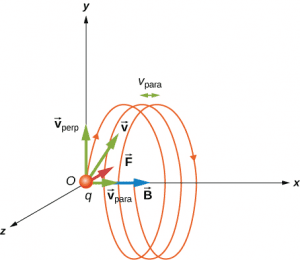
In the above figure, the charged particle is not moving in the same direction as the magnetic field moving. The velocity component perpendicular to the magnetic field creates a circular motion, whereas the component of the velocity parallel to the magnetic field moves the particle along a straight line.
Whenever the particles move in helical motion then there are always some gaps between two consecutive circles. The horizontal distance between the two consecutive circles is called pitch. Thus, the pitch of a helix is given as-
$$P=v_{\parallel}T$$
$$P=\frac{2\pi m v_{\parallel}}{qB}$$
Magnetic mirror
So, we have seen that the charged particle travels in a helical path when the velocity of the charged particle is not perpendicular to the magnetic field.
But sometimes it may enter into the region where the magnetic field is not uniform. For example, suppose a particle travels from a region of a stronger magnetic field to the region of a weaker field, but when it tries to enter into the weaker magnetic field then it returns back to a region of the stronger field. Why?
This is similar to a wave on a string traveling through a very light and thin string but when it strikes a hard wall, it reflects backward (standing waves). If the reflection happens at both ends, the particle is trapped in a so-called magnetic bottle or magnetic mirror.
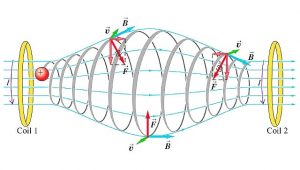
Van Allen Radiation Belts and Aurora Borealis
We have seen that particles may reflect back and get trapped between the two ends if it tries to enter into a stronger magnetic field to a weaker magnetic field or vice versa. But can it happen on a large scale? The answer is yes! It can happen on a large scale.
We know that our earth also produces the magnetic field from the North to the South pole. So, these particles can also be trapped in magnetic fields that are located in the Van Allen radiation belts around the earth, Van Allen belts are part of the earth’s magnetic field.
These belts were first discovered by James Van Allen while trying to measure the flux of the cosmic rays (It is the high-energy particles that are coming on Earth from outside of the solar system) to see whether it resembles the flux measured on Earth.
Van Allen discovered that due to the contribution of particles trapped in the Earth’s magnetic field, the flux on Earth was much greater than in space.
The northern hemisphere Aurora Borealis (Auroras Borealis) are beautiful light shows emitted when ions recombine with electrons that enter into the earth’s atmosphere and they form spiral along the earth’s magnetic field lines (ions are usually oxygen and nitrogen atoms and ionized when they collide with high-energy particles in the earth’s atmosphere). Auroras can also be observed on other planets such as Jupiter and Saturn.
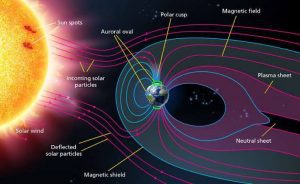
The Van Allen radiation belt around the Earth captures ions produced by cosmic rays entering the Earth’s atmosphere. Spectacular aurora borealis or northern lights gleam over Bear Lake near Elson Air Force Base in Alaska. , This light is produced by luminous oxygen and nitrogen molecules, and ions.
So this is all about the motion of charged particles in a uniform magnetic field. Stay tuned with Laws Of Nature for more useful and interesting content.