ELECTRIC FORCE VS MAGNETIC FORCE

In this article, we are going to understand the basic difference between electric and magnetic forces and we will also compare the effects of the electric and the magnetic fields on the charged particle, so let’s get started…

Whenever you talk about the electric and magnetic forces, you should keep in mind that whether it is an electric force or magnetic force they will influence the motion of charged particles.[latexpage]

However, the resulting change to the charged particles’ trajectory will qualitatively differ for both forces. Below we will briefly review the two types of force and compare their effects on a charged particle.

ELECTROSTATIC FORCE AND MAGNETIC FORCE ON THE CHARGED PARTICLES

IN ELECTROSTATIC

Recall the electrostatic chapter and see what you have learned, if the electric field E is unchanged then the electrostatic force F on any charged particle q is given as-
$$F=qE$$
Where F is the force vector, q is the charge, and E is the electric field vector. Note that the direction of electric force F is identical to electric field E if the charge is positive, but if the charged particle is negative then the direction of electric force is in opposite direction. This electric field may be produced by a larger charge, Q, acting on the smaller charge q over a distance r so that:
$$E=\frac{F}{q}=K|\frac{Qq}{qr^2}|=K|\frac{Q}{r^2}|$$
It should be noted that the electric force F acts parallel to the electric field E. The curl of the electric force will be zero, i.e.
$$\nabla \times E = 0$$
From this, one can conclude that the electric field can work and a charged particle in a pure electric field follows the tangent of an electric field line.

IN MAGNETISM

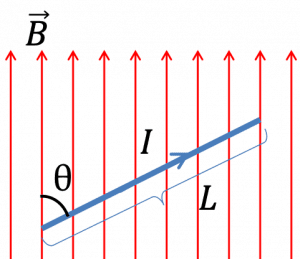
But in contrast to the magnetism, the magnetic force on a charged particle (when it is moving with v velocity) is orthogonal to the magnetic field, and it is given as-
$$F=q(v\times B) =qvB\sin\theta $$
where B is the magnetic field vector, v is the velocity of the particle and θ is the angle between the magnetic field and the particle velocity. The direction of magnetic force can be easily determined by the use of the right-hand rule.

If the particle velocity by any means, aligned parallel to the magnetic field, or it becomes is zero, then the magnetic force will also be zero. This is different from an electric field, where the speed of the particle at any given point in time does not affect the magnitude or direction of the electric force.

The dependency on the angle of the fi magnetic field also causes has the effect that the charged particles move in a circular or helical fashion perpendicular to the magnetic field lines, while a particle in an electric field moves in a straight line along an electric field line.

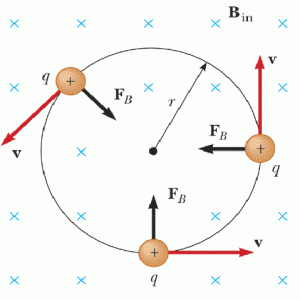
Another difference between the electric and magnetic force is that the work done by the magnetic force on the charged particle is zero because the particle moves in a circular motion and ends up at the same initial point. We can express this mathematically as follows:
$$\oint B\cdot dr=0$$

KEY POINTS BETWEEN ELECTRIC FORCE AND MAGNETIC FORCE

Stay tuned with Laws Of Nature for more interesting and useful content.