Magnetic force on a current-carrying conductor in a uniform magnetic field
We know that when a charged particle moves it creates an electric current and magnetic field as well, and we have seen the related proof in oersted experiment in the previous article. So it is sure that a current-carrying conductor produces a magnetic field around itself in the form of concentric circles.
We also know that when two magnetic fields interact with each other they exert force on each other whether they are like or unlike magnetic fields. Here, like or unlike magnetic field means interaction of N-N or N-S poles of a magnet, in both cases, they exert force on each other.
This means if we place a current-carrying conductor in an external magnetic field then it experiences a magnetic force. In the below figure, you can clearly see that a current-carrying conductor AB is placed in the external magnetic field which is produced by a horseshoe magnet and definitely this conductor is experiencing magnetic force.
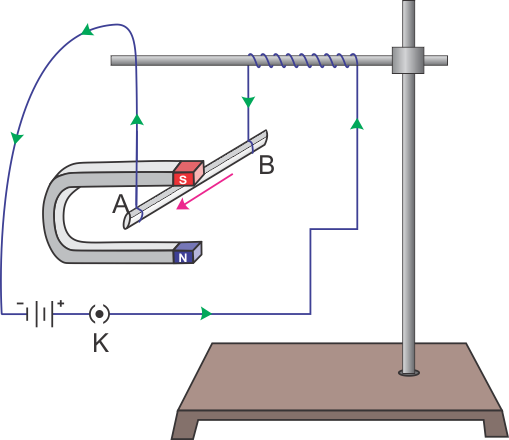
Here, in this present article, we will derive an expression for the magnetic force experienced by the current-carrying conductor in an external magnetic field. So let’s get started…[latexpage]
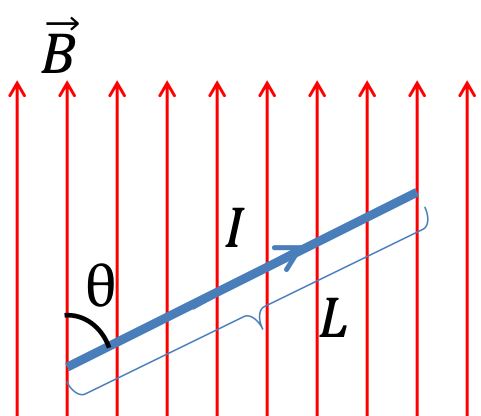
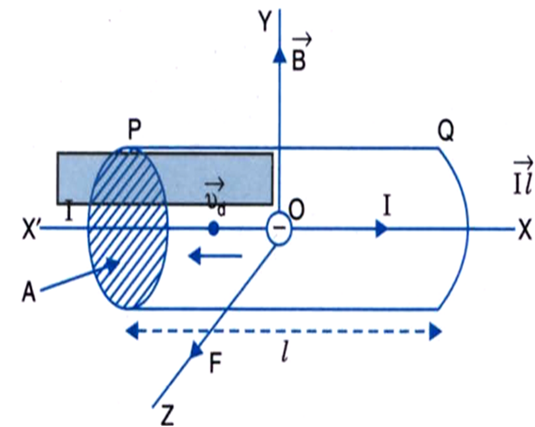
Let’s consider a portion of length $\displaystyle{\mathbf{L}}$ and cross-sectional area $\displaystyle{\mathbf{A}}$ of a straight current-carrying conductor through which current $\displaystyle{\mathbf{I}}$ is flowing. And also, consider a magnetic field $\displaystyle{\mathbf{B}}$ in the plane of the paper directed uniformly upwards making an angle θ with the direction of the velocity of the electrons, see figure above.
Let $\displaystyle{ \mathbf{n}}$ be the numbers of free electrons per unit volume of the conductor and $\displaystyle{ \mathbf{v_d}}$ is the drift velocity of electrons. From the relation, $\displaystyle{F= \mathbf{q}v\times \mathbf {B}}$, where $\displaystyle{\mathbf {q}}$ is the magnitude of the charged particle. Here, in this case $\displaystyle{ \mathbf{e}}$ is the magnitude of the negative charged particle i.e electrons.
So, however the conductor makes an angle θ with the magnetic field $\displaystyle{ \mathbf {B}}$ measured from the conductor towards the field $\displaystyle{ \mathbf {B}}$, then the magnetic force $\displaystyle{ \mathbf {F’}}$ on each electrons is given by- $$\displaystyle{ \mathbf {F’}=ev_d \mathbf {B} \sin\theta}$$ Numbers of electrons in the length $\displaystyle{\mathbf{L}}$ of the conductor is $$N=n \mathbf{A} \mathbf{L}$$ The total magnetic force $\displaystyle{ \mathbf {F}}$ acted on all the free electrons resides in the length $\displaystyle{ \mathbf {L}}$ of the conductors is given as- \begin{equation*}\begin{split}F=F’N&= (ev_d \mathbf {B} \sin\theta)( n \mathbf{A} \mathbf{L})\\&= (ne \mathbf{A} v_d) \mathbf {B} \mathbf{L} \sin\theta \end{split} \end{equation*} As we know that $ \displaystyle {ne \mathbf{A} v_d}$ is nothing but the expression of the electric current. Now from the knowledge of this, expression for the magnetic force can be rewritten as- $$\quicklatex{size=15}\boxed{F=\mathbf{I} \mathbf {B} \mathbf{L} \sin\theta}$$ or $$\quicklatex{size=15}\boxed{F=\mathbf{I}(\mathbf {B}\times \mathbf{L})}$$
Case of minimum force
As we have seen above the magnetic force experienced by the current-carrying conductor is dependent upon the magnitude of the current, magnetic field, and length of the conductor. But there is one more thing on which magnetic force depends and that is the orientation of the conductor in the magnetic field. I mean to say the angle between the magnetic field and the direction of the velocity of the electrons.
If θ = 0° or 180°, then $F=\mathbf{I} \mathbf {B} \mathbf{L} \sin{0} ^{\circ} =0$ because [$\displaystyle{\therefore\;\sin{0}^{\circ}=0\;and\;\sin{180}^{ \circ}=0}$]. It means, if a conductor is placed parallel to the magnetic field then it experience zero magnetic force due to the magnetic field.
Case of maximum force
If the conductor is aligned perpendicularly to the magnetic field, then the force is maximum because the sine value of 90° is 1, i.e $\sin{90} ^{\circ} =1$ $$F_{max} =\mathbf{I} \mathbf {B} \mathbf{L} \sin{90} ^{\circ}= \mathbf{I} \mathbf {B} \mathbf{L}$$ It means, if a current carrying conductor is placed perpendicular in the magnetic field then it experience maximum magnetic force due to magnetic field.
Rules to find out the direction of the magnetic force
The direction of the magnetic force acting on the current-carrying conductor in a magnetic field can be found by any of the following two rules.
Right hand palm rule
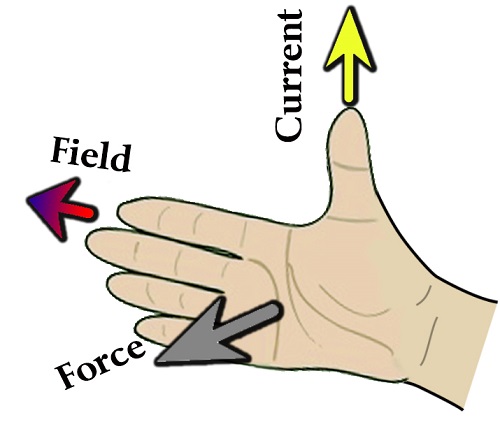
According to this rule, if we stretch our right-hand palm such that the thumb points in the direction of the current (I) and the stretched fingers in the direction of the magnetic field (B), then the magnetic force (F) on the conductor will be perpendicular to the palm in the direction of pushing by the palm. See figure below:
Fleming’s left-hand rule
If the forefinger, middle finger, and thumb of the left hand are stretched mutually perpendicular to each other such that the forefinger points in the direction of the magnetic field (B) and the middle finger in the direction of the current (I), then the thumb will automatically point in the direction of the magnetic force (F) on the conductor. See figure below:

Stay tuned with Laws Of Nature for more useful and interesting content.