Here, in this article, we will briefly discuss the different types of cyclotrons. So let’s get started…
Types of cyclotron
Since E.O Lawrence and Livingston created the cyclotron in the years 1929-30, from then many types of cyclotrons have been made or evolved in different forms. Wait, If you didn’t know about the cyclotron or if you forget it then please read about cyclotron first. Some basic types of the cyclotron are given below:
Classic cyclotron
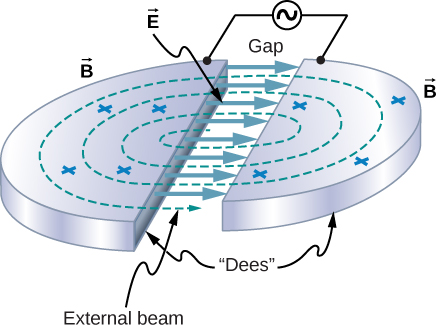
It is the first type of cyclotron invented by E.O Lawrence and Livingston. It has a uniform magnetic field and constant frequency. In this cyclotron, the radiofrequency of the alternating voltage is equal to the particle’s cyclotron resonance frequency, due to this equivalence, the particle completes one revolution per voltage cycle. The radius of the spiral orbit of the charged particle is given as- $$r=\frac{mv}{qB}$$
This cyclotron is strictly limited to the non-relativistic energies, which means it accelerates the charged particle to a velocity that is very slower than the speed of light and doesn’t show a relativistic phenomenon. The particle’s output energy is small compared to the particle’s rest energy and had a focusing problem.
Relativistic effects on the particles in the cyclotron
In the non-relativistic consideration, the frequency of the cyclotron does not depend on the speed of the particle or the radius of the particle’s orbit. As the beam spirals outward, the frequency of revolution remains constant and the beam continues to accelerate as it travels a greater distance in the same time period.
But in contrast to relativistic consideration, as particles approach the speed of light, the cyclotron frequency decreases proportionally to the particle’s Lorentz factor. The mathematical proof of this statement is given below:
Therefore, the acceleration of relativistic particles requires a change to compensate for the relativistic effect as the particles approach to speed of light. If the RF (radio frequency) of the oscillator is varied to compensate for the relativistic effect then it leads to the synchrocyclotron or if the magnetic field is varied during the acceleration that leads to the isochronous cyclotron.
During the acceleration, the relativistic mass of the charged particle can be given as:$${\displaystyle m={\frac {m_{0}}{\sqrt {1-\left({\frac {v}{c}}\right)^{2}}}}={\frac {m_{0}}{\sqrt {1-\beta ^{2}}}}=\gamma {m_{0}}}$$
where ${\displaystyle m_{0}}$ is the rest mass of the charged particles, ${\displaystyle \beta ={\frac {v}{c}}}$ is the relative velocity, and ${\displaystyle \gamma ={\frac {1}{\sqrt {1-\beta ^{2}}}}={\frac {1}{\sqrt {1-\left({\frac {v}{c}}\right)^{2}}}}}$ is the Lorentz factor.
Therefore, relativistic cyclotron frequency and angular frequency can be given as- $$\begin{aligned} f&={\frac {qB}{2\pi \gamma m_{0}}}={\frac {f_{0}}{\gamma }}={f_{0}}{\sqrt {1-\beta ^{2}}}\\&={f_{0}}{\sqrt {1-\left({\frac {v}{c}}\right)^{2}}}\end{aligned}$$ and $$\begin{aligned}\omega &={2\pi f}={\frac {qB}{\gamma m_{0}}}={\frac {\omega {0}}{\gamma }}={\omega {0}}{\sqrt {1-\beta ^{2}}}\\&={\omega _{0}}{\sqrt {1-\left({\frac {v}{c}}\right)^{2}}}\end{aligned}$$ where, ${\displaystyle f_{0}}$ is the cyclotron frequency in classical consideration, and ${\displaystyle \omega _{0}}$ is the cyclotron angular frequency in classical consideration.
The radius of the particle moving in a static magnetic field is- $${\displaystyle r={\frac {v}{\omega }}={\frac {\beta c}{\omega }}={\frac {\gamma \beta m_{0}c}{qB}}}$$ where ${\displaystyle \omega r=v=\beta c}$ and $v$ is the linear velocity of the particle.
Synchrocyclotron

Synchrocyclotron is a variant of the classical cyclotron patented by Edwin McMillan. In which the radio frequency (RF) of the oscillator electric field is varied to compensate for the relativistic effects that risen when particle velocity approaches the speed of light. This is in contrast to the classical cyclotron, where the frequency is held constant. For the acceleration through the synchrocyclotron, the frequency of the charged particle is given as-
$${\displaystyle f={\frac {f_{0}}{\gamma }}={f_{0}}{\sqrt {1-\beta ^{2}}}}$$ where $f_0$ is the classical cyclotron frequency and $\beta=\frac{v}{c}$ is the relative speed of particle w.r.t speed of light.
The major difference between the synchrocyclotron and the classical cyclotron is that, In the synchrocyclotron, only one dee (hollow “D”-shaped metal sheet electrode) is used, while the other pole is open. Furthermore, in a synchrocyclotron, the frequency of the oscillating electric field is decreasing continuously instead of being kept constant so as to maintain cyclotron resonance for relativistic velocities. One terminal of the oscillating electric potential is changing periodically and is applied to the dee and the other terminal is connected to the ground potential. The protons and deuterons are accelerated in circles of increasing radius. The acceleration to the particles takes place when they enter and leave the dees.
Isochronous cyclotron
Isochronous cyclotron is the alternative to the synchrocyclotron. It has a magnetic field that increases with radius, rather than time. Isochronous cyclotrons have the capacity of producing a much greater current beam than synchrocyclotrons, however, they require azimuthal variations of the magnetic field strength in order to achieve a strong focusing effect and to keep trapped particles on their spiral-shaped path. For using azimuthal variations in field strength, an isochronous cyclotron is also called an “AVF (azimuthal varying field) cyclotron.

The focusing solution of the particle was proposed by L. H. Thomas in 1938. Recall the relativistic radius of the particle ${\displaystyle r={\frac {\gamma m_{0}v}{qB}}}$ and the relativistic cyclotron frequency ${\displaystyle f={\frac {f_{0}}{\gamma }}}$, from this one can choose ${\displaystyle B}$ to be proportional to the Lorentz factor, ${\displaystyle B=\gamma B_{0}}$. Substituting value of B in the formula of radius of the particle, then the relation gives ${\displaystyle r={\frac {m_{0}v}{qB_{0}}}}$ which is only dependents on the velocity ${\displaystyle v}$, as like in the non-relativistic case and here, the cyclotron frequency is also constant.
In the isochronous cyclotron, the transverse de-focusing effect of this radial magnetic field is compensated by the ridges on the magnet faces. These ridges also vary the magnetic field azimuthally. This allows the charged particles to be accelerated continuously on every period of the radio frequency, rather than in bursts as occurs in most other accelerator types. The principle in which alternating field gradients have a net focusing effect is called strong focusing.
H− cyclotron
A cyclotron accelerates negative hydrogen ions, making it easier to deflect the beam out of the machine with a positive charge. These are bent in the opposite direction by the magnet so that the beam emerges from the machine.
Stay tuned with Laws Of Nature for more useful and interesting content.