In this short piece of article, we will derive a formula for the Intensity of electromagnetic waves. Going through this article, you will be able to derive the formula for the Intensity of electromagnetic waves by yourself. So, stay tuned with this article.
Intensity of electromagnetic wave formula derivation
The intensity of an electromagnetic wave is defined as the amount of energy passing through a unit area per unit of time.
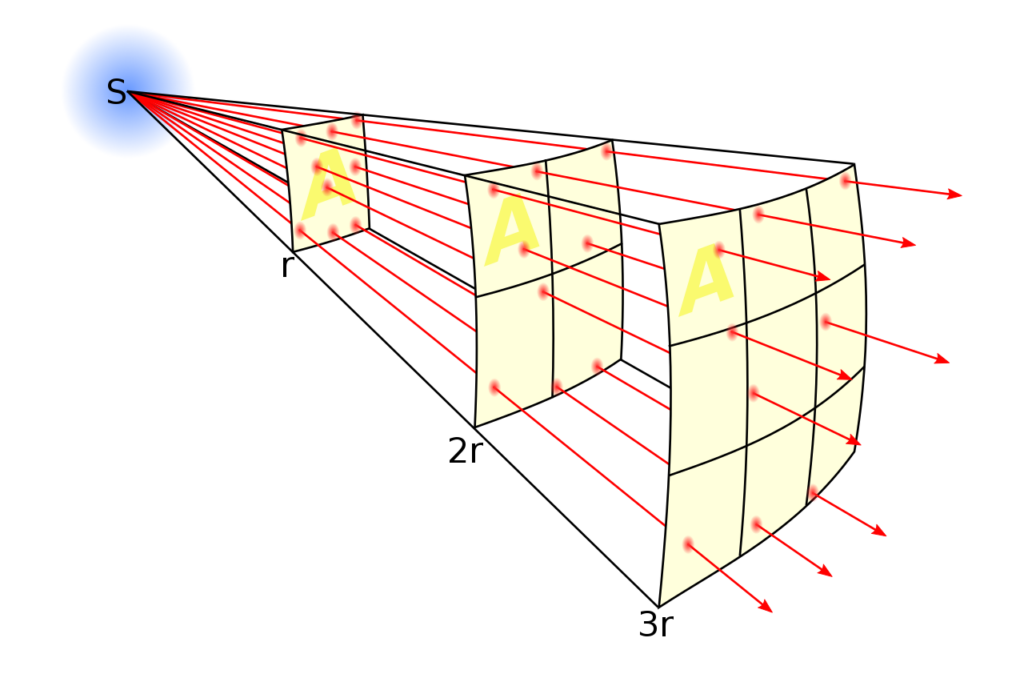
To derive the formula for intensity, we can start with the expression for the energy density of an electromagnetic wave.
The energy density u of an electromagnetic wave is given by:
\begin{equation} u = \frac{\epsilon_0}{2} E^2 + \frac{1}{2\mu_0}B^2 \end{equation}
where E is the electric field, B is the magnetic field, ε0 is the permittivity of free space, and μ0 is the permeability of free space.
The time-averaged power per unit area carried by the wave is given by the Poynting vector, which is defined as:
\begin{equation} \vec{S} = \frac{1}{\mu_0} \vec{E} \times \vec{B} \end{equation}
where the cross product gives the direction of energy flow. The magnitude of the Poynting vector is the intensity I of the wave:
\begin{equation} I = |\vec{S}| = \frac{1}{\mu_0} |\vec{E}| |\vec{B}| \sin \theta \end{equation}
where θ is the angle between the electric and magnetic fields.
For a plane wave, the electric and magnetic fields are perpendicular to each other and to the direction of propagation, so θ is 90 degrees and sin θ is equal to 1. Thus, we have:
\begin{equation} I = \frac{1}{\mu_0} |\vec{E}| |\vec{B}| \end{equation}
Using the relationship between the electric and magnetic fields in a plane wave, namely E = cB, where c is the speed of light, we can simplify this expression to:
\begin{equation} I = \frac{1}{\mu_0 c} E^2 \end{equation}
This is the formula for the intensity of an electromagnetic wave in terms of the electric field strength E. It shows that the intensity is proportional to the square of the electric field amplitude and inversely proportional to the permeability of free space and the speed of light.
Read Also:
- Transformer – Definition, Types, Working Principle, and Constructions
- LC oscillation class 12
- Expression for energy and average power stored in a pure capacitor
- Sources of electromagnetic waves, class 12
- Mathematical representation of electromagnetic waves, class 12
- Maxwell’s prediction of electromagnetic waves, class 12
Frequently Asked Questions – FAQs
What is the formula for the intensity of electromagnetic waves?
The intensity of an electromagnetic wave is a measure of the rate at which energy is transported by the wave per unit area perpendicular to the direction of wave propagation. Mathematically, it is defined as the power per unit area and is given by the formula:
\begin{equation} \text{Intensity} = \frac{\text{Power}}{\text{Area}} \end{equation}
What is the intensity of a wave?
The intensity of an electromagnetic wave is the rate at which energy is transported by the wave per unit area perpendicular to the direction of wave propagation
What is the intensity of electromagnetic waves in terms of the magnetic field?
The intensity of electromagnetic waves in terms of the magnetic field is given as: \begin{equation} I = \frac{1}{\mu_0 } cB^2 \end{equation}
What is the intensity of electromagnetic waves in terms of the electric field?
The intensity of electromagnetic waves in terms of the electric field is given as: \begin{equation} I = \frac{1}{\mu_0 c} E^2 \end{equation}
What is the unit of intensity?
The unit of intensity is watts per square meter (W/m²).
Stay tuned with Laws Of Nature for more useful and interesting content.