In this article we are going to derive a relationship between the electric field and electric potential. So keep reading till end.
RELATIONSHIP BETWEEN ELECTRIC FIELD AND ELECTRIC POTENTIAL
[latexpage]
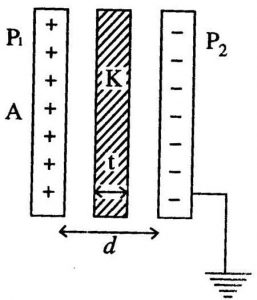
Let’s consider a positive test charge $q_0$ which moves a small distance $d_s$ from one equipotential surface to another equipotential surface.
The test charge $q_0$ is moving such that, it makes an angle θ with the direction of the electric field (E). Suppose, a positive test charge ($q_0$) moves through a differential displacement $d_s$ from one equipotential surface to the adjacent equipotential surface. As shown in following figure.
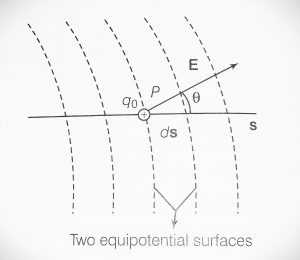
If test charge is moving from one equipotential surface to another equipotential surface then some work done is required to move this charge particle. Without any work done it cannot move.
But as we know that, if this test charge particle moves from one point to another point on the same equipotential surface then there is no any need of work done.
Here the work is done by the electric field on the test charge $q_0$ and the value of work done by the electric field on the test charge is $\displaystyle{-q_0dV}$. This magnitude of work done by the electric field can also be written as scalar product $\displaystyle{\left(q_0E.d_s\right)}$ or $\displaystyle{\left(q_0Ed_s{\cos\theta}\right)}$
Equating these equations of the work done, we get-
\begin{align*}
-q_0dV&=q_0E\left(\cos\theta\right)d_s\\
E\cos\theta&=-{\frac{dV}{d_s}}
\end{align*}
Since, $\displaystyle{E\cos\theta}$ is the components of electric field E in the direction of the displacement $d_s$.
$$
E_s=-{\frac{\partial V}{\partial s}}
$$
If we take the s-axis, in the form of x, y and z-axis, then we can easily find the value of components of E at any point as below.
$$
E_x=-{\frac{\partial V}{\partial x}};E_y=-{\frac{\partial V}{\partial y}};E_z=-{\frac{\partial V}{\partial s}}
$$
For the simple situation when the electric field E is uniform.
$$
\boxed{E=-{\frac{\Delta V}{\Delta s}}}
$$
Here negative sign shows that the direction of electric field is in the direction of decreasing electric potential. We know that $\Delta V$ is negative.
$$
\Delta V=-|\Delta V|
$$
If we can rewrite this equation as follows-
$$
\boxed{|E|=-{\frac{\Delta V}{\Delta s}}+{\frac{|\Delta V|}{\Delta s}}}
$$
Further, the magnitude of electric field is given by the change in the magnitude of electric potential per unit displacement normal to the equipotential surface at the point. This is called potential gradient.
$$
|E|=-{\frac{dV}{dr}}=-\left(\text{potential gradient}\right)
$$
After stating the relationship between electric field and electric potential, we thus arrive at two important conclusion.
1). Electric field is in the direction in which electric potential decreases steepest.
2). Magnitude of electric field is given by the change in the magnitude of electric potential per unit displacement normal to the equipotential surface at the point.