Derivations for electric field intensity due to a uniformly charged ring.

We are going to derive the expression for electric field intensity, due to a uniformly charged thin ring at the point P on its axis which is passing through its centre. So stay tuned with us till end.

DERIVATIONS OF ELECTRIC FIELD INTENSITY DUE TO A UNIFORMLY CHARGED RING

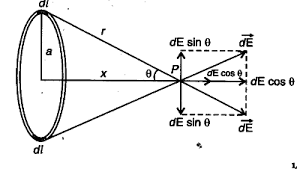
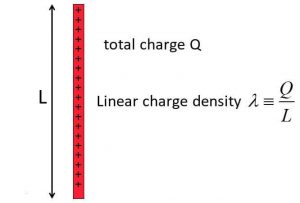
Let’s consider a uniformly charged thin ring of radius a. Let λ is the linear charged density of the ring. Let P is the point on the axis at distance x from the centre of the ring.

Consider a small length element dl of the ring which is at distance r from the point P. Electric charge on this length element dl is dq = λ.dl, If we consider this small length element as a point charge then the electric field intensity at point P due to the small element dl is –
[latexpage]
\begin{equation}
\begin{split}
dE& = \frac{1}{4\pi\epsilon_0}.\frac{dq}{r^2}\\
& = \frac{1}{4\pi\epsilon_0}.\frac{\lambda.dl}{r^2}
\end{split}
\end{equation}
After applying Pythagoras theorem in above right angled triangle, we get $r^2$ = $a^2$ + $x^2$, now the electric field intensity formula becomes as follows –
\begin{equation}
dE = \frac{1}{4\pi\epsilon_0}.\frac{\lambda.dl}{\left(a^2+x^2\right)}
\end{equation}
Where you can clearly see that dE makes an angle $\theta$ with the axis of the ring. After resolving dE in two components, we have :

1). $dE\cos\theta$ is the parallel to the axis.
2). And $dE\sin\theta$ is the perpendicular to the axis.

Till now, we have derived the expression for electric field intensity due to a small length element dl, but is there exists only one small length element dl in the ring, definitely not, there are many such small length element in the ring. Which give rise to the electric field intensity dE at point P having horizontal and vertical electric field components.

All the horizontal components of electric field intensity i.e $dE\cos\theta$ due to the small length element dl are in the same horizontal direction, so all the electric field intensity at point P, added up algebraically. But the vertical components of electric field intensity i.e $dE\sin\theta$ due to the small length element dl get cancelled out with the vertical components of other length element dl because they are equal and opposite.

Therefore, the net electric field intensity due to the charged ring at point P is –
\begin{equation}
E = \Sigma{dE\cos\theta} = \int_{whole\ ring}dE\cos\theta
\end{equation}
We have considered the length element as point charge, it means it is very small in size and in large numbers. So here distribution of electric charge is continuous.
Put the value of dE from equ(1) to equ(3) then, we get –
\begin{equation}
E = \int_{whole\;ring}\frac{1}{4\pi\epsilon_0}.\frac{\lambda.dl}{\left(a^2+x^2\right)}\cos\theta
\end{equation}
The value of $\cos\theta$ from the figure above is given as –
$$
cos\theta = \frac{x}{r} = \frac{x}{\left(a^2+x^2\right)^{\frac{1}{2}}}
$$
Now put the value of $cos\theta$ in equ(4), we get –
\begin{equation}
E = \int_{whole\;ring}\frac{1}{4\pi\epsilon_0}.\frac{\lambda.dl}{\left(a^2+x^2\right)}\frac{x}{\left(a^2+x^2\right)^{\frac{1}{2}}}
\end{equation}
On solving this equation we get –
\begin{equation}
E = \frac{1}{4\pi\epsilon_0}.\frac{{\lambda}x}{\left(a^2+x^2\right)^{\frac{3}{2}}}\int_{whole\;ring}dl
\end{equation}
After integrating the element dl, we get 2πa, because the total lenght of the circular ring is its circumference.
\begin{align*}
\int{dq}& = \lambda\int{dl}\\
q& = \lambda{2\pi a}
\end{align*}
This is the value of total electric charge on the ring.
\begin{equation}
\begin{split}
E& = \frac{1}{4\pi\epsilon_0}.\frac{\lambda x}{\left(a^2+x^2\right)^{\frac{3}{2}}}.{2\pi a}\\
& = \frac{qx}{4\pi\epsilon_0.\left(a^2+x^2\right)^{\frac{3}{2}}}
\end{split}
\end{equation}
The direction of the net electric field intensity due to the charged ring is along the axis. And hence this the required value of electric field intensity due to a uniformly charged ring.

SPECIAL CASES

[latexpage]
1). If x>>>a then $x^2+a^2\approx x^2$, then the equation become –
\[
E = \frac{q}{4\pi\epsilon_0 x^2}
\] This formula is same as electric field intensity at distance x due to a point charge. If distance x is very large then the whole ring seems like a point charge.
2). If x = 0, means point P is lies at its centre. then E = 0.

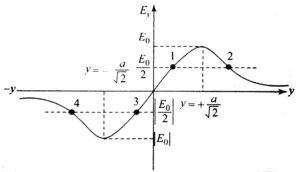
MAXIMUM ELECTRIC FIELD INTENSITY

Electric field intensity will be maximum when $\frac{dE}{dx} = 0$.
\[
\frac{d}{dx}\left[\frac{qx}{4\pi\epsilon_0.\left(a^2+x^2\right)^{\frac{3}{2}}}\right] = 0
\]
\[
\frac{q}{4\pi\epsilon_0}\left[\frac{-3x^2}{\left(a^2+x^2\right)^\frac{5}{2}}+\left(a^2+x^2\right)^\frac{-3}{2}\right] = 0
\]
\[
x = \pm\frac{a}{\sqrt{2}}
\]
The maximum electric field intensity due to a uniformly charged ring at point P is when the position of P will be at $x = \pm\frac{a}{\sqrt{2}}$.

See the graph below

Watch this video for more reference