Gauss’s Law – gauss’s law in integral form, gauss’s law in differential form

Without Gauss Theorem study of electrostatic is incomplete. So it became necessary to know about the Gauss theorem. In this article, we are going to discuss the Gauss theorem in detail. So keep reading till the end.

Gauss’s law

In electromagnetism, gauss’s law is also known as Gauss flux’s theorem. A law relates the distribution of electric charge to the resulting electric field. Gauss’s Law is mathematically very similar to the other laws of physics. Such as – gauss’s law for magnetism, gauss’s law for gravity.

However, gauss’s law can be expressed in such a way that it is very similar to the inverse square law. In physics, there are many inverse square laws, such as inverse square Coulomb’s law, inverse square Newton’s laws of gravity, inverse square magnetic Coulomb’s law, etc. Gauss’s law is essentially very equivalent or analogies to these inverse square laws.

There are two forms in which Gauss’s law can be expressed. We can express this law mathematically using vector calculus in integral form and in differential form, both forms are equivalent since they are related by the divergence theorem which is also called the Gauss theorem.

• Integral form – This form of the Gauss theorem is used when the distribution of electric charge on any closed surface is continuous or symmetrical. The integral form of Gauss law states that electric flux through any arbitrary surface is proportional to the total electric charge enclosed by the surface.
• Differential form –  This form of the Gauss theorem is used when the distribution of electric charge over a closed surface is discontinuous or unsymmetrical. The differential form of Gauss law states that the divergence of the electric field is proportional to the local density of charge.

This law was first formulated by Joseph-Louis Lagrange in 1773 and further followed by Carl Friedrich Gauss in 1813. It is one of Maxwell’s four equations. And this law can be used to derive Coulomb’s law or vice versa.

Now we are going to talk about each form of Gauss’s law in detail one by one.

Gauss law in integral form

Gauss’s law statement

The Gauss theorem states that – The surface integral of the electric field intensity over a closed surface (called Gaussian surface) in free space is equal to the $\frac{1}{\epsilon_{0}}$ times the net electric charge enclosed within the surface. Mathematically it is given as -\[
\Phi_E=\oint_{S}{E}.{dS}=\frac{1}{\epsilon_0}\sum_{i=1}^n{qi}=\frac{q}{\epsilon_0}
\]
Where ${\displaystyle{q}=\sum_{i=1}^n{qi}}$ is the algebraic sum of all the charges inside the closed surface. Hence, the total electric flux over a closed surface in a vacuum is $\frac{1}{\epsilon_{0}}$ times the total charge within the surface irrespective of how that charge is distributed.

Proof of Gauss’s laws for spherically symmetric surface

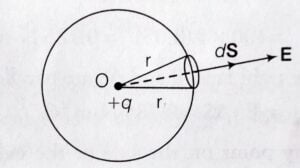
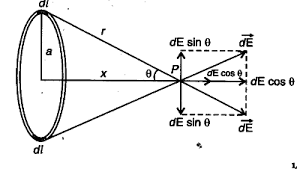
Take a $q$ charge and make a Gaussian surface of radius $r$. Now cut a small area of element $dS$ through which we will find electric flux. See figure above

The electric flux through this small symmetrical area element(surface) dS is given as –
\begin{align*}
d\phi&=E.dS=\frac{1}{4\pi\epsilon_0}\frac{q}{r^2}\hat{r}.\left(dS\hat{n}\right)\\
d\phi&=\frac{1}{4\pi\epsilon_0}\frac{qdS}{r^2}\hat{r}.\hat{n}
\end{align*}
Here, ${\displaystyle\hat{r}.\hat{n}=1.1\cos0^{\circ}=1}$, now the equation become:
$$
d\phi=\frac{1}{4\pi\epsilon_0}\frac{qdS}{r^2}
$$
The total electric flux through the spherical surface is given as-
\begin{align*}
\phi_{E}&=\oint_{S}d{\phi}\\
\phi_{E}&=\frac{1}{4\pi\epsilon_0}\frac{q}{r^2}\oint_{S}dS\\
\phi_{E}&=\frac{1}{4\pi\epsilon_0}\frac{q}{r^2}.4\pi{r^2}\\
\phi_{E}&=\frac{q}{\epsilon_0}
\end{align*}
If an electric charge is kept in a medium of dielectric constant k then-
$$
\phi_E=\frac{q}{k\epsilon_0}=\frac{q}{\epsilon_r\epsilon_0}=\frac{q}{\epsilon}
$$
Where, $\displaystyle{k=\epsilon_{r}=\frac{\epsilon}{\epsilon_0}}$
And if there is no charge enclosed in the Gaussian surface i.e q = 0 then ${\phi_E=0}$

Gauss law in differential form

Using the divergence theorem, gauss’s law can be expressed in differential form as follows:
$$
\nabla \cdot \mathbf{E} = \frac{\rho}{\varepsilon_0}
$$
where ∇ · E is the divergence of the electric field, ε0 is the electric constant also called the permittivity of the free space, and ρ is the volumetric charge density (charge per unit volume).

Equivalency of integral and differential form

Mathematically gauss laws are equivalent in integral and differential form. We can prove this equivalency by using the divergence theorem.

Equivalency proof using the Divergence theorem

The integral form of Gauss’ law is: $$ \iint_{S}{\displaystyle \mathbf {E} \cdot \mathrm {d} \mathbf {A} } = \frac{Q}{\varepsilon_0}
$$
And for any closed surface $S$ containing charge $Q$. By the divergence theorem, this equation is equivalent to:
$$
{\displaystyle \iiint _{V}\nabla \cdot \mathbf {E} \,\mathrm {d} V={\frac {Q}{\varepsilon _{0}}}}
$$
And for any volume V containing charge Q. By the relation between charge and charge density, this equation is equivalent to:
$$
{\displaystyle \iiint _{V}\nabla \cdot \mathbf {E} \,\mathrm {d} V=\iiint _{V}{\frac {\rho }{\varepsilon _{0}}}}\,\mathrm {d} V
$$
for any volume $V$. In order for this equation to be simultaneously true for every possible volume V, it is necessary for the integrands to be equal everywhere. Therefore, this equation is equivalent to:
$$
{\displaystyle \nabla \cdot \mathbf {E} ={\frac {\rho }{\varepsilon _{0}}}}
$$
Thus the integral and differential forms are equivalent.

Gauss’s law in dielectrics

Obtain the generalized form of Gauss’s law in a dielectric medium both in integral and differential forms

Gauss’s law in its general form states that the total electric flux through a closed surface is equal to the total charge enclosed by that surface divided by the permittivity of the medium. In a dielectric medium, the electric field is affected by the presence of the dielectric material, which is characterized by its relative permittivity $\varepsilon_r$.

Integral Form of Gauss’s Law in a Dielectric Medium

The integral form of Gauss’s law in a dielectric medium is given by: $$\oint_{S} \mathbf{E} \cdot \mathbf{dA} = \frac{1}{\varepsilon_{0}\varepsilon_r} \int_{V} \rho \, dV$$

Where:

• $\oint_{S}$ denotes the surface integral over a closed surface S,
• $\mathbf{E}$ represents the electric field vector,
• $d\mathbf{A}$ is a differential area vector on the closed surface,
• $\int_{V}$ represents the volume integral over the region $V$ enclosed by the closed surface,
• $\rho$ is the total charge density within $V$,
• $\varepsilon_r$ is the relative permittivity of the medium
• $\varepsilon_{0}$ is the vacuum permittivity constant $(8.854 \times 10^{-12} C^2/(N\cdot m^2))$.

Differential Form of Gauss’s Law in a Dielectric Medium

The differential form of Gauss’s law in a dielectric medium involves the divergence of the electric field vector and is given by: $$\nabla \cdot \mathbf{E} = \frac{\rho}{\varepsilon_{0}\varepsilon_{r}}$$

Where:

• $\nabla \cdot \mathbf{E}$ denotes the divergence of the electric field vector, $\rho$ represents the charge density at a given point in the medium,
• $\varepsilon_{0}$is the vacuum permittivity constant, and
• $\varepsilon_r$ is the relative permittivity of the medium

In the presence of a dielectric medium, the permittivity is multiplied by $\varepsilon r$ in both the integral and differential forms of Gauss’s law to account for the effects of the dielectric material on the electric field.

Watch the video for more reference

Applications of Gauss’s law

Till now we have discussed Gauss’s law. Now let’s What are the applications of Gauss’s law. Actually, Gauss’s laws have various applications in different fields of science and engineering. Below are given some areas where Gauss’s laws are commonly used:

1. Electrostatics: Gauss’s law for electric fields is extensively used in the study of electrostatics. It provides a convenient tool to calculate electric fields generated by charge distributions and to analyze the symmetry of electric fields around objects.
2. Magnetostatics: While Gauss’s law for magnetism states that the magnetic flux through any closed surface is zero, it is still a fundamental principle in magnetostatics. This law helps in understanding the behavior of magnetic fields and their relationship with current distributions.
3. Electromagnetism: In electromagnetism, Gauss’s law is combined with Ampere’s law to form Maxwell’s equations, which describe the behavior of electric and magnetic fields. These equations are crucial in understanding the propagation of electromagnetic waves, such as light.
4. Gravitation: Gauss’s law for gravity is used in the study of gravitational fields and their effects. It relates the gravitational flux through a closed surface to the total mass enclosed within that surface and helps in calculating the gravitational field around objects.
5. Differential Geometry: Gauss’s equations in differential geometry, also known as the Gauss-Codazzi equations, describe the intrinsic curvature of a surface embedded in higher-dimensional spaces. These equations have applications in fields such as differential geometry, general relativity, and mathematical physics.
6. Computational Physics: Gauss’s laws are often employed in numerical simulations and computational physics methods. They provide a basis for discretizing equations and solving physical problems numerically.

Frequently Asked Questions – FAQs