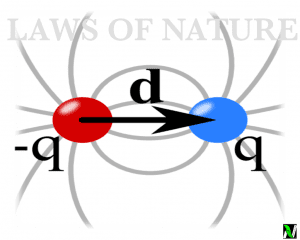
ELECTRIC FIELD INTENSITY DUE TO A SHORT ELECTRIC DIPOLE

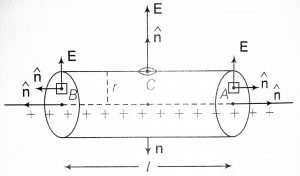
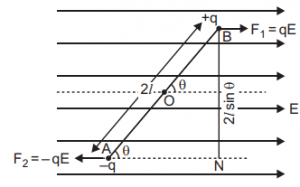
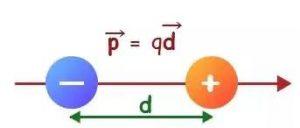
Let’s a take a short dipole having +q charge at point A and -q charge at point B and which is seperated by the distance 2l and where O is the centre of the dipole.

Now let’s take any point P at distance r from the centre O, in the three dimensional space around the dipole  where electric field intensity is to be found. Join the point P to O. After joining the line from point P to the centre of the dipole O. You will see that the PO line is inclined to the line OB. Let’s take angle of inclination as θ.

Now we are interested in finding the electric field intensity due to this short electric dipole at point P which is inclined at angle θ. Umm! But wait…

This problem is not same as to finding electric field intensity at axial or equatorial line, this is somehow different from that.

We have to do some construction in order to find the value of electric field at point P. Draw a dotted line between A2 and B2 such that it’s become perpendicular to the line OP. This dotted line is nothing but it is the dipole same as dipole AB. After constructing the line A2B2, the point P seems to be lie on the equatorial line of OP.

Now draw a dotted line between A1 and B1 such that it become axial to the line OP. After constructing the line between A1 and B1 the point P seems to be lie on the axial line of OP.

There are two electric field intensity are present at point P. One is the electric field intensity at the point P on the axial line and the second is the electric field intensity at the point P on the equatorial line.

On resolving this electric field intensity in two components it breaks into PN and PM as shown in the following figure. PN show the axial electric field (E1) and PM show the equatorial electric field (E2). The resultant electric field intensity goes through the line PQ.

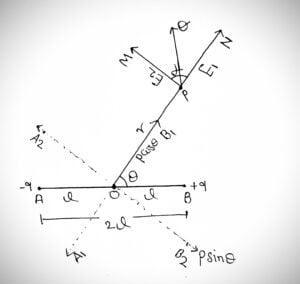
Now we are going to derive an expression for electric field intensity at any point around the dipole which is inclined at angle θ on the dipole AB.

DERIVATIONS FOR ELECTRIC FIELD INTENSITY AT POINT P DUE TO SHORT DIPOLE

[latexpage]
Electric field intensity due to a short dipole at point P on the axial line is –
\begin{equation}
E_{axial} = \frac{1}{4\pi\epsilon_0}\frac{2p\cos\theta}{r^3}
\end{equation}
And the electric field intensity due to a short dipole at point P on the equatorial line is –
\begin{equation}
E_{equatorial} = \frac{1}{4\pi\epsilon_0}\frac{p\sin\theta}{r^3}
\end{equation}
Resultant electric field intensity E is given as :
\begin{equation}
E = \sqrt{E_1^2 + 2E_1E_2\cos\phi + E_2^2}
\end{equation}
Put the value of $E_1$ and $E_2$ in eqs …….(3)
\begin{equation}
E = \sqrt{\left(\frac{1}{4\pi\epsilon_0}\frac{2p\cos\theta}{r^3}\right)^2 + \left(\frac{1}{4\pi\epsilon_0}\frac{p\sin\theta}{r^3}\right)^2}
\end{equation}
The term $2E_1E_2\cos\phi$ become zero because φ is 90°
On solving this equation we get –
\begin{equation}
E = \frac{p}{4\pi\epsilon_0.r^3}\sqrt{3\cos^2\theta + 1}
\end{equation}
This is the required value of electric field intensity due to a short dipole placed at any point P in the three dimensional space.

SPECIAL CASES :

From the knowledge of electric field intensity due to a short dipole placed at any point P in three dimensional space. We can derive the expression of electric field intensity for point on the axial line and the for the point on the equatorial line. Which is as follows :

FOR AXIAL LINE

[latexpage]
Derived electric field equation is –
\begin{equation}
E = \frac{p}{4\pi\epsilon_0.r^3}\sqrt{3\cos^2\theta + 1}
\end{equation}
We know that in axial line angle between point P and dipole is 0°, so cos0 = 1
\begin{equation}
E = \frac{p}{4\pi\epsilon_0.r^3}\sqrt{3 + 1}
\end{equation}
Now it’s become
\begin{equation}
E = \frac{2p}{4\pi\epsilon_0.r^3}
\end{equation}
This is the required value of electric field intensity at axial point.

FOR EQUATORIAL LINE

[latexpage]
Derived equation is given as –
\begin{equation}
E = \frac{p}{4\pi\epsilon_0.r^3}\sqrt{3\cos^2\theta + 1}
\end{equation}
We know that in equatorial line the angle between the point P and the dipole is 90°, so cos90° = 0
\begin{equation}
E = \frac{p}{4\pi\epsilon_0.r^3}\sqrt{0 + 1}
\end{equation}
Now the equation become –
\begin{equation}
E = \frac{p}{4\pi\epsilon_0.r^3}
\end{equation}
This is the required value of electric field intensity at the equatorial point.