Gauss’s law class 12: statement, applications, formula derivations

So far we have learned about Gauss’s law class 12 in detail. In this article, we are going to talk about the application of Gauss’s law. So keep reading till the end.

We know that Gauss’s law is a law that relates the distribution of electric charge to the resulting electric field. This means we can find the value of the electric field by using Gauss’s law.

Yes, we can find the value of the electric field by using Gauss’s Law, because it gives the relationship between the electric field and the total charge enclosed. Gauss’s Law makes the calculation of electric field very easy because it is approximately free of tough integration and long processes. Gauss’s law is very useful in finding an electric field of such charge containing symmetrical objects whose electric field cannot be found by using a simple formula of the electric field.

There are many cases where Gauss law can be used for finding an electric field, but here, we will talk about only three famous cases i.e

• Electric field due to an infinitely long straight charged wire.
• Electric field due to a thin infinitely charged plane sheet.
• Electric field due to the uniformly charged thin spherical shell.

Before applying Gauss’s law. We should learn, how is Gauss’s law used. Gauss law can be used in the following way –

• Make a symmetrical Gaussian surface that enclosed all the charges.
• It is not necessary that the Gaussian surface coincides with the actual surface of the charged body. It can be inside or outside of the Gaussian surface.

Before going ahead and start discussing applications of Gauss’s law, let’s recall what is Gauss’s law once again.

What is Gauss’s law, class 12?

Imagine you have a magical power to create electric fields. You can create electric fields around any charged object, like a balloon or a metal rod. Now, let’s say you want to know how these electric fields behave and how they interact with charges. This is where Gauss’s law comes into play.

Gauss’s law is like a detective tool for electric fields. It helps us understand how electric fields are generated and how they spread out in space. One of the coolest things about Gauss’s law is that it connects the electric field with the charges that create it.

Here’s the deal: Gauss’s law states that the total electric flux passing through a closed surface is directly proportional to the total charge enclosed by that surface. Flux is like a measure of how many electric field lines pass through a given area. So, if you have a lot of electric field lines passing through a surface, it means there’s a lot of charge inside that surface.

Think of it this way: Imagine you have a balloon filled with electric field lines. When you squeeze the balloon, you’re reducing the surface area, right? Well, according to Gauss’s law, if you squeeze the balloon and decrease the surface area, the number of electric field lines passing through that surface will decrease as well. It’s like squeezing the balloon and pushing some of the electric field lines out.

Gauss’s law also takes into account the strength of the electric field. It tells us that the flux passing through a surface is equal to the total charge enclosed divided by a constant called vacuum permittivity. This constant essentially tells us how “easy” it is for electric field lines to spread out or squeeze together.

So, Gauss’s law helps us understand the relationship between charges and electric fields. It tells us that the electric field lines are like detectives, pointing towards the charges that create them. It allows us to calculate the electric field by looking at the charges enclosed by a surface. And it’s not just a dry equation; it’s a magical connection that reveals the invisible forces of electricity and charges.

Next time you see a spark, remember that behind it lies the fascinating world of electric fields and Gauss’s law, helping us unlock the mysteries of charged particles and their interactions.

Gauss’s law statement

Gauss’s law statement: “Gauss’s law states that the total electric flux passing through any closed surface is proportional to the total electric charge enclosed by that surface.” Mathematically, it can be expressed as:

$$\Phi_E=\oint_{S}{E}.{dS}=\frac{1}{\epsilon_0}\sum_{i=1}^n{qi}=\frac{q}{\epsilon_0}$$

Where ${\displaystyle{q}=\sum_{i=1}^n{qi}}$ is the algebraic sum of all the charges inside the closed surface. Hence, the total electric flux over a closed surface in a vacuum is $\frac{1}{\epsilon_{0}}$ times the total charge within the surface irrespective of how that charge is distributed.

In other words, the electric flux (a measure of how many electric field lines pass through a given area) passing through a closed surface is directly related to the total electric charge contained within that surface. If there is a greater amount of electric charge inside the surface, more electric field lines will pass through, resulting in a larger electric flux.

Gauss’s law provides a fundamental connection between electric fields and the charges that generate them. It helps us understand how electric fields spread out from charged objects and how the distribution of charges influences the electric field around them. By applying Gauss’s law, we can analyze the behavior of electric fields and calculate their strength in different situations.

Remember, Gauss’s law is like a powerful detective tool that unveils the hidden relationship between charges and electric fields.

Applications of Gauss’s law

Now let’s discuss the applications of Gauss’s law. In this article, we will primarily discuss three applications of Gauss’s law as per the CBSE class 12 physics. These three applications are:

• Electric field due to an infinitely long straight charged wire.
• Electric field due to a thin infinitely charged plane sheet.
• Electric field due to the uniformly charged thin spherical shell.

Now, discussed each of them one by one.

Electric field due to an infinitely long charged wire

Consider an infinitely long thin straight charged wire of uniform linear charged density ($\lambda$). See figure below

From the symmetry, the electric field is everywhere radial the plane cutting the wire normally and its magnitude depends on the radial distance r.
From the knowledge of Gauss law-
\begin{align*}
\phi_{E}&=\oint_{S}E.{d{S}}=\frac{q}{\epsilon_0}\\
&=\oint_{S}E.{d{S}}=\oint_{S}E.\hat{n}{d{S}}\\
&=\oint_{A}E.\hat{n}{d{S}}+\oint_{B}E.\hat{n}{d{S}}+\oint_{C}E.\hat{n}{d{S}}
\end{align*}
Now solving further, we get-
\begin{align*}
\oint_{S}E.{d{S}}&=\oint_{A}E.{d{S}}\cos{90}\\
& +\oint_{B}E.{d{S}}\cos{90}+\oint_{C}E.{d{S}}\cos{0}\\
\oint_{C}E.{d{S}}&=E\left(2\pi{r}{l}\right)
\end{align*}
The charge enclosed in the cylinder,${\displaystyle{q=\lambda{l}}}$
\begin{align*}
E\left(2\pi{r}{l}\right)&=\frac{\lambda{l}}{\epsilon_{0}}\\
E&=\frac{\lambda}{2\pi\epsilon_0{r}}
\end{align*}
The direction of the electric field is radially outward from the positive line charge but if the line charge is negatively charged then the electric field is radially inward.
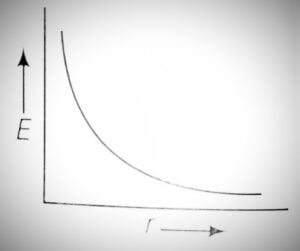
Thus, the electric field (E) due to the linear charge is inversely proportional to the distance (r). The variation of the electric field (E) with distance (r) is shown in the figure below.

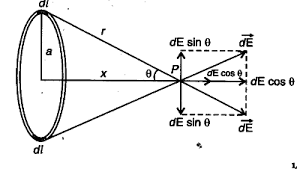
Electric field due to an infinitely thin charged plane sheet

Let’s consider $\sigma$ to be the surface charge density of a plane-charged sheet. From the symmetry, E will be on either side of the sheet and must be perpendicular to the plane of the sheet. The electric field (E) will be the same in magnitude at all the points equidistant from the plane sheet.

Take a cylinder of cross-sectional area A and length 2r as Gaussian surface. See the figure below:

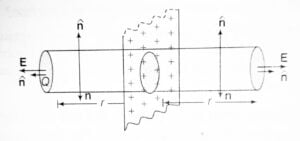
On the curved surface of the cylinder, the electric field (E) and $\hat{n}$ are perpendicular to each other. Therefore, the electric flux through the curved surface is zero.
Flux through the flat surfaces is given as-
$$
{E}{A}+{E}{A}=2{E}{A}
$$
Therefore, the total electric flux through the entire cylindrical surface is –
$$
\phi_{E}=2{E}{A}
$$
The total electric field enclosed by the cylindrical surface is –
$$
q=\sigma{A}
$$
According to Gauss’s law, we have –
\begin{align*}
\phi_{E}&=\frac{q}{\epsilon_0}\\
2{E}{A}&=\frac{\sigma{A}}{\epsilon_{0}}\\
E&=\frac{\sigma}{2\epsilon_{0}}
\end{align*}
Here, you can see that, the electric field is independent of r, the distance of the point from the plane charged sheet.
It means that electric field intensity remains the same at all points close to the charged plane sheet. The electric field is directed away from the plane sheet if it is positively charged or if it is negatively charged then the electric field is directed inward.

Read Also

• Gauss law for magnetism class 12 | statement, derivation, differential form, and integral form
• Gauss’s Law – gauss’s law in integral form, gauss’s law in differential form
• Electric Charges, types, units, and properties
• Superposition principle | electric field due to system of Charges.

Electric field due to a uniformly charged thin spherical shell

Let’s consider $\sigma$ to be the surface charge density of a thin spherical shell of radius R. The Gaussian surface is also a spherical surface of the center same as of the shell. See the figure below:

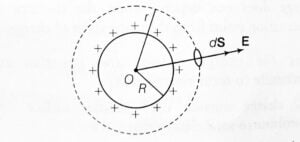
1). At a point outside the shell, (r>R)

From the figure, $E$, and $dS$ are in the same direction. Therefore, electric flux is given as-
$$
\phi_{E}=\oint_{S}E.{d{S}}=\frac{q}{\epsilon_{0}}
$$
Further solving, we get-
\begin{align*}
\phi_{E}&=E\oint_{S}{d{S}}=\frac{q}{\epsilon_{0}}\\
E\left(4\pi{r^2}\right)&=\frac{q}{\epsilon_{0}}\\
E&=\frac{q}{4\pi\epsilon_{0}{r^2}}
\end{align*}
The total electric charge on the spherical shell and the further solution is-
\begin{align*}
q&=\sigma\times{4\pi{R^2}}\\
E&=\frac{\sigma{R^2}}{\epsilon_{0}{r^2}}\\
\end{align*}
Vectorially, $\displaystyle{E=\frac{\sigma{R^2}}{\epsilon_{0}{r^2}}}\hat{r}$

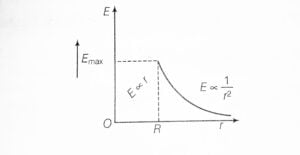
2). At a point on the surface of the shell (r=R)

If the point is on the surface of the shell, then the radius of the Gaussian surface and the radius of the shell is equal, (r = R), then the value of the electric field is-
$$
E=\frac{\sigma}{\epsilon_0}
$$

3). At the point inside the shell,(r<R)

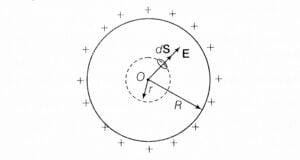
If the point is inside the shell, then there is no charge enclosed by the Gaussian surface. You can see this in the above figure. It means $q = 0$, and this gives, $E = 0$.
The variation of electric field intensity with distance from the center of the uniformly charged spherical shell is shown in the figure below.

Frequently Asked Questions – FAQs