WHEATSTONE BRIDGE

An electrical bridge was invented by Samuel Hunter Christie in 1833 and further this electrical circuit bridge was enhanced and popularized by Sir Charles Wheatstone in 1843.

For enhancing and popularizing this bridge, it was named Wheatstone bridge in Charles Wheatstone’s honor. Initially, this bridge was used for soil analysis and comparison. But further, it is being used for the measurement of the unknown resistance.

So what is the Wheatstone bridge? What is its working principle? What is its construction? How is it used for the measurement of unknown resistance? We will discuss everything in this article, so let’s start…

WHAT IS WHEATSTONE BRIDGE?

Wheatstone bridge is a quadrilateral-shaped electrical circuit, which is used to measure unknown resistance by balancing two legs of the circuit. In one leg there exists an unknown resistance, whose value we want to find. The good thing is that it gives very accurate measurements when balanced conditions are met.[latexpage]

In the above figure, $\displaystyle{R_{x}}$ is the unknown resistance. But the resistance $\displaystyle{R_{1}}$ and $\displaystyle{R_{3}}$ have fixed value of resistance and their resistance value has been given.

Whereas $\displaystyle{R_{2}}$ is an adjustable resistor, we can adjust its resistance value according to our need.

Between points, B and D there exist a galvanometer that measures the presence of electric current in the arm BD. If the galvanometer detects no currents in the arm BD then we say –  it is a balanced Wheatstone bridge.

At this balanced point, this bridge shows a unique behavior. At these balanced conditions, the ratio of resistance in the arm CD and DA is equal to the ratio of resistance in the arm BC and CA.

CONSTRUCTION OF THE WHEATSTONE BRIDGE

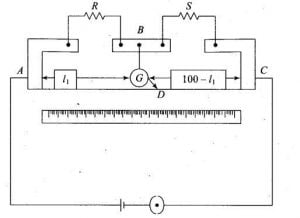
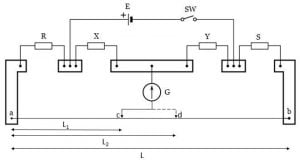
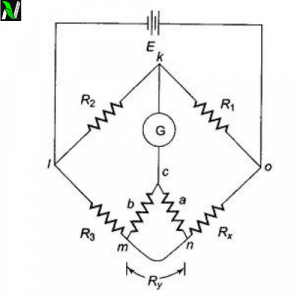
The construction of the Wheatstone bridge is very simple. You only need two known resistances (labeled them $\displaystyle{R_{1}}$ and $\displaystyle{R_{3}}$), a variable resistor $\displaystyle{R_{2}}$ (whose value can be changed as per our choice), an unknown resistance $\displaystyle{R_{x}}$ (the resistance whose value you willing to find) and a galvanometer and a source.

Connect $\displaystyle{R_{1}}$ and $\displaystyle{R_{2}}$ in series and similarly connect $\displaystyle{R_{3}}$ and $\displaystyle{R_{x}}$ series. Then joined their terminals to the point A and C, as you joined their terminals to the point A and C, this two series resistance aligned to form a parallel combination.

When you stretch the point Band D outwardly then you will see a four-sided quadrilateral. Now connect the galvanometer to points B and D as shown in the figure above. The galvanometer helps us to be sure that the bridge is in a balanced condition or not.

Finally, connect the power source to the bridge. For this join cathode of the source to point A and anode to the point C as shown in the figure above, but you can join cathode or anode to any points either A or C, it’s all your choice.

WORKING PRINCIPLE

When we supply power to this bridge, then this bridge starts working. But it works like a simple circuit until it doesn’t get balanced.

We know that, in this bridge $\displaystyle{R_{1}}$, $\displaystyle{R_{2}}$ and $\displaystyle{R_{3}}$ are known resistance in which  $\displaystyle{R_{2}}$ is adjustable. The resistance $\displaystyle{R_{2}}$ helps us to attend the stability of this bridge by adjusting it’s value.

The resistance $\displaystyle{R_{2}}$ is adjusted until the bridge is getting balanced such that no current flows through the galvanometer V_g. At this point, when there is no current flowing through the galvanometer then the potential difference between the two midpoints (B and D) will be zero, and the galvanometer shows null deflection. This is the underlying principle behind the working of the Wheatstone bridge.

So at this balanced or stable condition, the ratio of the two resistances in the known leg (R₂ / R₁) is equal to the ratio of the two resistances in the unknown leg (R_x / R₃). But if the bridge is unbalanced, then the direction of the electric current indicates whether the value of the $\displaystyle{R_{2}}$ is too high or too low. If R₁, R₂, and R₃ are known, but R₂ is not adjustable, then the potential difference across or current flow through the galvanometer can be used to calculate the value of $R_x$ by using Kirchhoff’s circuit laws.

At the balanced condition –
\begin{align*}
\frac{R_{2}}{R_{1}}&=\frac{R_{x}}{R_{3}}\\
\implies\qquad R_{x}&=\frac{R_{2}}{R_{1}}.R_{3}
\end{align*}

Detecting zero current in the galvanometer is a work of very high precision. If $R_1$, $R_2$, and $R_3$ are known to high precision, then $R_x$ can be measured to the high precision. A very small change to the $R_x$ can disturb the stability of the Wheatstone bridge and it can be easily detected by the galvanometer.

DERIVATION FOR WHEATSTONE BRIDGE

USING BALANCED CONDITION

If the Wheatstone bridge is in a balanced condition then both the potential difference and current across the galvanometer (point B and D) will be zero. If this happens then it will be ${\displaystyle I_{1}=I_{2}}, {\displaystyle I_{3}=I_{x}}, {\displaystyle V_{D}=V_{B}}$, so from this-
\begin{align*}
\frac{V_{DC}}{V_{AD}}&=\frac{V_{BC}}{V_{AB}}\\
\frac{I_2R_2}{I_1R_1}&=\frac{I_xR_x}{I_3R_3}\\
\implies\qquad R_{x}&=\frac{R_{2}}{R_{1}}.R_{3}
\end{align*}

This is the simplest proof or derivation of the Wheatstone bridge.

USING KIRCHHOFF’S CIRCUIT LAWS

So, we can also find the value of $R_x$ by using Kirchhoff’s circuit law. To find the value of $R_x$ by Kirchhoff’s law. Lets first apply Kirchhoff’s junction rule at the point B and D –
\begin{align*}
I_3+I_G-I_x&=0\\
I_1-I_2-I_G&=0
\end{align*}
Now apply Kirchhoff’s voltage law in the loops ABDA and BCDB to find the value of voltage:
\begin{align*}
(I_3 \cdot R_3) – (I_G \cdot R_G) – (I_1 \cdot R_1) &= 0 \\
(I_x \cdot R_x) – (I_2 \cdot R_2) + (I_G \cdot R_G) &= 0
\end{align*}
If the bridge is balanced, then $I_G=0$ so we can rewrite the second set of equations as-
{\displaystyle {\begin{align*}I_{3}\cdot R_{3}&=I_{1}\cdot R_{1}\quad {\text{(1)}}\\I_{x}\cdot R_{x}&=I_{2}\cdot R_{2}\quad {\text{(2)}}\end{align*}
Now divide the equ(1) by equ(2) then, after dividing we get-
$$
R_x = {{R_2 \cdot I_2 \cdot I_3 \cdot R_3}\over{R_1 \cdot I_1 \cdot I_x}}
$$
If the bridge is balanced then $I_G$ must be zero, if $I_G$ is equal to zero then from Kirchhoff’s current law above, $I_3=I_x$ and $I_2=I_1$, so $I_3I_2$ over $I_1I_x$ will get canceled out from the above equation, then we get-
$$
R_{x}=\frac{R_{2}}{R_{1}}.R_{3}
$$

SIGNIFICANCE OF WHEATSTONE BRIDGE

Sometimes Wheatstone bridge illustrates the idea of measuring the different quantities very accurately. The variations in the Wheatstone bridge can be used to measure capacitance, inductance, impedance, and many other quantities. The kelvin bridge is the small adaptation of the Wheatstone bridge, which is used to find the value of very small resistance.

In many cases, measuring the unknown resistance is related to measuring some physical factors such as temperature, pressure, force, etc. so thereby it allows to use of the Wheatstone bridge to find those elements values indirectly.

MODIFICATIONS IN WHEATSTONE BRIDGE

Wheatstone bridge is the fundamental bridge, it is basically used to find the known resistance. But physicists have carried out several modifications in this bridge to find the different kinds of resistance, where the fundamental Wheatstone bridge is not suitable for use. Some of the modifications are given below-

• Carey Foster bridge is used to measuring small resistances
• Kelvin bridge is used for measuring small four-terminal resistances
• Maxwell bridge and Wien bridge is used for measuring reactive components
• Anderson’s bridge is used for measuring the self-inductance of the circuit, an advanced form of Maxwell’s bridge

ERRORS IN WHEATSTONE BRIDGE

Some basic error which can be occurred in the measurements of the unknown resistance by using Wheatstone bridge is listed below –

• The difference between the true and the marked value of the three resistance can give errors in measurements.
• The use of bad quality galvanometer in the Wheatstone bridge can lead to inaccuracy in balanced points.
• self-heating of the resistance can increase its resistance and results can give different measurements.
• The personal error can occur in the galvanometer by taking the reading at the null point.
• The bad setup of the Wheatstone bridge can rises errors in measurements.

Stay tuned with Laws Of Nature for more useful and interesting content.