Note: some equations can go out of your mobile screen. Please use landscape or desktop mode to view the complete equations.

KELVIN BRIDGE OR KELVIN DOUBLE BRIDGE

INTRODUCTION

We are acquainted with Wheatstone bridge. Do we know that what is Wheatstone bridge? And why it is used for? Wheatstone bridge is a quadrilateral-shaped electrical circuit device, which is used to obtain the electrical resistance of unknown resistors when the galvanometer shows null deflection.

Suggested reading: Wheatstone bridge

But can the Wheatstone bridge be used to calculate the value of any type of resistance? Perhaps not, because it has its own limitations. Wheatstone bridge is used to find the value of such Resistors whose resistance value is above 1Ω.

It can measure electrical resistance ranges few ohms to several ohms accurately. This can not be used to find every type of electrical resistance. When the Wheatstone bridge is used to find the electrical resistance below one ohm, it shows significant errors.

So to overcome this error, a new circuit device is used to find the value of lower resistance that is called kelvin bridge. In this article, we are going to discuss everything about the kelvin bridge, so let’s start…

WHY DO WE NEED KELVIN BRIDGE?

Before we explain, why do we need a kelvin bridge? let’s take a look at three important ways to categorize electrical resistance.

1. High Resistance: Resistance that is greater than 0.1 Mega-ohm.
2. Medium Resistance: Resistance that ranges from 1 ohm to 0.1 Mega-ohm.
3. Low Resistance: Resistance value that is lower than 1 ohm.

The main purpose behind categorizing this electric resistance is that you can understand that, in electrical engineering, every gadget or device has its own specific functions with a definite range.

If you want to measure the resistance of each category then you would need three different devices to measure them. You can’t measure the resistance of each category with only a Wheatstone bridge or ohm-meter.

It means if a device that measures high resistance with high accuracy doesn’t mean that it also measures low or medium resistance with the same high accuracy.

So for the resistance which is lower than one ohm, we use a special type of bridge called kelvin bridge for measurement of their electric resistance because, for the resistors which are less than one ohm, the resistance of the connecting wires or terminals becomes significant, so in this case, Wheatstone bridge failed to measure accurate resistance.

But when we measure resistance more than one ohm then the resistance of the connecting wires or terminals is negligible compared to the resistance value. So here Wheatstone bridge is a good choice to find the resistance of unknown resistance.

So hope you understand the need for the kelvin bridge.

WHAT IS KELVIN BRIDGE?

DEFINITION

Kelvin bridge or kelvin double bridge and in some countries called Thomson bridge is a circuit device used to measure the resistance lower than one ohm. [latexpage]

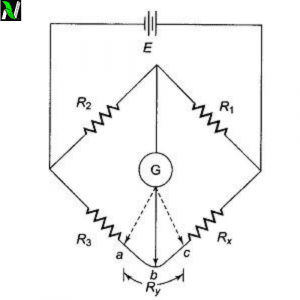
It is a modified version of the Wheatstone bridge. It is obtained, when we modify the portion where the galvanometer joined the arm which contains the unknown resistance $R_{x}$, see figure below:

DERIVATION FOR BALANCED EQUATION OF KELVIN BRIDGE

Let’s consider the circuit above, in the above circuit, $R_y$ represents the resistance of the connecting wire from R₃ to R_x (unknown resistance). Thegalvanometercan can be connected either to point c or to point a.

When it is connected to point a the resistance R_y of the connecting wire is added to the unknown resistance R_x and resulting, it increases the resistance of the R_x.

But when the galvanometer is connected to point c, then the resistance $R_y$ is added to the resistance (bridge arm) R_3, and resulting, in a lower resistance of R_x than the actual value.

But if we connect the galvanometer to point b, in between the points a and c, in such a way that the ratio of the resistance of b to c and that of a to b equals the ratio of resistances R₁ and R₂, then-
\begin{equation}
\frac{R_{bc}}{R_{ab}}=\frac{R_1}{R_2}
\end{equation}
Balanced equation of the bridge when the galvanometer is joined to the intermediate position b.
\begin{equation}
\begin{split}
\left(R_x+R_{bc}\right)=\frac{R_1}{R_2}&\left(R_3+R_{ab}\right)\\
R_{ab}+R_{cb}=R_y \quad \text{and}\quad\frac{R_{bc}}{R_{ab}}&=\frac{R_1}{R_2}\\
\frac{R_{bc}}{R_{ab}}+1&=\frac{R_1}{R_2}+1\\
\frac{R_{bc}+R_{ab}}{R_{ab}}&=\frac{R_1+R_2}{R_2}\\
i.e\qquad \frac{R_y}{R_{ab}}&=\frac{R_1+R_2}{R_2}\\
Therefore\qquad R_{ab}&=\frac{R_2R_y}{R_1+R_2}\\
\text{and as}\; R_{ab}&+R_{cb}=R_y\\
R_{cb}=R_y-R_{ab}\implies\;& R_y-\frac{R_2R_y}{R_1+R_2}\\
R_{cb}=\frac{R_1R_y+R_2R_y-R_2R_y}{R_1+R_2}&=\frac{R_1R_y}{R_1+R_2}
\end{split}
\end{equation}
Substituting the value of $R_{ab}$ and $R_{cb}$ in the above equation, then we have-
\begin{equation}
\begin{split}
R_x+\frac{R_1R_y}{R_1+R_2}&=\frac{R_1}{R_2}\left(R_3+\frac{R_2R_y}{R_1+R_2}\right)\\
R_x+\frac{R_1R_y}{R_1+R_2}&=\frac{R_1R_3}{R_2}+\frac{R_1R_2R_y}{R_2(R_1+R_2)}\\
\implies \qquad R_x&=\frac{R_1R_3}{R_2}
\end{split}
\end{equation}
The result of equation (3) is the standard Wheatstone’s balance equation. It shows that the effect of the resis­tance of the connecting wire from point a to point c has been eliminated by connecting the galvanometer to an intermediate position point b.

KELVIN DOUBLE BRIDGE

The principle which we have discussed above forms the basis of the construction of Kelvin’s Double Bridge also called Kelvin’s Bridge. It is called a Double bridge because it adds up the second set of ratio arms. See figure below:

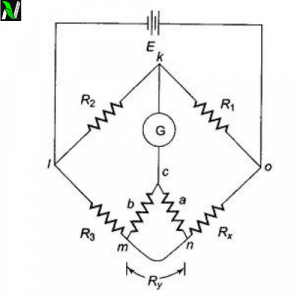
In the figure above, you can see that the second set of resistance arm, a and b is connected to the galvanometer at point c and it is also connected to the point m and n at the appropriate potential between them to eliminate the lead resistance $R_y$.

They are connected in such a way that the ratio of the resistances of arms a and b is equal to the ratio of $R_1$ and $R_2$. When the potentials at k and c are equal then the galvanometer show null deflection. See the balanced equation for the kelvin double bridge.
\begin{equation}
\begin{split}
E_{lk}&=E_{lmc}\\
E_{lk}&=\frac{R_2}{R_1+R_2}\times E\\
E&=I\left(R_3+R_x+\frac{\left(a+b\right)R_y}{a+b+R_y}\right)
\end{split}
\end{equation}
Put the value of E in the above equation (4), then, it becomes-
\begin{equation}
\begin{split}
E_{lk}&=\frac{R_2}{R_1+R_2}\times I\left[R_3+R_x+\frac{\left(a+b\right)R_y}{a+b+R_y}\right]\\
E_{lmc}&=I\left[R_3+\frac{b}{a+b}\left\lbrace\frac{\left(a+b\right)R_y}{a+b+R_y}\right\rbrace\right]\\
\text{So we have}&\quad E_{lk}=E_{lmc}
\end{split}
\end{equation}
Equating the value of$\displaystyle{E_{lk}\;\text{and}\;E_{lmc}}$, then we get-
\begin{equation}
\begin{split}
i.e\qquad \frac{IR_2}{R_1+R_2}\left(R_3+R_x+\frac{\left(a+b\right)R_y}{a+b+R_y}\right)&=I\left[R_3+\frac{b}{a+b}\left\lbrace\frac{\left(a+b\right)R_y}{a+b+R_y}\right\rbrace\right]\\
R_3+R_x+\frac{\left(a+b\right)R_y}{a+b+R_y}&=\frac{R_1+R_2}{R_2}\left[R_3+\frac{bR_y}{a+b+R_y}\right]\\
R_3+R_x+\frac{\left(a+b\right)R_y}{a+b+R_y}&=\left(\frac{R_1}{R_2}+1\right)\left[R_3+\frac{bR_y}{a+b+R_y}\right]\\
\end{split}
\end{equation}
On further solving, we get-
\begin{equation}
\begin{split}
R_3+R_x+\frac{\left(a+b\right)R_y}{a+b+R_y}&=\frac{R_1R_3}{R_2}+R_3+\frac{bR_1R_y}{R_2\left(a+b+R_y\right)}+\frac{bR_y}{\left(a+b+R_y\right)}\\
R_x&=\frac{R_1R_3}{R_2}+\frac{bR_1R_y}{R_2\left(a+b+R_y\right)}+\frac{bR_y}{\left(a+b+R_y\right)}-\frac{\left(a+b\right)R_y}{a+b+R_y}\\
R_x&=\frac{R_1R_3}{R_2}+\frac{bR_1R_y}{R_2\left(a+b+R_y\right)}+\frac{bR_y-aR_y-bR_y}{a+b+R_y}\\
R_x&=\frac{R_1R_3}{R_2}+\frac{bR_1R_y}{R_2\left(a+b+R_y\right)}-\frac{aR_y}{a+b+R_y}\\
R_x&=\frac{R_1R_3}{R_2}+\frac{bR_y}{\left(a+b+R_y\right)}\left(\frac{R_1}{R_2}-\frac{a}{b}\right)\\
&\text{But we know that,}\qquad\frac{R_1}{R_2}=\frac{a}{b}\\
\text{Therefore,}\qquad R_x&=\frac{R_1R_3}{R_2}
\end{split}
\end{equation}
This is the standard equation for Kelvin’s Bridge theory. It indicates that the resistance of the connecting wire/lead has no effect on the measurement if the ratios of the resistances of the two sets of ratio arms are equal. In a typical Kelvins Bridge theory, the range of a resistance covered is 1 — 0.00001 Ω (10 μohm) with an accuracy of ± 0.05% to ± 0.2%.

ADVANTAGES OF KELVIN BRIDGE

Some advantages of the Kelvin bridge is listed below:

• It can measure resistance value in the range of 10μΩ to 1μΩ with the accuracy of ± 0.05% to ± 0.2%.
• It consumes less power.
• Construction is a simple one, not very complex.
• Its sensitivity is high.

DISADVANTAGES OF KELVIN BRIDGE

Some disadvantages of the Kelvin bridge is listed below:

• The galvanometer is used to check whether the bridge is balanced or not.
• A high current is required to obtain good sensitivity of the bridge.
• Manually adjustments are made to obtain the null point. This process consumes a lot of time.

Stay tuned with Laws Of Nature for more useful and interesting content.